Подобие тепловых процессов

Критерии подобия тепловых процессов вводятся из уравнения Фурье – Кирхгофа:

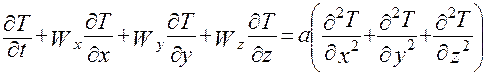(2.113)

Для полного описания конвективного переноса теплоты необходимо присоединить к уравнению Фурье – Кирхгофа уравнения Навье – Стокса и неразрывности, а также алгебраическое уравнение зависимости вязкости от температуры.

Преобразуем уравнение Фурье – Кирхгофа формальным, но простым способом: отбрасывая знаки математических операторов:

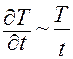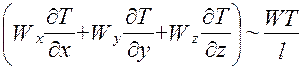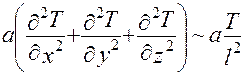(I) (II)

(III)

Далее, разделив одну часть уравнения на другую, находим критерии подобия:

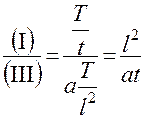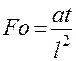; – Критерий Фурье (2.114)

Критерий Фурье характеризует распространение теплоты теплопроводностью при изменении температуры во времени, является аналогом критерия гомохронности Ho.

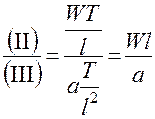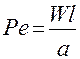; – Критерий Пекле (2.115)

Критерий Пекле характеризует соотношение между интенсивностью переноса теплоты конвекцией и теплопроводностью в движущемся потоке.

Рассмотрим подобие граничных условий.

Тепловой поток на границе раздела фаз можно выразить с помощью уравнения Фурье:

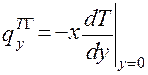(2.116)

Тот – же поток можно выразить в виде линейной зависимости от разности 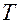на границе и в ядре потока жидкости :

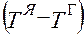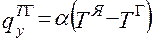(2.117)

Здесь 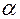– коэффициент теплоотдачи. Тогда получим:

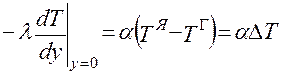(2.118)

Проведя формальное преобразование (2,118) имеем:

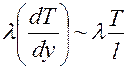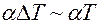(I) (II)

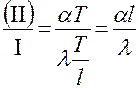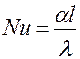; – Критерий Нуссельта (2.119)

Критерий Нуссельта характеризует отношение суммарного переноса теплоты конвекцией и теплопроводностью (т.е. теплоотдачей) к теплоте, передаваемой теплопроводностью.

Для подобия процессов теплообмена необходимо:

, ,

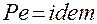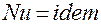
Кроме того, необходимым условием подобия процессов переноса теплоты является соблюдение гедродинамического подобия. Тогда критериальное уравнение теплоотдачи имеет вид:

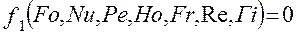(2.120)

или

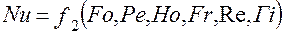(2.121)

Критерий Эйлера в уравнение не вошёл, т.к. 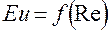. Преобразования критерия Пекле дают:

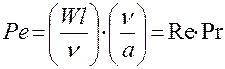(2.122)

Критерий Прандтля 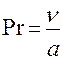– характеризует подобие физических свойств теплоносителей. Для газов 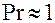, жидкостей ÷.

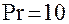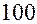Для установившегося процесса теплообмена:

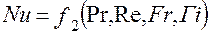(2.123)

При вынужденной теплоотдаче критерием Fr можно пренебречь:

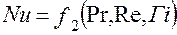(2.124)

Обычно критериальное уравнение представляют в виде степенной зависимости:

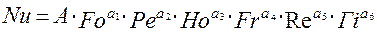(2.125)

Здесь 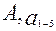– экспериментально найденные коэффициенты.

Дата добавления: 2014-01-14