Элементы гидравлики

Лекция 5.

Тема: Элементы гидравлики для одномерного течения несжимаемой жидкости.

Рассматриваем одномерное стационарное течение несжимаемой жидкости без теплообмена. При этом нет необходимости рассматривать уравнение энергии, достаточно уравнения баланса механической энергии в интегральном виде (интеграла Бернулли):

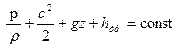
и уравнения неразрывности в виде:

.

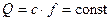При этом возникает вопрос, как описать потери трения?

Модели трения в одномерном движении вводятся, в некотором смысле, искусственно: трение в жидкости связано с производной скорости по нормали 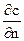. Но в одномерном течении поперек направления движения, по живому сечению скорость не меняется, 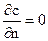, и трения нет!

Для разрешения этого противоречия можно использовать методы вычислительной гидродинамики.

Мы, однако, будем действовать в соответствии с исторической традицией и рассмотрим реальное течение с переменной поперек потока скоростью, определим потери на трение, а затем осредним скорость, перейдя таким образом к модели одномерного движения.

Будем рассматривать равномерное прямолинейное движение несжимаемой жидкости в круглой трубе (этот частный случай легко обобщается на стационарное течение в каналах переменной площади сечения).

Полагаем, что в поперечном сечении труба круглая. Для каналов с иной формой поперечника вводят условный диаметр, так называемый гидравлический диаметр, равный отношению учетверенной площади поперечного сечения к периметру:

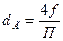, что позволяет использовать решение для круглой трубы и для некруглых труб.

Кроме того, оговоримся, что не рассматриваем сейчас течение на входном участке трубы. Согласно условию прилипания, скорость частиц жидкости на стенке равна нулю. Когда поток входит в трубу, пристенные частицы «прилипают» к твердой поверхности и начинают подтормаживать соседние, находящиеся дальше от стенки и ближе к оси трубы. Постепенно влияние стенок распространяется на всю зону течения от стенки до оси трубы. Участок течения, где вблизи оси еще остались частицы, не затронутые влиянием стенок, называется начальным. Затем устанавливается так называемое стабилизированное течение.

Опустим начальный участок, будем рассматривать только стабилизированное течение.

Изобразим профиль скорости поперек трубы (рис.5-1). 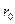- радиус трубы, 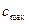- максимальная скорость (на оси трубы). Необходимо определить математически вид профиля скорости. Используем для этого второй закон Ньютона, записав, что сумма сил, действующих на выделенный элементарный объем жидкости, равна нулю (движение равномерное и прямолинейное).

Выделим в цилиндрической системе координат (ЦВС) элементарный объем в виде колечка (рис.5-2), шириной 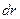и длиной 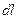. В продольном направлении действуют силы давления, равные произведению давления на площадь: 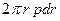на левом, входном сечении, 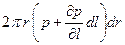на правом, выходном.

Силам давления противостоят силы трения: 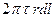на внутренней поверхности кольца (тянет жидкий объем вперед), 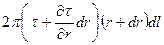на внешней поверхности кольца (тянет назад); 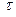- напряжение трения.

Записываем баланс сил:

.

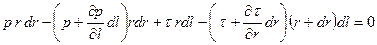Раскрываем скобки, сокращаем одинаковые слагаемые, опускаем члены порядка малости :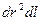

.

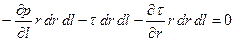Сокращаем 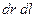и делим на :

.

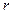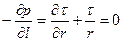Легко убедиться, что правая часть может быть преобразована к виду:

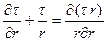, тогда

(*)

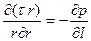Мы получили уравнение движения для стабилизированного одномерного течения несжимаемой жидкости в трубе постоянного сечения.

Заметим, что в уравнении (*) две независимых переменные 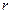и 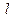, и при этом давление зависит только от продольной координаты, а напряжение трения - только от радиуса: 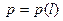, 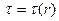(подробнее вопрос об изменении давления в поперечно направлении будет обсуждаться в теории пограничного слоя).

Таким образом, в (*) левая часть уравнения – некая функция радиуса, правая часть – функция длины, при этом при любом изменении продольной координаты и радиуса эти функции равны. Следовательно, левая и правая части уравнения – одна и та же константа. Решаем каждую часть уравнения (*) по отдельности, заменяя частные производные на полные. Постоянную, физический смысл которой пока не определен, обозначим :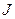

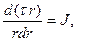(1)

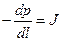. (2)

Решаем сначала уравнение (2):

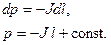
Будем отсчитывать длину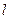от входа (начала) трубы и назначим на входе давление 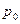. Тогда 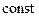равна начальному давлению: .

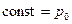Решение записывается в виде:

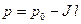(3)

Вследствие трения давление по длине трубы падает по линейному закону (рис.5-3).

Если бы изображенная на рис.5-3 прямая была наклонной плоскостью, тангент угла ее наклона 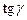назывался бы «уклон». По аналогии константа 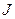называется гидравлическим уклоном.

Теперь решаем уравнение (1):

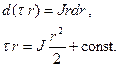
Константу определим из физических соображений. На оси трубы 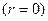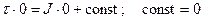кроме случая, когда напряжение трения бесконечно велико (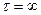), тогда получается неопределенность 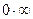, произведение может оказаться конечной величиной).

Но мы рассматриваем непрерывные среды, а бесконечное напряжение трения «порвало» бы тело. Таким образом, .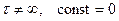

Делим на радиус правую и левую часть, получаем решение уравнения (1) в форме

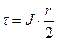(4)

Напряжение трения также распределяется по линейному закону, на оси трубы 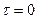(рис.5-4).

В объемном варианте, для круглой трубы, эпюра напряжения представляет собой конусообразную воронку.

Мы нашли распределение давления по длине трубы и напряжения трения по радиусу, но нас интересует распределение скорости по радиальной координате, для этого необходимо связать скорость с напряжением.

И. Ньютон предположил (это недоказуемое утверждение), что для многих жидкостей касательное напряжение пропорционально поперечной производной скорости:

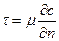
Это соотношение носит название закона трения Ньютона.

Коэффициент пропорциональности 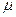называется коэффициентом динамической вязкости или просто динамической вязкостью. Определяют этот коэффициент опытным путем.

Размерность динамической вязкости: .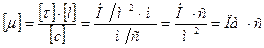

Дадим теперь определение ньютоновской жидкости.

Жидкость называется ньютоновской, если 1) на стенках ее скорость равна нулю (выполняется условие прилипания), 2) она подчиняется закону трения Ньютона.

Если хотя бы одно условие не выполнено, имеем дело с не - ньютоновской жидкостью (это очень густые, тягучие среды, такие как нефть, смолы, мазут, а также разреженные газы). Ими занимается наука реология.

Мы в дальнейшем будем считать, что наша жидкость – ньютоновская.

Возвращаемся к закону трения Ньютона. В трубе, поскольку нормаль обычно направлена от стенки в жидкость, а радиальная координата – от оси к стенке, и скорость зависит только от радиуса, нужно записать:

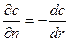
Тогда закон трения для нашей задачи:

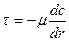(5)

Подставляем выражение для касательного напряжения трения из (5) и (4):

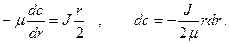
Прежде чем проинтегрировать последнее равенство, зададимся вопросом: является ли 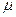постоянной ли переменной величиной? Вообще говоря, динамическая вязкость довольно существенно зависит от температуры и практически не зависит от давления: 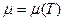. Но при отсутствии теплообмена причиной изменения температуры может быть только трение, что пренебрежимо мало, поэтому адиабатное течение несжимаемой жидкости можно считать изотермическим 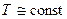(Как правило, оговорка, что рассматривается изотермическое течение, и означает, что коэффициент динамической вязкости принимается постоянным).

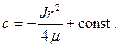
На стенке согласно условию прилипания скорость равна нулю: ,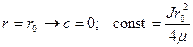

.

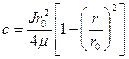Профиль скорости – парабола, ось которой совпадает с осью трубы. Для круглой трубы эпюра скорости – параболоид вращения. Дробь перед квадратной скобкой - величина скорости там, где [ ]=0, то есть скорость на оси, максимальная скорость:

.

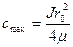Часто решение записывают так:

.

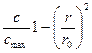Итак, давление поперек трубы постоянно, а скорость меняется по квадратичному закону. Теперь, для перехода к модели одномерного движения необходимо осреднить скорость.

Проблема осреднения никогда не имеет единственного решения, по крайней мере для трехмерных течений.

Можно определить среднюю скорость, поделив объемный расход на площадь поперечного сечения. Можно проинтегрировать по сечению количество движения и поделить на расход. Можно подсчитать удельную кинетическую энергию по сечению (она будет иметь размерность куба скорости, квадрат – собственно от кинетической энергии, первая степень скорости – от массового расхода) и извлечь из полученной величины кубический корень и т.д.

Не вдаваясь в рассуждения, какой способ осреднения «правильнее» (для разных случаев по – разному), введем среднюю скорость как осредненную по площади (иногда говорят: по расходу) и запишем:

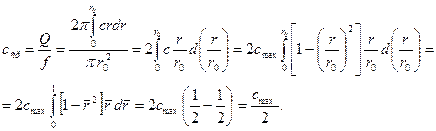
Дата добавления: 2014-01-14