Уравнение количества движения

Это уравнение связывает силу, воздействующую на тело, массу, скорость.

Для твёрдого тела это уравнение звучит следующим образом. Тело массой m_T, испытывая воздействующую на неё силу R, равную равнодействующей всех сил, приложенных к m_T, в некоторый момент времени t движется с мгновенной скоростью c_t, т.е. имеет при этом импульс m_T c _t. В момент времени t+dt его скорость станет c _t+dt, а импульс m_Т c _t+dt. Импульс силы равен приращению импульса тела R dt = m_Т c _t+dt - m_T c _t.

Рассмотрим поток рабочего тела. Введём в рассмотрение некоторый объём рабочего тела, включающий обтекаемые тела (лопатки). F – контрольная поверхность, охватывающая контрольный объём рабочего тела в момент времени t; f – площадь боковых поверхностей обтекаемых тел.

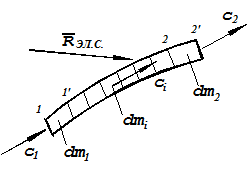
Рис.2.19. Рис.2.20.

Через период времени dt контрольный объём займет другое положение, и его поверхность станет равной F’.

Примем следующие допущения.

1. Рассматриваем стационарный поток.

2. Боковые поверхности контролируемого объёма в моменты времени t и t+dt (соответственно F и F’) практически совпадают.

Разобьём весь контролируемый объём на z элементарных струй. Рассмотрим одну их них, выбранную произвольно. Положение струи 1-2 соответствует моменту времени t. Новое положение струи 1’–2’ соответствует моменту времени t+dt.

Имеем: с ₁ – скорость на входе, с ₂ – скорость на выходе; dm₁ – масса участка 1-1’, dm₂ – масса участка 2-2’. Поскольку поток стационарный, то dm₁ = dm₂ = dm.

Разобьём участок элементарной струйки 1’-2 на n элементов. Масса каждого элемента – dm_i, скорость - с _i.

На струйку действует множество сил (давление, трение) со всех сторон. R _ЭЛ.СТР. – равнодействующая всех сил, действующих на элементарную струйку. Запишем уравнение количества движения для элементарной струйки:

Поскольку поток стационарный, с_i не изменяются с течением времени. Поэтому

.

Разделим это уравнение почленно на dt, получим уравнение количества движения для элементарной струйки: ,

где - массовый расход через элементарную струйку.

Запишем аналогичные уравнения для всех z элементарных струек контрольного объёма и сложим:

При сложении сил R _{ЭЛ.СТР.i} силы, действующие по боковым поверхностям струек взаимно компенсируются по третьему закону Ньютона. Не скомпенсированными останутся силы, действующие на поток со стороны поверхностей F и f.

(10)

Таким образом мы получили уравнение количества движения для стационарного потока: сумма сил, действующих на поток со стороны контрольной поверхности и обтекаемых тел, равна разности секундных количеств движения вытекающего и втекающего рабочего тела.

§ 2.7. УРАВНЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ

Из теоретической механики известно, что равнодействующая всех сил R, действующих на тело массой m_T и скоростью с_T, отстоящее от оси вращения на расстоянии r, создаёт крутящий момент относительно оси О-О.

Рис. 2.21.

В лопаточных машинах для скорости некоторой частицы потока с рассматривают обычно осевую, радиальную и окружную составляющие: с_a, с_r, с_u. Момент создаёт только окружная составляющая с_u.

Крутящий момент – это изменение момента количества движения, отнесённое ко времени, за которое произошло это изменение.

Рассмотрим поток рабочего тела. Ограничим рассмотрение контрольным объёмом, который охватывает контрольная поверхность. В некоторый зафиксированный момент времени t контрольная поверхность равна F, в момент времени t+dt – F’.

Рис.2.22. Рис.2.23.

Разобьём весь контрольный объём на z элементарных струек. Рассмотрим одну струйку. Считаем поток стационарным. Положение 1-2 соответствует моменту времени t, 1’-2’ – моменту времени t+dt. Скорости на входе и выходе 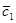и имеют окружные составляющие и 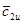. Осевые и радиальные составляющие присутствуют, но они не влияют на момент.

Равнодействующая всех сил относительно оси О-О создаёт крутящий момент Проследим перемещение элементарной струйки за время dt. Поскольку поток стационарный, то dm₁ = dm₂ = dm. Течение между сечениями 1’ и 2 разбиваем на n частей. Произвольная частица из этих n частиц имеет массу dm_i, 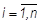, скорость 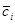, окружную составляющую скорости 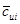и располагается на радиусе r_i. Запишем уравнение крутящего момента для элементарной струйки:

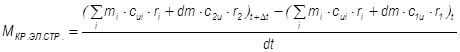
Поскольку поток стационарен, то с_i не меняется во времени, поэтому

Учтём, что 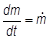- массовый расход рабочего тела через элементарную струйку.

Таким образом, получено уравнение момента количества движения для элементарной струйки.

Для всего потока (т.е. для всех z элементарных струек):

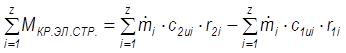
На поток действуют силы со стороны поверхностей F и f, они и создают крутящие моменты:

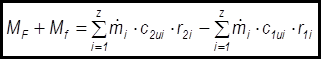(11)

Это уравнение моментов количества движения в интегральной форме для стационарного потока: сумма крутящий моментов относительно оси О-О от сил, действующих на поток со стороны контрольной поверхности F и поверхностей обтекаемых тел f, равна разности секундных моментов количества движения вытекающего и втекающего рабочего тела.

Дата добавления: 2014-01-14