Й учебный вопрос. Корреляционная и функциональная зависимости. Назначение корреляционного анализа. Понятие корреляционного поля

Между переменными (явлениями, показателями и т.п.) существуют два типа связей. Типы связей между статистическими признаками

На практике мы чаще всего сталкиваемся именно с статистическими связями (пример: зависимость между эффективностью труда сотрудников и заработной платой на различных предприятиях различно, но в целом имеет схожую тенденцию).

Существует функциональная зависимость, которая характеризуется тем, что одному значению x соответствует одно значение y. Корреляционная зависимость характеризуется тем, что одному значению x могут соответствовать несколько значений y.

Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Впервые в научном обороте термин «корреляция» был употреблён в XVIIв французским палеонтологом Жоржом Кювье в контексте корреляции частей и органов живых существ. В статистике этот термин первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века. Статистическую взаимосвязь между двумя переменными можно выявить простейшим способом — визуально. Для этого используется диаграмма рассеяния. По обеим осям откладываются соответственно значения переменных; координаты — пары.

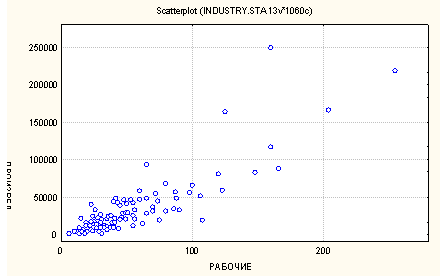
Прямая связь: большее значение одного признака ведёт к увеличению другого; обратная: увеличение одного из признаков ведёт к уменьшению другого.

Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «большее количество пожарных приводит к большему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.

Пусть существуют две переменные X и Y. X является независимой, а Y – зависимой переменной. Имеется N пар значений (X_n;Y_n), nﺂ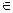N, поставленных в соответствие друг другу.

В общем случае возможно наличие двух зависимостей между X и Y. Первая из них является функциональной, вторая – корреляционной.

Функциональная зависимость y = f(x) характеризуется тем, что любому произвольно взятому значению независимой переменной Х соответствует одно вполне определенное значение зависимой переменной Y. Корреляционная зависимость y = f^*(x) характеризуется тем, что любому произвольно взятому значению независимой переменной X может соответствовать несколько значений зависимой переменной Y. Это обусловлено тем, что на Y помимо X влияют другие факторы, изменяющиеся случайным образом? в процессе наблюдения за значениями независимой и зависимой переменной X и Y.

Корреляционный, дисперсионный и регрессионный анализ используются тогда, когда мы имеем дело с корреляционной зависимостью, связывающей между собой независимую переменную X и зависимую переменную Y.

Корреляционный и дисперсионный анализ используется для оценки степени взаимосвязи:

- между двумя факторами (парный анализ);

- между некоторой совокупностью факторов и одним результирующим показателем (множественный анализ).

Используя корреляционный анализ, предполагается наличие линейности взаимосвязей, используя дисперсионный анализ такое предположение не высказывается. С этой точки зрения можно считать, что корреляционный анализ является более частным методом, чем дисперсионный анализ при решении указанной выше задачи.

Если обратиться к любому из указанных методов анализа, то необходимо отметить, что мы имеем дело с корреляционным полем. Оно включает в себя некоторую совокупность значений рассматриваемых факторов и результирующего показателя, поставленных в соответствии друг другу. В частном случае корреляционное поле включает в себя некоторую совокупность значений двух факторов, один из которых является результирующим показателем, поставленных в соответствие друг другу.

Дата добавления: 2014-01-14