Й учебный вопрос. Коэффициент линейной парной корреляции. Коэффициент линейной множественной корреляции

В парном корреляционном анализе используется значение коэффициента линейной парной корреляции r_xy, определяемое с помощью соотношения (63)

(63)

где

(64)

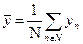
(65)

(66)

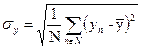
(67)

Преобразуя соотношение (63), может быть получено выражение (68)

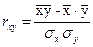
(68)

где

(69)

Получаемое значение коэффициента линейной парной корреляции может быть различным. На практике часто используется такой подход. Если значение r_xy меньше 0,3 и больше -0,3, то считается, что между x и y нет связи. Если значение r_xy попадает в интервал от 1 до 0,7, то считается, что между x и y существует тесная связь. В первом случае она прямая, во втором случае – обратная. Если значение r_xy попадает в интервалы от -0,7 до -0,3 и в интервал от 0,3 до 0,7, то считается, что нельзя с полной уверенностью говорить о наличии или отсутствии связи между x и y. В этом случае необходимо увеличить число наблюдаемых значений X_n;Y_n и повторно решать данную задачу. Если значение r_xy оказывается больше 1 и меньше -1, то считается, что между x и y существует нелинейная связь. В этом случае для оценки связи между x и y следует использовать дисперсионный анализ.

Помимо указанного выше подхода к оценке тесноты взаимосвязи между переменными x и y, может использоваться и другой подход. Он связан с оценкой значимости коэффициента r_xy с использованием расчетного и табличного значения t – статистики (закона распределения Стьюдента). Этот вопрос будет рассмотрен далее в самостоятельном разделе.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 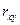для линейной регрессии 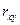(-1 ≤ ≤ 1):

,

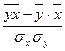где - среднее квадратическое отклонение в ряду x,

- среднее квадратическое отклонение в ряду y.

Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков связан не только с коэффициентом регрессии b, но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах.

Коэффициент эластичности отражает, на сколько процентов изменится значение y при изменение значения фактора на 1%. Коэффициент эластичности рассчитывается как .

Обобщающий (средний) коэффициент эластичности рассчитывается для среднего значения :

и показывает, на сколько процентов изменится y относительно своего среднего уровня при росте x на 1% относительно своего среднего уровня.

Точечный коэффициент эластичности рассчитывается для конкретного значения x=x₀:

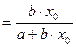
и показывает, на сколько процентов изменится y относительно своего уровня y(x₀) при увеличении на 1% от уровня x₀.

Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации. Коэффициент детерминации – это квадрат линейного коэффициента парной корреляции; он характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

,

где - сумма квадратов отклонений, обусловленная регрессией

(факторная);

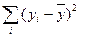- общая сумма квадратов отклонений.

Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака. Иначе, чем ближе коэффициент детерминации к 1, тем в большей степени уравнение регрессии пригодно для прогнозирования.

После того как уравнение линейной регрессии найдено, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверка значимости уравнения регрессии осуществляется путем расчета F -критерия Фишера. F -тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Непосредственному расчету F -критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений на две части: объясненную (факторную) и остаточную: ,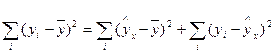

где 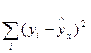- остаточная сумма квадратов отклонений.

Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должны показать, сколько независимых отклонений из n возможных требуется для образования данной суммы квадратов. Так, для общей суммы квадратов необходимо (n-1) независимых отклонений, ибо по совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) число отклонений. Например, имеем ряд значений у: 1, 2, 3, 4, 5.

, и тогда n отклонений от среднего составят: -2; -1; 0; 1; 2. Поскольку сумма отклонений равна нулю (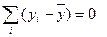), то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если четыре предыдущие известны.

При расчете объясненной, или факторной, суммы квадратов используются теоретические (расчетные) значения результативного признака, найденные по линии регрессии. При заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. df_общ = n – 1.

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы:

; ; .

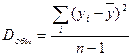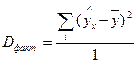Определение дисперсии на одну степень свободы приводит дисперсии к сравниваемому виду. Сопоставляя факторную и остаточную дисперсии на одну степень свободы, получим величину F- отношения, т.е. критерий F:

.

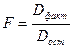При линейной связи возможно использование формул:

или ,

где m – число параметров в уравнении регрессии;

(m-1) – число степеней свободы для факторной дисперсии;

n – число наблюдений;

(n-m) – число степеней свободы для остаточной дисперсии.

Вместо числа параметров уравнения регрессии m можно использовать число коэффициентов регрессии k, которое на единицу меньше m, т.е. k=(m−1).

Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного значения F-критерия. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:

F_табл‹ F_факт, гипотеза Н₀ отклоняется.

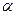F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы () и уровне значимости , который принимается равным 0,05 или 0,01.

Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без риска сделать неправильный вывод о наличии связи.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартной ошибки:

; .

Стандартные ошибки параметров линейной регрессии и коэффициент корреляции определяются по формулам:

,

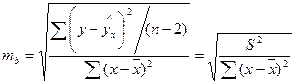где S² – остаточная дисперсия на одну степень свободы;

;

Сравнивая фактическое t_факт и критическое (табличное) значения t -статистики t_табл (при определенном уровне значимости 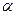и числе степеней свободы (n-2)) – принимаем или отвергаем гипотезу Н₀. Если t_табл < t_факт,то Н₀ отклоняется, т.е. a, b, r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт,то гипотеза Н₀ не отклоняется и признается случайная природа формирования a, b, r_xy.

Рассмотренную формулу оценки коэффициента корреляции рекомендуется применять при большом числе наблюдений, а также если r_xy не близко к +1 или –1. Если же величина r_xy близка к +1, то распределение его оценок отличается от нормального, или распределения Стьюдента, так как величина коэффициента корреляции ограничена значения от –1 до +1. Для устранения данного затруднения Р.Фишер ввел вспомогательную величину z, связанную с r_xy следующим соотношением: . При изменении r_xy от –1 до +1 величина z изменятся от 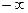до 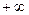, что соответствует нормальному распределению.

Стандартная ошибка величины z рассчитывается по формуле:

.

Для расчета доверительного интервала определяем предельную ошибку для каждого показателя:

Формулы для расчета доверительных интервалов имеют следующий вид:

; ; ;

; ; .

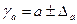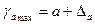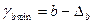Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение y_p определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x_p. Вычисляется стандартная ошибка прогноза :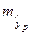

.

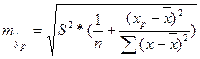Величина стандартной ошибки достигает минимума при x_p =и возрастает по мере того, как «удаляется» от в любом направлении. Можно ожидать наилучшие результаты прогноза, если признак-фактор находится в центре области наблюдений х.

Доверительный интервал прогноза:

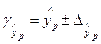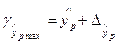; ; , где .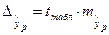

Однако так как фактические значений у варьируют около среднего значения 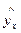, индивидуальные значения у могут отклоняться от 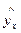на величину случайно ошибки , дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S². Поэтому ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку, но и случайную ошибку. Средняя ошибка прогнозируемого индивидуального значения составит:

.

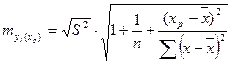Для определения значения коэффициента линейной множественной корреляции 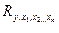, где y – результирующий показатель, а x₁, x₂ … x_n – факторы, используется формула (70)

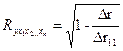
(70)

где - определитель матрицы парных коэффициентов корреляции; - определитель матрицы межфакторной корреляции.

Определитель имеет вид (71)

(71)

Матрица получается тогда, когда из матрицы вычеркивается 1 столбец и 1 строка. В результате определяется выражением (72)

(72)

Чем ближе значение коэффициента линейной множественной корреляции к 1, тем теснее считается связь между результирующим показателем Y и совокупностью факторов x₁, x₂ … x_n

Корреляционный анализ является одним из методов статистического анализа взаимосвязи нескольких признаков. Он применяется тогда, когда данные можно считать случайными и выбранными из генеральной совокупности распределенной по многомерному, нормальному закону.

Основная задача корреляционного анализа состоит в оценке корреляционной матрицы и определении на ее основе частных и множественных коэффициентов корреляции и детерминации.

Парный коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными на фоне действия всех остальных показателей входящих в модель.

Частный коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными при исключении влияния всех остальных показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем, чем ближе коэффициент корреляции к ±1,тем сильнее зависимость между переменными. Если коэффициент корреляции больше нуля, то связь положительная, если меньше, то отрицательная.

Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель; изменяется в пределах от 0 до 1.

Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации и он характеризует долю дисперсии одной переменной (результативной),обусловленной влиянием всех остальных (аргументов),входящих в модель.

Исходной для анализа является матрица:

Размерность n´k i –строка, которой характеризует i –наблюдение (объект) по всем k-показателям, где i –число наблюдений. i=1...n, j=1...k

В корреляционном анализе матрицу Х рассматривают, как выборку объема n из k-мерной генеральной совокупности подчиняющейся k-мерному нормальному распределению.

При выборке определяют оценки параметров генеральной совокупности, а именно: вектор средних (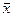),вектор средне – квадратичных отклонений (S) и корреляционную матрицу (R) порядка к.

В корреляционном анализе матрицу Х рассматривают, как выборку объема n из k-мерной генеральной совокупности подчиняющейся k-мерному нормальному распределению.

При выборке определяют оценки параметров генеральной совокупности, а именно: вектор средних (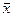),вектор средне – квадратичных отклонений (S) и корреляционную матрицу (R) порядка к.

S= R=

Матрица R является симметричной (r_jl = r_lj) и положительно распределенной, где

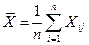
_n

S_j = 1/n∑ (x_ij - 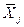)²

ⁱ⁼¹

r_jl = ,

где x_ij – значение i-го наблюдения j-го фактора.

R_jl – выборочный парный коэффициент корреляции, характеризующий тесноту линейной связи между показателями х_j и х_l.При этом X_jl является оценкой генерального парного коэффициента корреляции. Кроме того, находятся точечные оценки частный и множественных коэффициентов корреляции любого порядка. Например, частный коэффициент корреляции (к-2) порядками между факторами х₁ и х₂ равен r_12/34...k = ,

где R_jl - алгебраическое дополнение элемента r_jl к корреляционной матрице R,при этом

R_jl = (-1)^i+l * M_jl,

где M_jl – минор, определитель матрицы, получаемый из матрицы R путем вычеркивания j-строки и l-столбца.

Множественный коэффициент корреляции (к-1) порядка фактора (результативного признака х₁) определяется по формуле,

r_1/2…k=r₁=,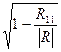

где 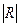-определитель матрицы R.

При определении с надежностью γ доверительного интервала для значимого, парного или частного коэффициента r, используют z-преобразования Фишера и предварительно установленную оценку для z:

Z′ - 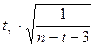≤ Z′ +

где t_γ вычислено ар таблице интегральной функции Лапласа из условия, что Ф(t_γ)= γ

Значение Z′ определяется по таблице z-преобразований по найденному значению r.Функция нечетная, т. е Z′(- r)= - Z′(r)

Обратный переход от z к ρ осуществляется так же по таблице z-преобразований после использования, которой получим интервальную оценку для ρ с надежностью γ.

r_min≤ ρ ≤r_max

Дата добавления: 2014-01-14