Определенный интеграл и его свойства

Лекция 6

6.1. Задача, приводящая к понятия определенного интеграла

Пусть на интервале [a,b] задана непрерывная функция y=f(x) такая, что f(x)³0. Поставим следующую задачу: найти площадь, ограниченную снизу осью Ox, с боков прямыми x=a и x=b и сверху графиком функции y=f(x). Эту фигуру назовем криволинейной трапецией. Разобьем интервал на части системой точек a=x₀, x₁, x₂,...,x_n-1,x_n=b. Для определенности считаем a<b. Интервал [a,b] разобьется на достаточно малые части. Обозначим Dx_i=x_i- x_i-1. Выберем на каждом интервале x=x_iÎ[ x_i-1,x_i], i=1,2,...,n. Вычислим в каждой из точек значение y_i=f(x_i) и найдем произведение f(x_i)Dx_i. Просуммируем полученные произведения.

(1)

y

y=f(x)

O a=x₀ x₁x₂ x_i x_i x_n=b x

Рис. 1. Построение интегральной суммы

Из геометрического смысла картины ясно, что произведение f(x_i)Dx_i - это площадь прямоугольника с высотой f(x_i) и шириной Dx_i, а сумма (1) - это площадь ступенчатой фигурки, изображенной на рис. 1. Ясно, что сумма (1) приближенно равна площади криволинейной трапеции.

6.2. Определение и существование определенного интеграла

Пусть дана произвольная функция y=f(x) и произвольный интервал [a,b] (причем необязательно, чтобы a<b и f(x)³0). Разобьем интервал [a,b] на достаточно большое число достаточно малых частей системой точек a=x₀, x₁, x₂,...,x_n-1,x_n=b и построим сумму (1). Сумма (1) называется интегральной суммой. Обозначим maxçDx_iç=l. Начнем строить различные интегральные суммы так, чтобы l®0 и, соответственно, n®¥.

Определение. Предел интегральных сумм вида (1) при l®0, если этот предел существует и не зависит ни от способа разбиения интервала [a,b] на части, ни от выбора значений x=x_i на интервалах[ x_i-1,x_i], называется определенным интегралом на интервале [a,b] от функции y=f(x) по dx. Обозначается

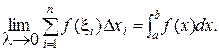(2)

Геометрический смысл определенного интеграла

Из рассмотренного геометрического построения ясно, что, если f(x)³0 и a<b, то интеграл (2) равен площади указанной криволинейной трапеции.

Определение. Функция y=f(x) заданная на интервале [a,b], называется кусочно-непрерывной, если интервал [a,b] можно разбить на конечное число частей, на каждом из которых она непрерывна, а на концах этих интервалов имеет разрывы первого рода.

Теорема. Если функция y=f(x) кусочно-непрерывнa на интервале [a,b], то интеграл (2) существует. (Без доказательства).

6.3. Свойства определенного интеграла

Пусть указанные интегралы существуют. Тогда выполняются следующие свойства.

1. Постоянный сомножитель можно выносить за знак определенного интеграла.

2. Определенный интеграл от алгебраической суммы слагаемых равен алгебраической сумме определенных интегралов от слагаемых.

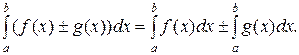
3. Если на интервале [a,b] выполнено неравенство

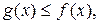
то

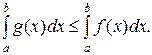
4. Если на интервале [a,b] выполнено неравенство

где m - наименьшее значение, M - наибольшее значение функции y=f(x) на интервале [a,b], то

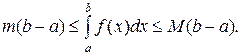
5. Если функция y=f(x) на интервале [a,b] непрерывна, то существует точка xÎ [a,b] такая, что

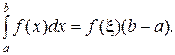
6. При перестановке пределов интегрирования перед интегралом появляется знак минус.

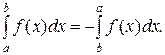
7. Каковы бы ни были величины a,b,c выполнено свойство

8. Определенный интеграл не зависит от переменной интегрирования

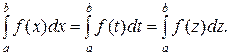
Разобрать доказательство этих свойств самостоятельно по учебнику. Приведем доказательство свойства 5. Так как функция y=f(x) на интервале [a,b] непрерывна, то существует m - наименьшее значение, M - наибольшее значение функции y=f(x) на интервале. Из свойства 4 следует

Непрерывная функция принимает на интервале [a,b] все промежуточные значения от m до M. Тогда существует такая точка xÎ [a,b], что

Откуда и следует утверждение теоремы.

6.4. Определенный интеграл с переменным верхним пределом

Рассмотрим случай, когда задан определенный интеграл от функции y=f(x), которая определена на интервале [a,b], и верхний предел является переменной величиной xÎ[a,b]. В этом случае определена некоторая функция F(x)

(3)

Теорема. Если функции y=f(x) определена и непрерывна на интервале [a,b], то

(4)

Доказательство.

y

y=f(x)

O a x x x+Dx

Рис. 1.Геометрическое изображение интеграла с переменным верхним пределом

Найдем приращение функции

где xÎ[x,x+Dx]. По определению производная равна

Теорема доказана.

Дата добавления: 2014-01-14