Несобственный двойной интеграл по неограниченной области

Пусть – неограниченная область в плоскости XOY, ее граница проходит через бесконечно удаленную точку (например, полуплоскость или внутренняя часть области, ограниченной двумя лучами с общей вершиной. Пусть функция определена и непрерывна в любой внутренней точке области . Что мы будем понимать под 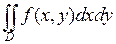? Естественно, что введенное выше определение двойного интеграла здесь невозможно, так как невозможно разбить неограниченную область на конечное число ограниченных квадрируемых подобластей, да еще и менять разбиения так, чтобы диаметры подобластей стремились к нулю.

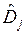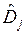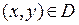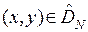Назовем исчерпанием области последовательность подобластей , , таких, что , каждая область ограничена и квадрируема, и для любой точки найдется номер такой, что . Таким образом, с увеличением номера 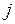подобласти 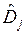, расширяясь, все более приближаются к области . В качестве примера можно рассмотреть в качестве области верхнюю полуплоскость, а в качестве последовательности подобластей 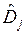– последовательность лежащих в верхней полуплоскости полукругов, опирающихся на отрезки как на диаметры.

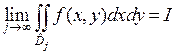Построив исчерпание, рассмотрим последовательность . Если существует , причем при любом другом исчерпании области предел будет таким же, то назовем 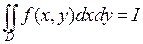несобственным двойным интегралом по неограниченной области.

П р и м е р. Исследовать сходимость , где 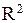– вся плоскость XOY. Будем исчерпывать плоскость кругами , где n – натуральное число. Для вычисления двойного интеграла по каждому из кругов удобно перейти к полярным координатам по формулам 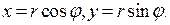Тогда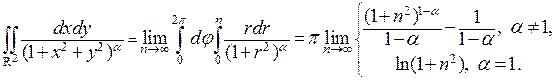

Очевидно, что при 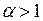предел существует, при 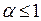предел бесконечен. Можно показать, что при 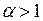предел не зависит от способа исчерпания. Поэтому рассмотренный несобственный интеграл сходится при 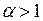и расходится при .

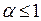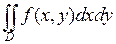Для введенных кратных несобственных интегралов от положительных функций справедливы теоремы сравнения: а) если сходится интеграл от большей функции, то сходится интеграл от меньшей функции, б) если существует конечный предел , то из сходимости следует сходимость .

П р и м е р. Доказать, что интеграл сходится.

Найдем с применением правила Лопиталя

.

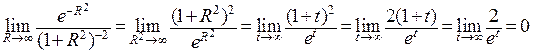В соответствии со второй теоремой сравнения из сходимости 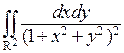следует сходимость .

Применим полученные сведения для вычисления важного интеграла 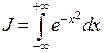. Для этого вычислим интеграл двумя способами: а) с помощью исчерпания плоскости кругами с увеличивающимися радиусами и б) с помощью исчерпания плоскости квадратами с увеличивающимися длинами сторон.

а) .

б) .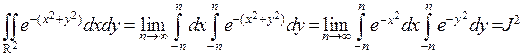

Из равенства левых частей полученных соотношений а) и б) имеем:

.

Рассмотрим еще более сложный интеграл, применяемый в курсе «Уравнения математической физики»:

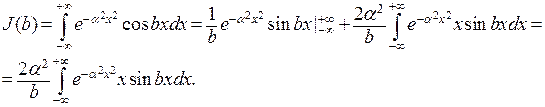
Нетрудно видеть из определения интеграла , что при дифференцировании по параметру 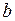получим: 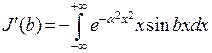. Следовательно, этот интеграл удовлетворяет уравнению 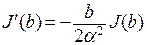. Решая это уравнение, получим . Используем начальное условие и наконец получим .

Дата добавления: 2014-01-14