Лекция 3. Статистическое изучение динамики

Если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической х, то он всегда будет больше среднего квадрата отклонений о2, исчисленного от средней арифметической.

Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится.

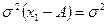(7.7)

2. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А² раз, а среднее квадратическое отклонение - в А раз:

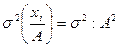(7.8)

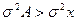(7.9)

При этом больше на вполне определенную величину - на квадрат разности между средней и этой условно взятой величиной, т.е. на (х - А)²:

или

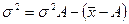(7.10)

Дисперсия от средней имеет свойство минимальности, т. е. она всегда меньше дисперсий, исчисленных от любых других величин. В этом случае, когда А приравниваем к 0 и, следовательно, не вычисляем отклонения, формула принимает такой вид:

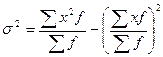или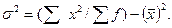

Значит, средний квадрат отклонений 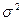равен среднему квадрату значений признака 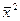минус квадрат среднего значения признака (х)², т.е..

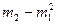Изложенный способ расчета дисперсии и среднего квадратического отклонения называется способом моментов, или способом отсчета от условного нуля. Он применим при условии равных интервалов.

Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим формулу

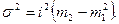(7.12)

Используем изложенные выше свойства дисперсии для расчета показателей по региону 2. Так, средняя в данном примере равна: х = А+im_]=110+20(- 0,25) = 105 млн. руб. Дисперсия 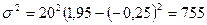и среднеквадратическое отклонение 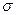=27,477 млн. руб. 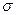выражается в именованных числах.

Средняя величина отражает тенденцию развития, т. е. действие главных причин (факторов), 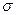измеряет силу воздействия прочих факторов.

Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении

разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

(7.13)

В регионе 2 разница между крайними значениями на 14,3% превышает среднее значение товарооборота на одно предприятие.

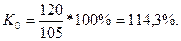
В то же время в регионе 1 этот показатель составляет 38,1% среднего значения.

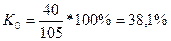
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

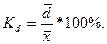(7.14)

В регионе 2 он составил 21,7% против 5,3% в регионе 1

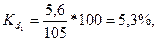
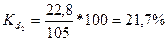
3. Коэффициент вариации

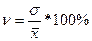(7.15)

тогда ,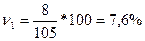

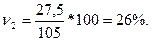
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. При этом исходят из того, что если v больше 40%, то это говорит большой колеблемости признака в изучаемой совокупности. В нашем примере коэффициент вариации подтверждает большую колеблемость товарооборота в регионе 2.

Виды дисперсий и закон (правило) сложения дисперсий. Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в своих расчетах, мы не можем определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений (вариант) признака.

Это можно сделать при помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку-фактору. При этом можно определить три показателя колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внутригрупповых дисперсий.

Дата добавления: 2014-01-11