Регион 2

Регион 1

Группы предприятий по объему товарооборота,	Число предприятий	Расчетные показатели
млн руб.
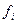
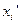
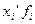
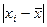
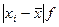
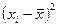
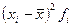
							8
90—100 28		2 660	-10	-280		2 800
100—110 48		5 040
110—120 20						2 000
120—130 4						1 600
Итого 100		10 500				6 400

Таблица 7.2

Группы	Число	Расчетные показатели
Предприятий по объему товарооборота, млн руб.,	предприятий
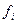
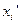
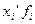
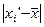
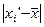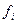
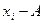
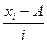
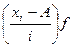
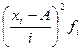
60—80		70 1470	-35	-735	-40	-2	-42
80—100		90 2430	-15	-405	-20	-1	-27
100—120		110 2640
120—140		30 2080
140—160		150 1200				о
160—180		170 680

Итого 100 10 500 22 80 -25 195

Средний объем товарооборота на одно предприятие по регионам равен 105 млн. руб.:

регион 1: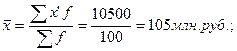

регион 2: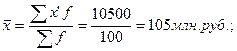

Регион 1: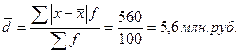

Регион 2: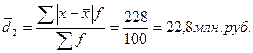

В нашем примере в регионе 1 показатели объема товарооборота более однородны, чем в регионе 2. Среднее линейное отклонение как меру вариации признака применяют в статистической практике редко. Во многих случаях этот показатель не устанавливает степень рассеивания.

На практике меру вариации более объективно отражает показатель дисперсии (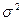- средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат (х—х)²:

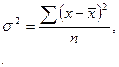(7.4)

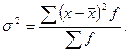(7.5)

Корень квадратный из дисперсии 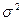среднего квадрата отклонений представляет собой среднее квадратическое отклонение

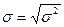(7.6)

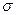и 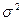являются общепринятыми мерами вариации признака. Так, по региону 1 дисперсия составила:

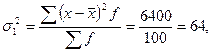
и среднеквадратическое отклонение соответственно:

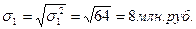
По региону 2:

и

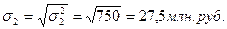
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. Как видим, в регионе 1 дисперсия и среднее квадратическое отклонение значительно меньше, чем в регионе 2, что также подтверждает большую надежность средней в регионе 1.

Дисперсия обладает рядом свойств (доказываемых в математической статистике), которые позволяют упростить расчеты.

Дата добавления: 2014-01-11