Преобразования Галилея

В связи с относительностью движения часто возникает необходимость перехода из одной инерциальной системы отсчёта в другую. В классической механике такой переход осуществляется с помощью преобразований Галилея. Эти преобразования связывают между собой координаты какой-либо материальной точки в двух различных инерциальных системах отсчёта, когда скорости движения много меньше скорости света.

Пусть относительно инерциальной системы отсчёта K движется со скоростью u другая система отсчёта K¢. Для упрощения рассуждений предположим, что направления координатных осей Ox и O¢x¢ совпадают (рис. 1). Обозначим координаты точки M в системе отсчёта K в произвольный момент времени t через x, y, z, а координаты той же точки в системе отсчёта K ¢ — через x ¢, y ¢, z ¢ в тот же момент времени t ¢. В классической механике считается, что время в любой инерциальной системе отсчёта течёт одинаково, т.е. t = t ¢. Допустим, что в момент времени t = t ¢ = 0начала координат совпадали, т.е. x = x ¢ = 0. Тогда, как видно из рис. 1, в момент времени t координаты материальной точки y = y ¢ и z = z ¢, а абсциссы отличаются на отрезок OO ¢ = ut. Отсюда преобразования Галилея при переходе от одной системы отсчёта к другой принимают вид:

x

u

ut x¢

O

O ¢

y

y¢¢

M

y= y¢

z=z¢¢

K¢

K

z z¢

x¢

x

Рис. 1

К ® К¢ К¢ ® К

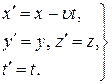(1) (2)

СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ГАЛИЛЕЯ

Из преобразований Галилея вытекает ряд следствий.

1. Классический закон сложения скоростей. Пусть точка М движется с некоторой скоростью u ¢ относительно системы К ¢. Какова скорость этой точки в системе К? Для ответа на этот вопрос продифференцируем уравнения (2) по времени: 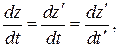так как производная по t равна производной по t¢. Эти выражения можно переписать:

(3)

где 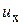, , 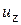¾ проекции скорости материальной точки на координатные оси в системе отсчёта K, а 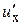, , 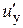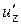¾ проекции скорости 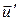той же точки на координатные оси в системе K¢. Умножая (3) на соответствующие координатные орты и складывая равенства, получаем: 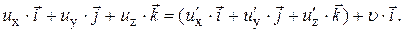Тогда получаем:

(4)

Итак, скорость тела, одновременно участвующего в двух движениях, равна векторной сумме скоростей этих движений.

2. Ускорение в различных инерциальных системах отсчета. Дифференцируя уравнение классического закона сложения скоростей (уравнение (4) из предыдущей лекции) по времени, получаем: так как поскольку 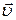= const. Отсюда

(5)

Таким образом, ускорение в разных инерциальных системах отсчёта в классической механике является неизменной величиной. Величины, которые не меняются при переходе от одной системы отсчёта к другой, называются инвариантными.

3. Длина отрезка в различных инерциальных системах отсчёта. Длиной отрезка называют разность координат его конца и начала, измеренных одновременно. Пусть стержень расположен параллельно оси абсцисс и покоится в системе отсчёта K¢, которая движется относительно системы K со скоростью u, причём оси абсцисс этих систем совпадают. Предположим, что длина стержня в системе K¢ равна: где и ¾ координаты начала и конца стержня. Найдём его длину l = x ₂ - x ₁, где x ₁ и x ₂ ¾ координаты начала и конца стержня в системе отсчёта K, относительно которой он (вместе с системой отсчёта K¢) движется со скоростью u. По определению длины отрезка с использованием преобразования Галилея (1) запишем, что так как координаты концов измеряются в один и тот же момент времени t. Итак,

l¢ = l, (6)

т.е. в различных инерциальных системах отсчёта длина отрезка одинакова.

ПОСТУЛАТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ.

Преобразования Галилея и следствия из него настолько очевидны, то кажется, что они должны быть справедливыми во всех случаях. Однако в конце 19 века был обнаружен один факт, противоречащий классическому закону сложения скоростей, следовательно, и преобразованиям Галилея ¾ это постоянство скорости света в вакууме в различных инерциальных системах отсчёта. Например, скорость света при движении Земли по её орбите навстречу Солнцу и от него получалась одинаковой и равной c» 3×10⁸ м/с, а не c ± u, где u — орбитальная скорость Земли, как это должно следовать из классического закона сложения скоростей. В связи с этим возникла необходимость в отказе от привычных представлений о пространстве и времени, используемых в классической механике, поскольку они противоречили опытному факту постоянства скорости света.

Релятивистская механика, созданная Эйнштейном, основывается на двух постулатах:

а) Принцип относительности. Все инерциальные системы отсчёта равноправны, во всех таких системах не только механические, но и все другие явления природы протекают одинаково.

б) Принцип постоянства скорости света. Во всех инерциальных системах отсчёта скорость света в вакууме одинакова и равна с.

Правильность этих постулатов и всей релятивистской механики следует из того, что следствия, получаемые из теории Эйнштейна, находят надёжное экспериментальное подтверждение. Первый постулат требует существования преобразований, аналогичных преобразованиям Галилея, которые бы оставляли неизменными уравнения механики и электродинамики при переходе от одной инерциальной системы отсчёта к другой.

Дата добавления: 2014-01-14