Преобразования Лоренца

Пусть относительно инерциальной системы отсчёта K движется со скоростью u другая система отсчёта K¢. Для упрощения рассуждений предположим, что направления координатных осей Ox и O¢x¢ совпадают (рис. 1 предыдущей лекции). Обозначим координаты точки M в системе отсчёта K в произвольный момент времени t через x, y, z, а координаты той же точки в системе отсчёта K ¢ — через x ¢, y ¢, z ¢ в момент времени t ¢. Тогда преобрaзования при переходе из системы отсчёта K¢ в систему K имеют вид:

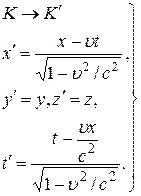(7) (8)

Соотношения (7) и (8) носят название преобразований Лоренца.

В классической механике понятия пространства и времени являются независимыми. Из преобразований же Лоренца видна тесная связь между пространством и временем, поскольку время зависит от пространственных координат. Таким образом, в релятивистской механике рассматривается не трёхмерное пространство, к которому добавляется понятие времени, а четырёхмерное пространство с неразрывно связанными временными и пространственными координатами.

НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА

Из преобразований Лоренца вытекает ряд следствий, необычных с точки зрения классической механики.

1. Предельный характер скорости света. В классической механике считается, что тела могут двигаться с любыми сколь угодно большими скоростями. Из преобразований Лоренца, однако, следует, что 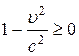(иначе 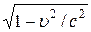¾ мнимый корень). Поэтому 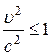и 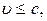т.е. скорость тела не может быть больше скорости света в вакууме.

2. Длина тел. Рассмотрим стержень, расположенный вдоль оси абсцисс и покоящийся в системе отсчёта K. Длина стержня l в этой системе отсчёта равна l = x ₂ - x ₁, где x ₁ и x ₂ ¾ координаты начала и конца стержня, не изменяющиеся со временем, так как он неподвижен. Предположим теперь, что он находится в системе отсчёта K¢, которая движется относительно системы K со скоростью u. При этом оси абсцисс систем отсчёта совпадают. Можно показать, что длина l¢ этого стержня с точки зрения наблюдателя, находящегося в системе отсчёта К, равна

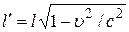, (9)

т.е. длина стержня, измеренная в системе отсчёта, относительно которой он движется, меньше длины, измеренной в системе, в которой он покоится. Необходимо отметить, что в направлении осей ординат и аппликат размеры стержня в данном случае не меняются.

Дата добавления: 2014-01-14