Интерферометрлер

Интерференция құбылысы дәлді өлшеуіш приборларда - интерферометрлерде қолданылады. Мысал ретінде Майкелсон интерферометрінің жұмыс принціпімен танысайық (2.2.6.1 -сурет).

2.2.6.1-сурет

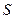жарық көзінен монохроматты жарық жартылай мөлдір жазық параллель пластинаға 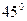бұрышпен түседі. Пластинада жарық екі сәулеге ажырайды. 1-ші сәуле 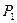пластинасынан шағылып, 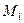айнаға келіп, одан да шағылып, кері қайтып 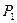пластинасы арқылы өтеді (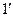). 2-ші сәуле 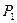пластинасынан өтіп, айнасынан шағылып келіп, қайтадан 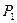пластинасынан шағылады (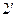). 1-ші сәуле 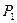пластинасынан 2 рет өткендіктен жол айырмасын теңестіру үшін 2-ші сәуленің жолына қалыңдығы 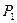пластинаның қалыңдығындай 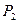пластинасы қойылады.

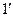-ші және 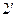-ші сәулелер когерентті: сондықтан олар интерференцияланады және нәтижесі 1-ші сәуленің 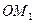, 2-ші сәуленің 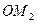оптикалық жол ұзындықтарының айырымына байланысты болады. Айналардың біреуін 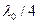қашықтыққа ығыстырса екі сәуленің жол айырмасы 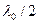өзгеретіндіктен көру өрісінің жарықталынуы ауысады. Интерференциялық жолақтың ығысуына байланысты айналардың ығысу қашықтығын анықтауға болады. Майкельсон интерферометрі ұзындықтарды дәл өлшеулер үшін қолданылады (денелердің ұзындығын, жарық толқынын ұзындығын, темрератураның өзгерісіне байланысты дененің ұзындығының өзгерісін). Интерфеометрлердің түрі көп, бірақ жұмыс істеу принциптері бірдей.

2.3 Жарық дифракциясы

Дифракция деп толқындардың жолындағы бөгеттерді орай өтуін немесе толқынның түзу сызықты таралуынан кедергінің маңында кез-келген ауытқуын айтады. Бұл құбылыс дыбыс толқындарында жақсы байқалады. Мысалы, дыбыс үй сыртында да естіледі, себебі дыбыс толқыны үй бұрышын айналып өтеді. Жарық та электромагниттік толқын, сол себепті жарық үшін дифракция құбылысы орын алады.

Дифракция құбылысы Гюйгенс принципімен түсіндіріледі. Гюйгенс принціпі бойынша 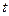мезеттегі толқын майданы белгілі болса, келесі (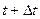) мезеттегі толқын майданын анықтауға болады. Өйткені толқын майданының әрбір нүктесі толқын көзі болып табылады. Бұл екінші реттік толқындарды ораушы жаңа толқын майданы болып табылады. Мысал ретінде бір саңылауға келіп жеткен жазық толқын майданын қарастырайық. (2.3.1-сурет).

Толқын майданы бөгетке келгенде оның әрбір нүктесі екінші толқын көзі болып шығады. Осы толқындардың ораушысы саңылаудан өткен толқынның майданы болып табылады. Гюйгенс принціпі толқындық майданның таралу бағытын анықтауға мүмкіндік береді, ал амплитудасы, оған сәйкес әр түрлі бағыттағы таралатын толқын интенсивтілігі анықталмайды. Себебі толқын амплитудасының квадраты жарық интенсивтілігін береді. Гюйгенс принципін толықтыратын Френельдің ұсынған тәсілі бұл кемістікті жояды.

2.3.1 Френель зоналары. Жарықтың түзу сызықты таралуы

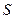жарық көзінен шыққан толқынның 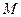нүктесіндегі амплитудасын анықтайық (2.3.1.1-сурет). Френель Ф толқын бетін сақиналық зоналарға бөлді және зоналардың 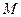нүктесінен қашықтығы 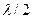шамасына өзгеріп отыратындай етіп бөлінеді.

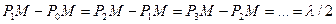
центрлеріі 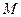нүктесінде, радиустары

сфералар жүргіземіз. Осы шарттар орнындалғанда көршілес зоналардан 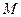нүктесіне келетін тербелістердің жүріс айырмасы 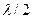тең болады, сонда 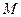нүктесіне келетін бұл тербелістер қарама-қарсы фазада болады да, бірін-бірі әлсіретеді. 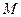нүктесіндегі қорытқы тербеліс амплитудасы

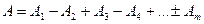(2.3.1.1)

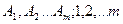зоналарының тудыратын амплитудалары.

2.3.1.1-сурет

Тербеліс амплитудаларын анықтау үшін Френель зоналарының аудандарын есептейік. 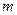-ші зонаның сфералық сегментінің биіктігі 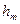(2.3.1.2 сурет).

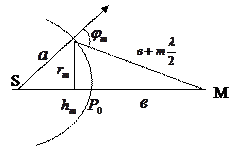
2.3.1.2 сурет

;

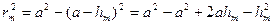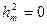
болғандықтан 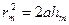(2.3.1.2)

екіншіден

; ;

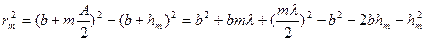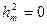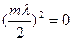
сонда

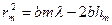(2.3.1.3)

(2.3.1.2) мен (2.3.1.3) теңестіріріп 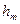-ты анықтауға болады

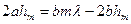
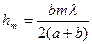(2.3.1.4)

Сфералық сегменттің ауданы

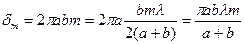
Френельдің 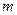-ші зонасының ауданы

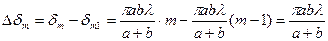(2.3.1.5)

Бұл формула 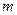-ға байланыссыз болғандықтан зоналардың аудандары бірдей болады. Зоналардың саны артқан сайын зоналардың 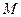нүктесінен қашықтығы арта береді. Олай болса зоналардан келетін жарықтың интенсивтілігі кеми береді және зоналардың саны 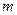артқан сайын 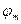бұрышы үлкейе береді де 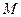нүктесіне әсері азая береді. Осы жағдайда

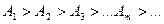
Жуықтап алғанда 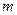-ші зонаның амплитудасы

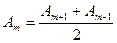
Онда (2.3.1.1) формула

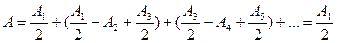(2.3.1.6)

түрде жазылады, себесі жақша ішіндегі шамалар нөлге тең, ал соңғы зонаның аммплитудасы өте аз шама 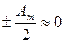. Сфералық толқынның 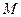нүктесіндегі амплитудасы орталық зонаның тудыратын амплитудасының жартысына тең болады.

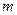-ші зонаның радиусын (2.3.1.2) -ға (2.3.1.4) –ны қойса

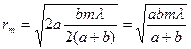(2.3.1.6)

Мысалы, 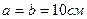, 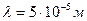болса, бірінші (орталық) зонаның радиусы 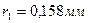болады. Яғни, жарық 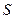нүктесінен 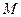нүктесінде 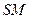түзуінің бойымен таралады деуге болады (жарықтың түзу сызықты таралуы).

Сонымен Гюйгенс-Френель принціпі біртекті ортажа жарықтың түзу сызықты таралуын да түсіндіре алады.

2.3.2 Дөңгелек тесіктегі және дискідегі Френель дифракциясы

Дифрациялық бейне дифракция тудырушы бөгеттен өте үлкен қашықтықта пайда болса оны Френель дифракциясы немесе сфералық толқындардың дифракциясы дейді.

1. Дөңгелек тесіктегі дифракция.

S нүктелік жарық көзінен шыққан сфералық толқын жолына дөңгелек саңылауы бар қалқан қойылсын да, Э экранның В нүктесіндегі дифракциялық бейнені байқылансын (2.3.2.1-сурет). Экран тесік жазықтығына параллель және одан 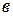қашықтыққа орналасқан. Дифракциялық бейненің көрінісі тесікке сиятын Френель зоналарының санына байланысты. В нүктесіндегі қорытқы тербеліс амплитудасы

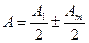
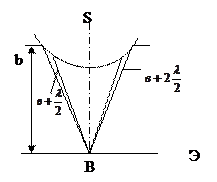
2.3.2.1-сурет

мұнда (+) зона саны тақ болғанда, ал (-) зона саны жұп жағдайға сәйкес. Егер саңылау тақ зона санын ашса, онда В нүктесіндегі амплитуда (қарқындылығы) толқын еркін таралғандығынан үлкен болады, ал зона саны жұп болса, онда амплитуда нөлге тең болады. Егер саңылауға Френельдің бір зонасы сыйса, онда В нүктесіндегі амплитуда 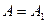болады, ал екі зона сыйса, онда В нүктесіндегі әсері бірін-бірі жояды.

Сонымен, дөңгелек тесіктің дифракциялық бейнесі центрі В нүктесінде орналасқан қараңғы және жарық сақиналар болып табылады. Егер 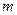жұп болса центрде қараңғы сақина, ал 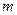тақ болса жарық сақина болады. Осы кезектесіп отыратын қараңғы және жарық сақиналардың интенсивтілігі центрден қашықтаған сайын азая береді. Егер саңылауға монохроматты емес, ақ сәуле түссе сақиналар боялған болады.

2. Дискідегі дифракция

Нүктелік 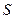жарық көзінен шыққан сфералық толқын жолына диск орналастырылсын (2.3.2.2-сурет). Дифракциялық бейне 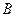нүктесінде байқалады. Толқынның диск жапқан бөлігін алып тастап, қалған зоналарын Френель зоналарына бөлеміз. Бөліну диск шетінен басталады. Диск алғашқы 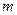Френель зоналарын жапсын дейік. Онда В нүктесіне қалған зоналардан тербелістер келеді. В нүктесіндегі қорытқы тербеліс амплитудасы

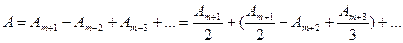
немесе жақша ішіндегі шама н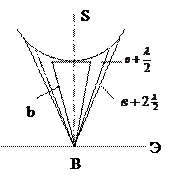өлге тең болғандықтан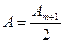

2.3.2.2-сурет

Ендеше В нүктесінде әр уақытта интерференциялық максимум (жарық дақ) байқалады. Осы орталық жарық дақты концентрлі қараңғы және жарық сақиналар қоршай орналасады.

2.3.3 Бір саңылаудағы Фраунгофер дифракциясы

Жазық жарық толқындардың немесе параллель сәулелердің дифракциясын Фраунгофер дифракциясы дейді. Бұл жарық көзі мен бақылау нүктесі дифракцияция тудырушы бөгеттен шексіз алыс орналасқан жағдайда орын алады. Ол үшін нүктелік көзді жинағыш линзаның фокусына орналастыру қажет те, дифракциялық бейнені бөгеттің арғы орналастырылған екінші жинағыш линзаның фокальдық жазықтығында қарастыру керек.

Фраунгофер линзаның фокалдық жазықтығындағы дифракциялық бейнені бақылады. 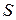нүктелік жарық көзі 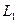линзаның фокалдық жазықтығында орналасса, сәулелер шоғы линзадан параллель шығады.(2.3.3.1 -сурет). Осы сәулелер кеңдігі 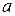саңылауға түседі. Шеткі 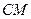және 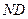сәулелерінің оптикалық жүріс айырмасы:

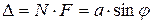(2.3.3.1)

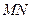саңылауын саңылау қырына параллель болатындай етіп Френель зоналарына бөлінсе, әрбір зонадан шыққан шеткі сәулелердің жүріс айырмасы 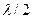болады және зоналар саны 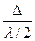болады. Сәулелер саңылауына перпендикуляр түскендіктен жазық толқын майданы саңылау жазықтығына параллель болады. Толқын майданының барлық нүктелері саңылау жазықтығында бірдей фазада тербеледі. Френель зоналарының аудандары бірдей болғандықтан саңылау жазықтығында екінші толқын майданының амплитудалары бірдей болады. (2.3.3.1) формула бойынша зона саны 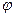бұрышына байланысты. Екінші реттік толқындардың қосылуының нәтижесі зоналарының санына байланысты. Көршілес қос зоналардан шығатын тербелістер бірін-бірі жоятын болғандықтан, интерференциялану нәтижесінде әрбір көршілес қос зонадан келген сәулелердің қорытқы тербеліс амплитудалары нөлге тең болады.

2.3.3.1 -сурет

Сонымен, егер Френель зоналарының саны жұп болса

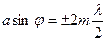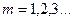; (2.3.3.2)

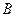нүктесінде дифракциялық минимум болады, ал егер Френель зоналарының саны тақ болса

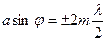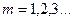; (2.3.3.3)

максимум болады.

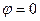болса саңылауда 1 ғана Френель зонасы болады. В нүктесінде орталық дифракциялық максимум байқалады. (2.3.3.2) және (2.3.3.3) формулалары бойынша экранда амплитуда нөлге тең болатын (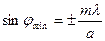) және максимал болатын (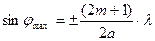) нүктелерді анықтауға болады

Амплитуданың квадраты интенсивтілікті береді. 2.3.3.1,б - суретте экрандағы интенсивтіліктің таралуы (дифракциялық спектр) көрсетілген. Суреттен орталық максимумда жарық энергиясы үлкен болатындығы көрінеді. Егер саңылау кеңдігі 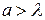болса, онда дифракциялық бейне анық, саны көп бірақ енсіз болады. 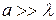болса, экран ортасында жарық көзінің кескіні пайда болады, яғни жарық түзу сызықты таралады. Егер саңылаудың бетін кішірейте берсек, онда дифракциялық бейнелер көмескілене береді. Саңылауға ақ жарық түсірілсе (толқын ұзындықтары әртүрлі 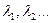), орталық дифракциялық бейне ақ, ал қалған бөліктері боялған болады.

2.3.4 Дифракциялық тордағы Фраунгофер дифракциясы

Дифракциялық тор деп өте дәл құралдың көмегімен ара-қашықтықтары бірдей параллель сызықтар (жолақтар) жүргізілеген мөлдір пластинаны айтады. 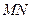және 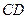екі саңылаудан тұратын дифракциялық торды қарастырайық (2.3.4.1-сурет).

Саңылау кеңдігі 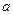, ал екі саңылаудың арақашықтығы 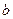, онда 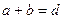дифракциялық тор тұрақтысы немесе периоды делінеді.

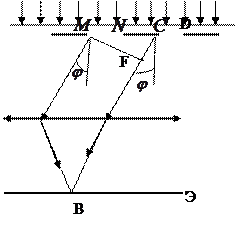
2.3.4.1-сурет

Жазық монохроматты толқын тор жазықтығына перпендикуляр түссін. Саңылаулар бір-бірінен бірдей қашықтықта болғандықтан, көршілес екі саңылаудан сәулелердің жүріс айырмасы 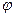бағытында бірдей болады.

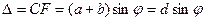(2.3.4.1)

Қосымша минимум шарты

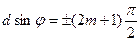
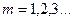(2.3.4.2)

Бас максимум шарты

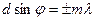
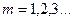(2.3.4.3)

Бас минимум шарты

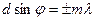
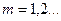(2.3.4.4)

Оптикалық құралдың айыру қабілеттілігі деп өлшемсіз шаманы айтады

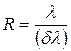(2.3.4.5)

мұнда 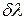- көршілес екі спектрлік сызықтардың толқын ұзындықтарының ең кіші айырымының абсолют шамасы (екі сызық ұзындығы жеке өлшенеді).

Дифракциялық тордың айыру қабілеттілігі. 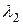толқын ұзындығы үшін максимум шарты

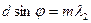
Максимумнан көршілес минимумге өткенде жүріс айырмасы 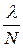-ға өзгереді, 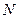– тордағы саңылау саны. 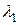үшін (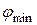бұрышына ауытқиды) минимум шарты

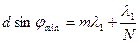
Релей бойынша 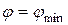, сондықтан

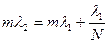
бұдан 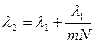немесе сызықтар өте жақын орналасқандықтан

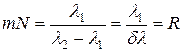(2.3.4.6)

Осыдан дифракциялық тордың айыру қабілеттілігі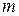спектрдің ретіне және 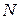саңылау санына тура пропорционал екендігі анықталады. Қазіргі уақыттағы айыру қабілеттілігі өте жоғары (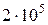) дифракциялық торлар бар.

2.3.5 Кеңістік тор дифракциясы. Вульф-Брегг формуласы

Дифракциялық бейнені бақылау үшін тор тұрақтысы торға түсетін толқын ұзындығымен шамалас болуы керек. Рентген сәулелерінің толқын ұзындығы және кристалдың кеңістіктік торының тұрақтысы шамалас (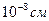). Монохроматты рентген сәулелері (1,2) кристалға 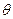бұрышпен сырғанай түссін (2.3.5.1-сурет). Кристалл тор тұрақтысы 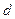. Бұл сәулелер кристалдық тордағы атомдары қоздырады. Бұл атомдар интерференцияланушы когерентті екінші реттік толқындарды (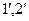) тудырады. Дифракциялық максимумдар атомдардан шағылған барлық толқындар бірдей фазада болғанда бақыланады.

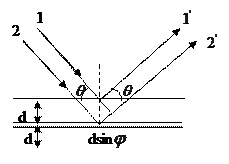
2.3.5.1-сурет

Дифракциялық максимум шарты

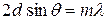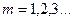, (2.3.5.1)

және Вульф-Бреггтер шарты деп атайды (Г.В. Вульф совет физигі, ал әкелі-балалы Г. және Л. Бреггтер ағылшын физиктері).

Монохроматты рентген сәулелерінің кез-келген түсу бағытында дифракциялық бейне бақыланбайды. Оны бақылау үшін кристалды айналдыра қозғай отырып 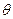ығысу бұрышын алу керек. Немесе кристалғарентген трубкасынан шығатын үздіксіз рентген спектрлерін (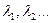) пайдалану қажет, сол кезде (2.3.5.1) шартын осы толқындардың біреуі болмаса біреуі қанағаттандырады.

Рентген сәулелерінің дифракциясы негізгі екі бағытта қолданылады:

1. Рентген сәулелерінің толқын ұзындығы белгілі болғанда 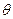және 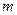өлшей отырып кристалдардың жазықтық аралық қашықтығын (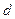), яғни заттың құрылымын анықтауға болады анықтауға болады. Осы әдіс рентгено-құрылымдық сараптау делінеді.Вульф-Брегг формуласы электрондар мен нейтрондардың дифракциясы үшін де дұрыс болады.

2. Кристалдық тордың тұрақтысы белгілі болғанда 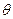және 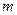-ді өлшей отырып түскен рентген сәулесінің толқын ұзындығын (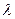) анықтауға болады. Бұл тәсілді рентген-спектроскопия дейді.

2.4 Жарық дисперсиясы

Ортаның сыну көрсеткішінің толқын ұзындығына байланыстылығы жарық дисперсиясы делінеді

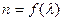(2.4.1)

Жарықтың призмадан өткенде түрлі түсті спектрге ажырауы дисперсия салдарынан болады.

Монохроматты жарық сәулесінің призмадан өтуін қарастырайық. Сыну көрсеткіші 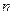призмаға сәуле 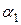бұрышымен түссін (2.4.1-сурет). Призманың екі қырынан шағылған сәуле өзінің бастапқы бағытынан 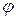бұрышқа ауытқиды. Суреттен

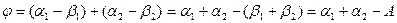
мұнда 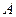– призманың сындыру бұрышы. 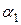мен А бұрыштары кішкене болғандықтан 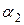және 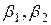бұрыштары да аз шамалы болады. Сондықтан бұл бұрыштардың синустарының орнына олардың мәнін алуға болады: ,,,.

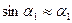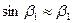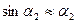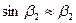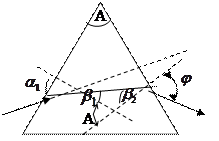
2.4.1-сурет

Сондықтан ; ;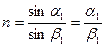

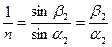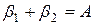
Бұл теңдіктерден 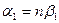; 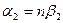, олай болса

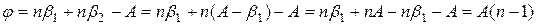(2.4.1)

(2.4.1) формула бойынша ауытқу бұрышы ортаның сыну көрсеткішіне байланысты. Ортаның сыну көрсеткіші толқын ұзындығына байланысты. Осыдан ауытқу бұрышының толқын ұзындығына байланыстылығы шығады. Әртүрлі ұзындықты толқындар әртүрлі ауытқитындықтан призмадан ақ жарық өткенде түрлі түсті спектрге ажырайды. Бұл құбылысты алғаш рет Ньютон бақылаған. Призманың көмегімен де, дифракциялық торды қолданғандай, жарықты спектрге ажырата отырып оның спектральдық құрамын анықтауға болады.

Дифракциялық тор көмегімен толқын ұзындығын төменгі формуладан анықтауға болады

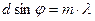
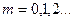
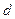– дифракциялық тор тұрақтысы белгілі, 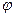ауытқу бұрышын өлшей отырып толқын ұзындығын анықтауға болады. Бұдан 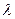үлкен болған сайын 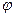бұрышының да үлкен болатындығы көрінеді.

Призмада ақ сәуле ортаның сыну көрсеткіші бойынша спекрге ажырайды. Толқын ұзындығы үлкейген сайын 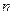кеми береді (2.4.2-сурет).

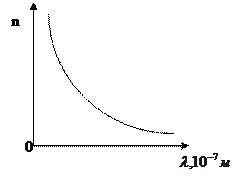
2.4.2-сурет

Сыну көрсеткіші күлгін сәулелерге қарағанда аз болатын қызыл сәулелер призмада азырақ ауытқиды.

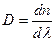шамасы заттың дисперсиясы делінеді. 2.3.6.2-сурет бойынша толқын ұзындығы азайған сайын ортаның сыну көрсеткіші арта береді. Мұндай дисперсия қалыпты дисперсия делінеді. Толқын ұзындығы азайған сайын ортаның сыну көрсеткіші де кеми бастаса оны аномаль дисперсия дейді. Дифракциялық тордың бұрыштық дифракциясы

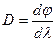. (2.4.2)

2.4.1 Жарықтың дисперсиясының электрондық теориясы

Максвеллдіңі электромагниттік теориясы бойынша ортаның абсолюттік сыні көрсеткіші

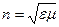(2.4.1.1)

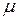- заттың магниттік өтімділігі, 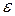- ортаның диэлектрлік өтімділігі, көптеген заттар үшін 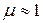, олай болса

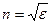. (2.4.1.2)

Осы формула арқылы анықталған сыну көрсеткішінің мәні тәжірибе нәтижелерімен сәйкес келмейді.

Екіншіден 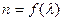формуласы бойынша сыну көрсеткіші айнымалы мәнге ие бола отырып, сонымен қатар (2.4.1.2)-ша белгілі бір тұрақтыға тең. Мұндай ауытқушылықты Лоренц теориясы сәйкестендіреді. Лоренц теориясы бойынша жарық дисперсиясы - электромагниттік толқын мен ортаның зарядталған бөлшектерінің әсерлесуінің нәтижесі: 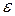ортаның сыну көрсеткіші жарық толқындарының жиілігі 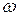-ге байланысты шама болсы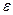н. мен 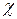арасындағы байластылық

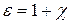
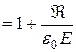
мұнда 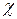-диелектрлік қабілеттілік, 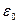– электрлік тұрақты, 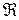- поляризация векторы. (2.4.1.2) бойынша ортаның сыну көрсеткіші поляризация векторына байланысты

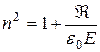(2.4.1.3)

Электр өрісінің әсерінен электрондар еріксіз тербеліске ұшырайды. Электронның диопольдық моменті 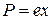, 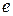– электрон заряды, – жарық толқынының электр өрісінің әсерінен ығысуы. Егер диэлектриктегі атомдардың концентрациясы 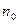болса, поляризацияланудың лездік мәні

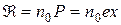(2.4.1.4)

осы формулаларды пайдаланып жазатын болсақ

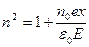(2.4.1.5)

Сол сондықтан электронның сыртқы өріс әсерінен ығысу шамасын анықтау керек. Сыртқы өрістің кернеулігі 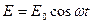бойынша өзгерсін. Еріксіз тербеліс теңдеуі

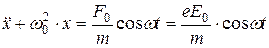(2.4.1.6)

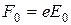– электронға әсер етуші толқындық өріс күшінің амплитудалық мәні, 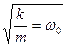– электронның меншікті тербеліс жиілігі. (2.4.1.6) теңдеуінің шешуі

(2.4.1.7)

мұнда 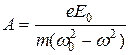(2.4.1.8)

(2.4.1.5) –ға (2.4.1.7)- ны қойғанда

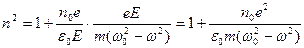(2.4.1.9)

Сонымен 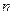сыртқы өріс жиілігіне (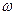) байланысты. 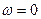-ден 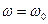-ге дейін 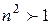және 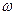артқан сайын артып отырады (қалыпты дисперсия) (2.2.4.1-сурет); 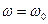болғанда 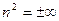; 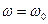- де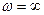н дейін 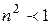және 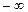-тен 1-ге дейін артады (қалыпты дисперсия).

2.2.4.1-сурет

Үзік сызықтармен көрсетілген 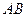қисығы 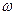артқанда 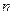кішірейетіндігін көрсетеді (аномаль дисперсия). Бұл уақытта ортаның кедергісі ескерілмейді.

Дата добавления: 2014-10-15