Изоморфизм графов

Матричные способы задания графов

Для алгебраического задания графов используются матри­цы смежности и инцидентности.

Матрица смежностиA = ( a_ij)определяется одинаково для ориентиро­ванного и неориентированного графов. Это квадратная матрица порядка n, где n - число вершин, у которой

a_ij =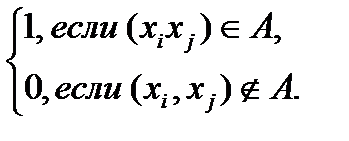

Пример 3.5.

Матрица смежности графа, изображенного на рис. 3.1, имеет вид:

A =

Пример 3.6.

Матрица смежности ориентированного графа, изображенного на рис. 3.2, имеет вид:

A =

Матрица смежности полностью задает граф.

Матрицей инцидентностиB = (b_ij) ориентированного графа называет­ся прямоугольная матрица (n ´ m), где n – число вершин, m – число ребер, у которой

b_i =

Для неориентированного графа матрица инцидентности B задается следующим образом:

b_i =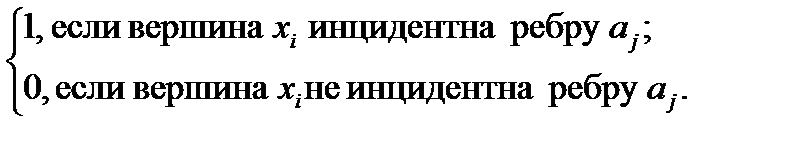

Пример 3.7.

Матрица инцидентности графа, изображенного на рис. 3.1, имеет вид:

B =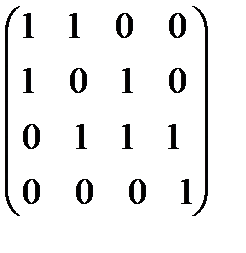

Пример 3.8.

Матрица инцидентности ориентированного графа, изображенного на рис. 3.2, имеет вид:

B =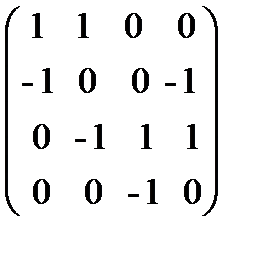

Матрица инцидентности, также, как и матрица смежности, полностью задает граф.

Матрицы смежности и инцидентности удобны для задания графов на ЭВМ.

Основные свойства матриц смежности и инцидентности

1. Матрица смежности неориентированного графа является симметрич­ной. Для ориентированного графа это, вообще говоря, неверно.

2. Сумма элементов i - ой строки или i -го столбца матрицы смежности неориентиро­ванного графа равна степени вершины x_i.

3. Сумма элементов i - ой строки матрицы смежности ориентиро­ванного графа равна числу дуг, исходящих из x_i.

4. Сумма элементов i - го столбца матрицы смежности ориентиро­ванного графа равна числу дуг, входящих в вершину x_i.

5. Сумма строк матрицы инцидентности ориентированного графа явля­ется нулевой строкой.

Итак, возможны следующие различные способы задания графа:

а) посредством графического изображения;

б) указанием множества вершин и множества ребер (дуг);

в) матрицей смежности;

г) матрицей инцидентности.

Графы G ₁= (X ₁, A ₁)и G ₂= (X ₂, A ₂) изоморфны, если существует взаимно однозначное соответствие между множествами вершин X ₁и X ₂, та­кое, что любые две вершины одного графа соединены тогда и только тог­да, когда соответствующие вершины соединены в другом графе.

Пример 3.9

Графы, изображенные на рис. 3.4 являются изоморфными.

Рис. 3.4

Изоморфные графы отличаются только нумерацией вершин. Матрицы смежности двух изоморфных графов могут быть получены одна из другой перестановкой строк и столбцов. Чтобы узнать, являются ли два графа изоморфными, нужно произвести все возможные перестановки строк и столбцов матрицы смежности одного из графов. Если после какой-нибудь перестановки получится матрица смежности второго графа, то эти графы изоморфны. Чтобы убедиться, что графы неизоморфны, надо выполнить все n! возможных перестановок строк и столбцов.

Дата добавления: 2014-11-06