Экстремальные пути в нагруженных ориентированных графах

Ориентированный граф называется нагруженным, если дугам этого графа поставлены в соответствие веса, так что дуге (x_i,x_j)сопоставле­но некоторое число c (x_i,x_j)= c_ij, называемое длиной ( или весом, или стоимостью дуги ). Длиной (или весом или стоимостью) пути s, состоящего из некоторой последовательности дуг (x_i,x_j), называется число l (s), равное сумме длин дуг, входящих в этот путь, т.е.

l (s)= 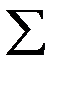c_ij,

причем суммирование ведется по всем дугам(x_i, x_j) 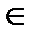s.

Матрица C = (c_ij) называется матрицей длин дуг или матрицей весов.

Рис. 3.10

Для графа, изображенного на рис. 3.10, матрица C имеет вид:

C =

Длина пути (x ₁, x ₂, x ₅, x ₄) равна 1 + 5 + 6 = 12.

Для ненагруженного графа введем понятие кратчайшего пути. Это путь с минимальным общим числом дуг, причем каждая дуга считается столько раз, сколько она содержится в этом пути.

Для нахождения минимального пути между двумя произвольными верши­нами для случая, когда все c_ij ³0 можно воспользоваться простым алгоритмом Дейкстры [2]. В общем случае задача решается с помощью ал­горитмов Флойда, Форда, Беллмана и др. [2,3,5].

Алгоритмы нахождения минимального пути могут быть использованы для поиска кратчайших путей в ориентированном графе без контуров. Для этого нужно каждой дуге приписать вес, равный единице.

3.8 Алгоритм Форда – Беллмана нахождения минимального пути

Дата добавления: 2014-11-06