
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение булевой функции
|
|
|
|
ТЕМА 4. БУЛЕВЫ ФУНКЦИИ
Определение 4.1. Булевой функцией f (x 1, x 2,..., xn) называется произвольная функция n переменных, аргументы которой x 1, x 2,..., xn и сама функция f принимают значения 0 или 1, т. е. xi 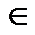 {0, 1}, i = 1, 2,..., n; f (x 1, x 2,..., xn)
{0, 1}, i = 1, 2,..., n; f (x 1, x 2,..., xn) 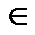 {0, 1}.
{0, 1}.
Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных (их 2 n), а в правой части – значения функции. Пример такого задания представлен в таблице 4.1.
Таблица 4.1
| x 1 x 2 x 3 | f (x 1, x 2, x 3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Для формирования столбца значений переменных удобен лексико-графический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100 = 011+ 1.
Всего существует 22 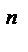 различных булевых функций n переменных.
различных булевых функций n переменных.
Функций одной переменной – 4. Из них выделим функцию “отрицание x ”(обозначается Ø x). Эта функция представлена в таблице 4.2.
 Таблица 4.2
Таблица 4.2
| x | Ø x |
Булевых функций двух переменных – 16 (22 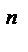 при n = 2). Те из них, которые имеют специальные названия, представлены в таблице 4.3.
при n = 2). Те из них, которые имеют специальные названия, представлены в таблице 4.3.
Таблица 4.3
| x 1 x 2 | x 1V x 2 | x 1& x 2 | x 1 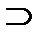 x 2 x 2
| x 1~ x 2 | x 1 Å x 2 | x 1¯ x 2 | x 1ï x 2 |
| 0 0 0 1 1 0 1 1 | 0 | 1 | 1 |
В таблице 4.3 представлены следующие функции двух переменных:
x 1V x 2 – дизъюнкция;
x 1& x 2 – конъюнкция;
x 1É x 2 – импликация;
x 1~ x 2 – эквивалентность;
x 1Å x 2 – сложение по модулю 2;
x 1¯ x 2 – стрелка Пирса;
x 1ï x 2 – штрих Шеффера.
Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!