
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы логики булевых функций
|
|
|
|
Определение 4.2. Формула логики булевых функций определяется индуктивно следующим образом:
1. Любая переменная, а также константы 0 и 1 есть формула.
2. Если A и B – формулы, то Ø A, A V B, A & B, A É B, A ~ B есть формулы.
3. Ничто, кроме указанного в пунктах 1–2, не есть формула.
Пример 4.1.
Выражение (Ø x V y)&((y É z) ~ x) является формулой.
Выражение Ø x & y É z Ø ~ x не является формулой.
Часть формулы, которая сама является формулой, называется подформулой.
Пример 4.2.
x &(y É z) – формула; y É z – ее подформула.
Определение 4.3. Функция f есть суперпозиция функций f 1, f 2,..., fn если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.
Пример 4.3.
f 1 = x 1& x 2 (конъюнкция); f 2 = Ø x (отрицание).
Возможны две суперпозиции:
1) f = f 1(f 2) = (Ø x 1)&(Ø x 2) – конъюнкция отрицаний;
2) f = f 2(f 1) = Ø(x 1& x 2) – отрицание конъюнкции.
Порядок подстановки задается формулой.
Всякая формула задает способ вычисления функции, если известны значения переменных.
Пример 4.4.
Построим таблицу значений функции f (x 1, x 2, x 3) = Ø(x 2 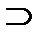 Ø x 3) ~ (Ø x 1V x 2).
Ø x 3) ~ (Ø x 1V x 2).
Таблица 4.4 представляет последовательное вычисление этой функции.
Таблица 4.4
| x 1 x 2 x 3 | Ø x 3 | x 2 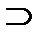 Ø x 3 Ø x 3
| Ø(x 2 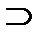 Ø x 3) Ø x 3)
| Ø x 1 | Ø x 1V x 2 | f (x 1, x 2, x 3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций: Ø, &, V, É и ~.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 334; Нарушение авторских прав?; Мы поможем в написании вашей работы!