Лабораторная работа №3. Экстремальные пути в графах 2 страница

3. Привести пример двух бесконечных множеств А и В, таких, что мощность множества А меньше мощности множества В.

4. Нарисовать диаграмму Эйлера-Венна для множества \ .

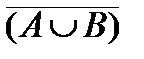5. Эквивалентны ли множество рациональных чисел отрезка [0, 1] и множество рациональных чисел из этого интервала? Ответ обосновать.

Вариант № 29

1. В классе 20 детей. Из них 10 дополнительно занимаются в музыкальной школе, 6 – теннисом, 5 – китайским языком. Музыкальную школу и занятия по теннису посещают три ребенка, музыкой и китайским языком занимаются трое, теннисом и китайским языком двое. Всеми тремя видами дополнительных занятий занимается один ребенок. Сколько детей не занимается ни одним из перечисленных занятий?

2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) Ç ?

3. Доказать, что множество точек A = { y: y = 2ⁿ, n = 1, 2, …} счетно.

4. Нарисовать диаграмму Эйлера-Венна для множества A Ç È Ç B.

5. Эквивалентны ли множества A = {(x, y): y = x ², 1< x <2} и B = {(x, y): y = 2 ^x, 3< x < ¥}?

Вариант № 30

1. В цеху имеется 25 станков, которые могут выполнять три вида операций: А, В и С. Из них 10 станков выполняют операцию А, 15 – В, 12 – С. Операции А и В могут быть выполнены на 6 станках, А и С – на 5, В и С – на 3 станках. Сколько станков могут выполнять все три операции?

2. Верно или неверно равенство: \ = \ ?

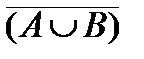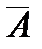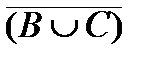3. Привести примеры множеств А, В и С, для которых одновременно выполняются равенства А È В È С = А и А Ç В Ç С = С.

4. Нарисовать диаграмму Эйлера-Венна для множества 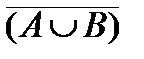Ç С.

5. Можно ли построить взаимно-однозначное соответствие между множеством действительных чисел отрезка [0, 1] и множеством действительных чисел интервала (0, 1)? Ответ обосновать.

2. Раздел «Отношения. Функции»

Вариант № 1

1. Задано бинарное отношение r = {<1, 1>, <1, 3>, <3, 1>, <3, 4>, <4, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не рефлексивного, не симметричного и транзитивного.

3. Дана функция f (x) = x ² + e^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 2

1. Задано бинарное отношение r = {<1, 3>, <3, 1>, <3, 4>, <4, 3>, <4, 4>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не симметричного, но рефлексивного и транзитивного.

3. Дана функция f (x) = x ² + e ^{- x} , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 3

1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 1>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, но рефлексивного и симметричного.

3. Дана функция f (x) = x + e^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 4

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x ² + y ² = 25?

3. Дана функция f (x) = x ³ + e ^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 5

1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <3, 4>, <4, 3>, <4, 4>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не симметричного, не рефлексивного и транзитивного.

3. Дана функция f (x) = x + e ^{-- x} , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 6

1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 1>, <4, 1>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.

3. Дана функция f (x) = x + e ^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 7

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения рефлексивного, симметричного и транзитивного.

3. Дана функция f (x) = x ² + 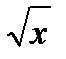, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 8

1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.

3. Дана функция f (x) = x + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 9

1. Задано бинарное отношение r = {<1, 2>, <2, 3>, <1, 3>, <1, 1>, <2, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения транзитивного, рефлексивного и симметричного.

3. Дана функция f (x) = sinx + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 10

1. Задано бинарное отношение r = {<1, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = 2 y?

3. Дана функция f (x) = lnx + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 11

1. Задано бинарное отношение r = {<1, 1>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, инъективной, биективной.

Вариант № 12

1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x + y = 100?

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.

Вариант № 13

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <1, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.

Вариант № 14

1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения рефлексивного, симметричного и транзитивного.

3. Дана функция f (x) = x ² 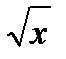, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 15

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения эквивалентности.

3. Дана функция f (x) = x ² + 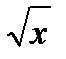, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 16

1. Задано бинарное отношение r = {< b, b >, < b, c >, < c, b >, < c, a >, < d, a >}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения частичного порядка на множестве целых чисел..

3. Дана функция f (x) = x ² + lnx, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 17

1. Задано бинарное отношение r = {< x, x >, < y, z >, < x, z >, < z, x >, < z, y >}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения транзитивного и симметричного.

3. Дана функция f (x) = x + 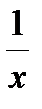, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 18.

1. Задано бинарное отношение r = {<1, 1>, <1, a >, < a, 1>, < a, 4>, <4, a >}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения рефлексивного и транзитивного.

3. Дана функция f (x) = x ² + 2 ^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 19

1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 3>, <3, 2>, <3, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x ² – y ² = 0?

3. Дана функция f (x) = 2 ^x + , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 20

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не рефлексивного, не симметричного и не транзитивного.

3. Дана функция f (x) = x ³ e^x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 21

1. Задано бинарное отношение r = {<1, 3>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения частичного порядка на множестве треугольников на плоскости.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.

Вариант № 22

1. Задано бинарное отношение r = {<1, 2>, <2, 2>, <2, 1>, <2, 3>, <3, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = – y?

3. Дана функция f (x) = lnx + , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 23

1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 3>, <3, 2>, <3, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением частичного полрядка на множестве действительных чисел отношение xry, задаваемое неравенством x ² – y ² £ 0?

3. Дана функция f (x) = e^x + , отображающая множество положительных действительных чисел на множество положительных действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 24

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <3, 2> <1, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество неотрицательных действительных чисел, R ® [0, ¥) и являющейся сюръективной, но не инъективной.

Вариант № 25

1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое неравенством x £ y?

3. Дана функция f (x) = lnx + 2 x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 26

1. Задано бинарное отношение r = {<2, 2>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной и неинъективной.

Вариант № 27

1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством xy = 100?

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.

Вариант № 28

1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <3, 3>, <3, 1>, <1, 3>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.

3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.

Вариант № 29

1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <4, 4>, <2, 1>, <2, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения частичного порядка.

3. Дана функция f (x) = x ² 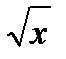, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

Вариант № 30

1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.

Найти D (r), R (r), r r, r ^-1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?

2. Привести пример отношения эквивалентности.

3. Дана функция f (x) = x ² + 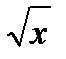, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

3. Раздел «Графы»

1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности).

2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из x ₁ в x ₇ в ориентированном графе, заданном матрицей весов.

3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер.

Варианты заданий

1. 1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14

1 0 0 1 0 0 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 4 6

1 0 0 0 1 0 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 2 ¥ 10 12

0 1 0 0 1 0 ¥ ¥ ¥ ¥ 10 9 ¥ 20 4 10 ¥ 6

1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥

1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11

¥ ¥ ¥ ¥ ¥ ¥ ¥

2. 1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5

0 0 1 1 1 0 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 ¥ 1

0 0 0 0 0 0 ¥ ¥ ¥ 2 ¥ 1 ¥ ¥ 2 ¥ 1 1

1 0 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3

1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥

1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8

¥ ¥ ¥ ¥ ¥ ¥ ¥

3. 1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7

1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3

0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6

1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3

0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 3 6 3 ¥

0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10

Дата добавления: 2014-11-06