Нагрев и охлаждение однородного проводника во времени при продолжительном режиме работы

Если мощность потерь в проводнике при прохождении по нему электрического тока равна Р, то за время dt в нем выделится энергия

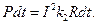(3-9)

Часть этой энергии пойдет на нагревание проводника:

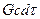, (3-10)

а часть будет отведена в окружающее пространство:

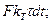(3-11)

здесь G – масса проводника, кг; с – удельная теплоемкость, Дж/(кг·К); F – поверхность теплоотдачи проводника, м²; 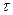τ – превышение температуры проводника по отношению к окружающей среде, °С или К; k _Т – коэффициент теплоотдачи, Вт/(м²·К).

Для любого момента времени будет справедливо следующее уравнение теплового баланса:

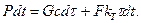(3-12)

Нагрев электрических аппаратов или отдельных их элементов может проходить при следующих основных режимах:

при постоянстве мощности потерь

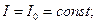
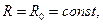
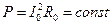(3-13a)

(устройства, у которых сопротивление практически мало меняется от температуры);

при постоянстве тока

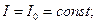
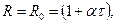
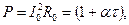(3-13б)

где α – температурный коэффициент сопротивления (силовые цепи почти всех аппаратов, так как ток в цепи определяется нагрузкой; R _{аппарата} << R _{нагрузки});

при постоянстве напряжения

;

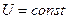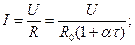
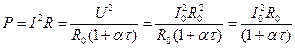(3-14)

(катушки аппаратов).

Если принять с и k _Т постоянными, то при постоянстве мощности решение уравнения (3-14) относительно τ будет

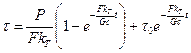, (3-15)

где τ₀ – превышение температуры проводника над температурой среды в момент начала процесса.

В действительности R, с и k _Тзависят от температуры и, следовательно, будут меняться во времени. Погрешность, обусловленную сделанным допущением, можно снизить, если указанные величины принимать не для начальной температуры, а для температуры, близкой к той, которая получится при установившемся режиме.

Величина Gc/F k _Т = Т имеет размерность времени и носит название тепловой постоянной времена нагрева. Физически она представляет собой то время, за которое проводник нагреется до установившейся температуры при отсутствии теплоотдачи в окружающую среду. При t = ∞ уравнение (3-15) принимает вид

τ _{t = ∞} = P/(Fk _Т ) = τ_уст = C, (3-16)

т. е. имеет место установившийся процесс. Выделяемая в проводнике мощность потерь равна мощности, отдаваемой в окружающую среду с поверхности нагретого тела. Уравнение (3-16) носит название формулы Ньютона.

Уравнение

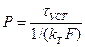(3-16 а)

формально имеет такой же вид, как закон Ома для электрического тока I = U/R. Поэтому величину 1 /(k _Т F) часто называют сопротивлением тепловому потоку при переходе от поверхности F к окружающей среде. Уравнение (3-15) может быть переписано в виде

τ = τ _уст(1 – е ^{– t / T}) + τ ₀ е ^{– t / T}. (3-17)

При τ₀ = 0, т. е. когда процесс начинается с холодного состояния,

τ = τ _уст(1 – е ^{– t / T}). (3-18)

Согласно (3-17) и (3-18) превышение температуры проводника изменяется во времени по закону показательной функции (экспоненты). Установившееся превышение температуры (при t = ∞) в обоих случаях одно и то же и не зависит от величины τ₀.

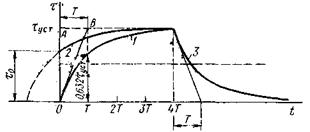
Рис. 3-5. Кривые процесса нагревания и охлаждения однородного проводника при продолжительном режиме работы

На рис. 3-5 приведены кривые 1 и 2, построенные соответственно по уравнениям (3-18) и (3-17). Время t здесь взято в долях Т. Температура τ_уст обычно достигается через время t = (3÷ 5) Т. На рисунке показано графическое определение величины Т. Это будет отрезок АВ на прямой установившегося превышения температуры τ_уст, отсекаемой касательной, проведенной в начале координат к кривой нагревания. Величина T может быть также определена по кривой нагревания на том основании, что за время Т превышение температуры достигает 0,632 τ_уст.

Рассмотрим теперь процесс охлаждения проводника. Допустим, что в какой-то момент времени протекание тока по проводнику прекратилось: Р dt = 0. Проводник начнет охлаждаться. Уравнение (3-14) примет вид

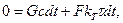(3-19)

откуда

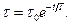(3-20)

Кривая 3 (рис. 3-5) построена по этому уравнению из предположения, что τ₀ = τ_уст. Кривая охлаждения является зеркальным изображением кривой нагревания 2 относительно прямой (проведена штриховой линией), проведенной посредине между осью абсцисс и прямой установившегося превышения температуры. Аналогично предыдущему, только с отсчетом от прямой τ_уст, определится графически величина Т.

Для режима постоянства тока уравнение (3-12) примет вид

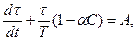(3-21)

где А = 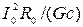представляет собой начальную скорость повышения температуры; С = 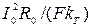– установившаяся температура для режима нагрева при постоянной.мощности, представляющая собой тепловую интенсивность электротермического процесса; T=Gc/(Fk_Т) – тепловая постоянная времени нагрева.

Решение уравнения (3-21) при τ_о = 0 будет

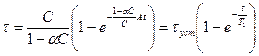(3-22)

где 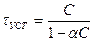– установившееся превышение температуры; 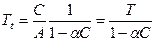– постоянная времени нагрева.

Как видно, в этом режиме в отличие от режима нагрева при постоянной мощности τ_уст и Т_t, в сильной степени зависят от тепловой интенсивности электротермического процесса.

При αС = 1 второй член уравнения (3-21) становится равным нулю, а

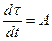(3-23)

откуда

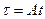(3-24)

т. е. температура нарастает по линейному закону, теоретически до бесконечности, практически до плавления проводника. Установившаяся температура и постоянная времени становятся бесконечно большими (τ_уст = ∞. Т, =∞).

При α С > 1 показатель степени в уравнении (3-22) становится положительным, температура нарастает еще быстрее.

На рис. 3-6 приведены кривые изменения температуры во времени, построенные по уравнению (3-22). Превышение температуры для разных значений α С дано в зависимости от At. Коэффициент α для меди принят равным 1/235.

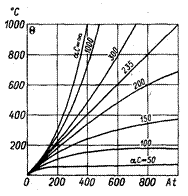
Рис. 3-6. Кривые Θ = f (At)

При постоянстве напряжения уравнение (3-12) напишется в следующем виде:

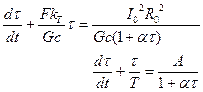(3-25)

Решение этого уравнения получается сложным и громоздким. Ограничимся определением установившихся температуры и тока, представляющих наибольший интерес. При установившейся температуре d τ/ dt = 0, тогда из (3-25)

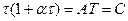(3-26)

и

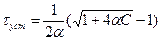(3-27)

При малых τ можно (3-26) решить приближенно, пренебрегая сперва квадратичным членом и используя затем полученный результат для введения поправки. Тогда

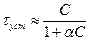(3-27a)

По мере повышения температуры ток уменьшается вследствие увеличения сопротивления и изменяется почти обратно пропорционально сопротивлению:

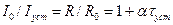(3-28)

Полученные выше результаты для разных режимов могут быть сведены в табл. 3-2.

Дата добавления: 2014-10-15