КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Фізична сторона задачі
|
|
|
|
ЗСУВ
З деформацією зсуву ми зустрічаємося тоді, коли з 6 компонентів головного вектора та головного момента внутрішніх сил відмінні від 0 тільки поперечні сили  та
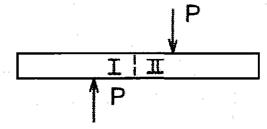
та  Деформацію зсуву можна получити тоді, коли, наприклад, на стержень з протилежнихбоків на дуже близькій відстані одна від одної діють 2 рівні сили, які перпендикулярні до осі бруса та спрямовані в протилежні сторони. Приклад: розріз ножицями полоси:
Деформацію зсуву можна получити тоді, коли, наприклад, на стержень з протилежнихбоків на дуже близькій відстані одна від одної діють 2 рівні сили, які перпендикулярні до осі бруса та спрямовані в протилежні сторони. Приклад: розріз ножицями полоси:
 | |||
 | |||
Запишемо вираз для Q:
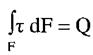
(1), вважаючи що дотичні напруження  рівномірно
рівномірно
розділені по площі поперечного перерізу 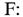 тоді
тоді
 | |||||
 | |||||
 |
 Розглянемо деформаційний елемент:
Розглянемо деформаційний елемент:
 |  | ||
γ- кут зсуву, або відносний зсув
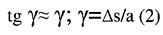 |
Залежність між навантаженням та деформацією зсуву можна простежити
за діаграмою зсуву.
 | |||
 | |||
- границя пружності
 - границя текучості
- границя текучості
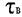 - границя міцності
- границя міцності
Експериментально діаграму зсуву можна зняти при скручуванні труби. Між дотичним напруженням 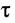 та кутом зсуву
та кутом зсуву 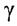 існує лінійна залежність:
існує лінійна залежність:
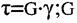 - коефіцієнт пропорційності, який називається модулем пружності
- коефіцієнт пропорційності, який називається модулем пружності
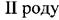
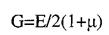 |  | ||
 - закон Гука при зсуві
- закон Гука при зсуві
Умова мiцності при зсуві (зрізі) може бути записана:
 |
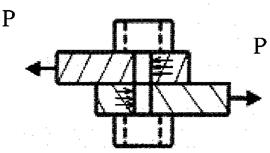 Якщо дотичні напруження розподіленні по перерізу рівномірно, матимемо
Якщо дотичні напруження розподіленні по перерізу рівномірно, матимемо
 | |||
 |
- діаметр болта.
Для болтових та заклепкових з'єднань проводять також розрахунок на зминання:

Fзм – площа зминання
Fзм = δ∙d
σ зм = Р/Fзм = Р/δ∙d ≤ [σ зм] d ≥ Р/δ∙[σ зм]
[σ зм] = (2-2,5) [σ]
Для забезпечення умов міцності на зріз та зминання, треба з двох знайдених діаметрів взяти більший.
Розрахунок зварних з'єднань


Якщо не враховувати напливу, то в перерізі кутовий шов має форму рівнобедреного прямокутного трикутника

a = δ∙cos45° = 0,78
Руйнування шва буде проходити по його мінімальному перерізу висотою
a= 0,78. Розрахункова площа перерізу шва: Fe = a ∙ lт = 0,7∙δ∙l,
де Fe – електрична дуга
Для торцевого шва:
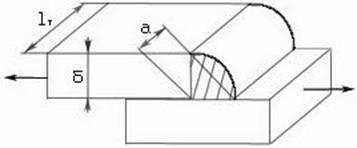
lт – розрахункова довжина торцевого шва
Fе = a ∙ lт = 0,78∙lт
Умова міцності шва: τ = P/Fe ≤ [τe]
Якщо шва два: зверху і знизу, то:

Fe = 2∙a∙lт = 1,4∙δ∙lт Тоді умова міцності
τ = P/Fe = P/1,4∙δ∙lт ≤ [τe]
[τe] – табличне значення;
[τe] = 80 МПа – для ручного зварювання електродами з тонкою обмазкою;
[τe] = 100 Мпа – для автоматичного зварювання та ручного зварювання електродами з товстою обмазкою;
Оскільки на початку та в кінці шва внаслідок непровару його якість погіршується, дійсну його довжину збільшуємо порівняно з розрахунковою на 10мм, тобто:
l = lт + 10мм де l дійсна довжина шва.
Для флангових швів:

Fe = a∙lф = 0,78∙(l – 10), так як їх ставлять паралельно, то:
τ = P / 1,4∙δ∙(l – 10), 1,4 це 0,7∙2
Допустимі напруження при зсуві:
2. За другою теорією міцності: τ = (0,7 ÷ 0,8) ∙ [σ]; τ ≤ [τ]
3. За третьою теорією міцності: τ ≤ [τ] [τ] = 0,5 ∙ [σ]
4. За четвертою теорією міцності: [τ] = 0,6 ∙ [σ]
Лекція №
Тема: „Кручення"
Деформація кручення спричиняються парами сил, площини яких перпендикулярні до осі стержня. Тому при крученні з 6 основних факторів виникає тільки один - крутний момент Мкр. Стержні, які працюють на
кручення звуться валами.

Під дією скручувального моменту, що прикладений на вільному кінці
стержня будь-яки переріз на відстані X від місця закріплення повертається
відносно закріпленого перерізу на кут φ - кут закручування.
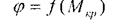 Залежність називаються діаграмами кручення, які
Залежність називаються діаграмами кручення, які
визначають експериментально:
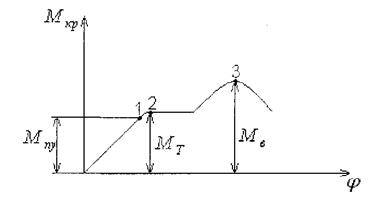 |
Мпу - момент до якого зберігається прямолінійна залежність між
навантаженням та деформацією;
МТ - момент, що відповідає початку текучості;
Мв - крутний момент, який спричинює руйнування вала.
Щоб визначити напруження у поперечних перерізах стержня розглянемо:
1. Статична сторона задачі
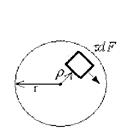 | ||||
 | ||||
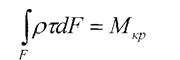 |
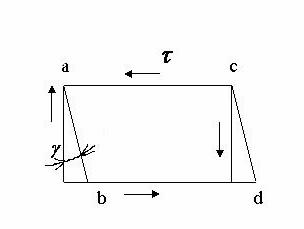
τ- дотичне напруження, яке діє на елементарній площадці dF, розташованій на довільній відстані ρ від центра перерізу.
2. Геометрична сторона задачі
Розглянемо відрізок вала довжиною 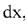 виділений з розглядуваного вала.
виділений з розглядуваного вала.
 | |||
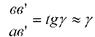 | |||
- кут зсуву на поверхні стержня.
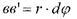
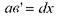

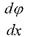 |  | ||
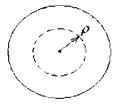
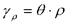

 - відносний кут закручування позначається через, одиниці виміру тоді. Якщо виділити на поверхні елемент радіуса ρ то
- відносний кут закручування позначається через, одиниці виміру тоді. Якщо виділити на поверхні елемент радіуса ρ то
Розглянемо елемент. Елемент перебуває в умовах чистого зсуву, тоді:

Максимальне напруження: 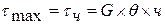
|

 Підставляючи в статичну сторону задачі вираз
Підставляючи в статичну сторону задачі вираз 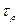

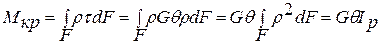 звідси:
звідси:

 - відносний кут закручування
- відносний кут закручування
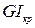 - жорсткість поперечного перерізу стержня
- жорсткість поперечного перерізу стержня
кручення (одиниці виміру 
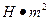 )
)
 - полярний момент інерції.
- полярний момент інерції.
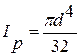 - для суцільного вала.
- для суцільного вала.
Якщо вал трубчастий або полий тоді:
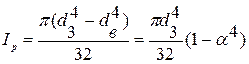 ;
;  .
.
Для визначення взаємного кута закручування двох перерізів, розташованих на відстані l:
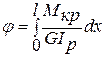
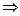

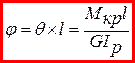 - закон Гука при крученні.
- закон Гука при крученні.
Визначимо дотичне напруження на відстані  :
:
|
|





|

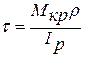
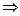


 - полярний момент опору при крученні.
- полярний момент опору при крученні.
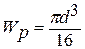 - для суцільного круглого вала.
- для суцільного круглого вала.
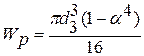 - для трубчастого перерізу.
- для трубчастого перерізу.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 412; Нарушение авторских прав?; Мы поможем в написании вашей работы!