Основные понятия. Поиск более простых процедур кодирования и декодирования привел к появлению циклических кодов

ЦИКЛИЧЕСКИЕ КОДЫ

Поиск более простых процедур кодирования и декодирования привел к появлению циклических кодов.

Циклические коды – линейные блочные коды, обладающие свойством цикличности: если 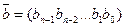- кодовое слово циклического кода, то его циклическая перестановка 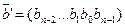также является кодовым словом.

Пример 4.1:

.

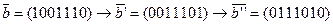Для построения кода достаточно задать одно кодовое слово. Другие кодовые слова образуются из исходного путем циклических перестановок и их линейных преобразований.

Все преобразования кодовых слов циклических кодов производятся в виде математических операций над полиномами (многочленами). Для этого кодовые слова представляются в форме полиномов:

,

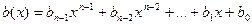где 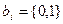- коэффициенты полинома;

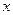- символическая переменная.

Пример 4.2:

.

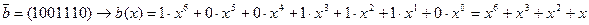Операции сложения, вычитания, умножения и деления полиномов выполняются по обычным арифметическим правилам, только вычитание заменяется сложением, которое производится как сложение по модулю два.

Циклические коды задаются с помощью порождающего (образующего) 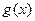и проверочного 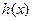полиномов.

Любой полином 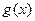степени 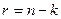, который делит без остатка полином вида 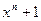, называется порождающим полиномом:

,

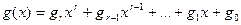где 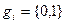- коэффициенты полинома.

Полиномы всех кодовых слов делятся без остатка на порождающий полином.

Порождающая матрица строится на основе полинома .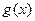

Для несистематического циклического кода:

.

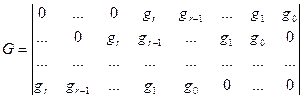Для систематического циклического кода:

,

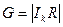где 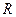- прямоугольная подматрица 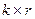, строками которой являются коэффициенты полинома остатка от деления 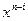на полином 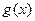, где 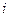- номер строки.

Пример 4.3:

Показать, что полином 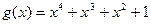является порождающим для 7-разрядного циклического кода. Записать матрицу .

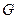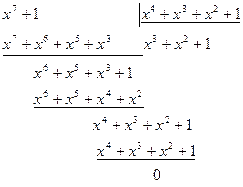
Для несистематического кода:

.

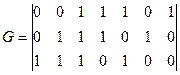Для систематического кода:

.

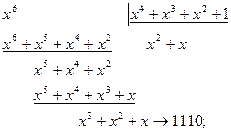
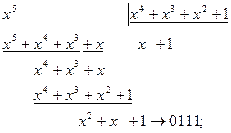
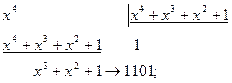
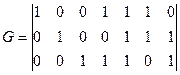Результат деления полинома вида 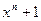на порождающий полином называется проверочным полиномом:

,

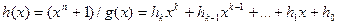где 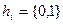- коэффициенты полинома.

При отсутствии ошибок в принятом кодовом слове 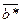остаток от деления произведения 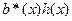на полином вида 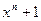равен нулю:

.

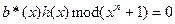Проверочная матрица строится на основе полинома .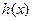

Для несистематического циклического кода:

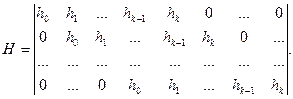
Для систематического циклического кода:

.

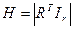ДОМАШНЕЕ ЗАДАНИЕ:

2. Найти полином 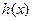для задачи из примера 4.3. Записать матрицу .

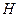Дата добавления: 2014-11-06