Параллельное соединение и его свойства

То есть общее сопротивление последовательного соединения равно сумме сопротивлений ветвей, входящих в соединение

Общая депрессия последовательного соединения равна сумме депрессий всех ветвей, входящих в соединение

Разделим обе части равенства (5.18) на квадрат расхода воздуха q 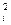=Q²

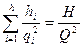(5.19)

В соответствии с равенством (5.11) 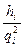=R_i, следовательно, можно записать

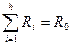(5.20)

Депрессия любой ветви последовательного соединения, как и депрессию всего соединения можно выразить через аэродинамическое сопротивление и расход воздуха т. е.

h_i=R_i*q 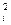(5.21)

H=R₀ Q² (5.22)

Из равенств (5.21), (5.22) q 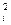=h_i /R_i,и Q² =H/R₀, а так как в последовательном соединении q_i=Q то можно записать

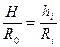(5.23)

Из равенства (5.23) следует

H_i= 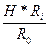(5.24)

В последовательном соединении депрессии отдельных ветвей пропорциональны их сопротивлениям.

Параллельное соединение горных выработок может быть простым (рис.5.9) и сложным (рис.5.10).

Простым параллельным называется такое соединение вентиляционных ветвей, в котором все начала ветвей расходятся в одном узле, а сходятся в другом (рис.5.9).

Сложным параллельным соединением называется такое соединение, когда кроме параллельных ветвей расходящихся в одном узле и сходящимся в другом в этих ветвях имеются дополнительные параллельные ветви (рис.5.10).

Рассмотрим свойства простого параллельного соединения. Согласно определению депрессии разность давления в узлах 1, 2 определяет как депрессию любой ветви входящей в соединение так и депрессию всего соединения, тогда можно записать

Р₁-Р₂=h₁=h₂= =h_i= h_n=H (5.25)

То есть в параллельном соединении депресии всех ветвей одинаковы и равны депрессии всего соединения.

Так как к узлу 1 притекает поток Q, равный общему потоку соединения, а вытекают из него потоки q₁, q₂ q_i q_n, а в узле 2 все наоборот, то в соответствии с первым законом сетей можно записать

Q= 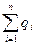(5.26)

Общий поток параллельного соединения равен сумме потоков в отдельных ветвях.

Поток воздуха в любой ветви параллельного соединения, а также общий расход воздуха можно вы разить через депрессию и аэродинамическое сопротивление т. е.

Q= 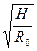(5.27)

q_i= 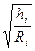(5.28)

С учетом равенств (5.27), (5.28) равенство (5.26) можно записать в виде

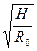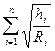= (5.29)

Так как в параллельном соединении Н=h_i, то сократив обе части последнего равенства на 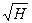получим

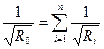(5.30)

Величина обратная корню квадратному из сопротивления называется пропускной способностью, следовательно

K= 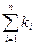(5.31)

То есть общая пропускная способность параллельного соединения равна сумме пропускных способностей ветвей соединения.

Так как К=1/ 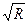, то равенства (5.27), (5.28) можно переписать в виде

Q=K 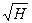(5.32)

q_i=k_i 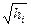(5.33)

Так как в параллельном соединении H=h_i то из равенств (5.32), (5.33) получим,

Q_i= 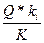(5.34)

Потоки воздуха в отдельных ветвях параллельного соединения пропорциональны пропускной способности этих ветвей.

Теперь целесообразно выписать основные расчетные формулы последовательного и параллельного соединения и сравнить их.

Последовательное соединение	Параллельное соединение
q1=q2= qi= qn=Q	h1=h2= =hi= hn=H
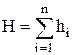
	Q=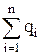
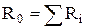
	K=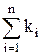
Hi=	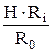Qi=

Дата добавления: 2014-11-06