Вопрос 3. Закон радиоактивного распада. Период полураспада

Отдельные радиоактивные ядра претерпевают превращение независимо друг от друга. Поэтому можно считать, что убыль числа нераспавшихся ядер за малый промежуток времени пропорционально как числу имеющихся ядер 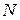, так и промежутку времени :

(23.19)

Разделяя переменные в (23.19), запишем 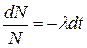; интегрируя полученное дифференциальное уравнение, найдем , потенцируя последнее выражение, получим , откуда при 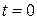находим, что .

Таким образом, получаем закон радиоактивного распада

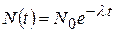, (23.20)

т.е. число нераспавшихся ядер убывает во времени экспоненциально; здесь 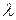– постоянная распада, имеющая смысл вероятности распада ядра за 1 с и равная доле ядер, распадающихся в единицу времени (см. (23.19)).

Закон самопроизвольного радиоактивного распада основывается на двух предположениях: 1) постоянная распада не зависит от внешних условий; 2) число ядер, распадающихся за время dt, пропорционально наличному количеству ядер. Эти предположения означают, что радиоактивный распад является статистическим процессом и распад данного ядра является случайным событием, имеющим определенную вероятность.

Величина является средней продолжительностью жизни (среднее время жизни) радиоактивного изотопа.. Действительно, суммарная

продолжительность жизни dN ядер равна: t | dN |= tλNdt. Средняя продолжительность τ жизни всех первоначально существовавших ядер:

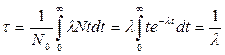. . (23.21)

Характеристикой устойчивости ядер относительно распада является периодполураспада 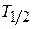– время, в течение которого первоначальное количество ядер данного радиоактивного вещества уменьшается в 2 раза. Это время определяется условием:

, откуда

. (8.22)

Период полураспада – основная величина, характеризующая скорость радиоактивного распада. Чем меньше период полураспада, тем интенсивнее протекает распад. Так, для урана T ≈ 4,5 млрд. лет, а для радия T ≈ 1600 лет. Поэтому активность радия значительно выше, чем урана. Существуют радиоактивные элементы с периодом полураспада в доли секунды. При α- и β-радиоактивном распаде дочернее ядро также может оказаться нестабильным. Поэтому возможны серии последовательных радиоактивных распадов, которые заканчиваются образованием стабильных ядер.

Если дочернее ядро оказывается также радиоактивным, то возникает цепочка радиоактивных превращений. Если происходит цепочка радиоактивных распадов и за время dt из общего числа N м материнских ядер распадается λ м N м dt ядер, а за это же время распадается λ д N д dt дочерних ядер, то общее изменение dN д числа ядер дочернего вещества за единицу времени выразится следующим образом:

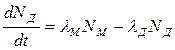. (23.23)

В случае подвижного равновесия между материнским и дочерним

веществами dN д/d t = 0 и выполняется условие радиоактивного равновесия:

. (8.24)

Дата добавления: 2014-11-06