
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 1. Спонтанные и вынужденные переходы между энергетическими уровнями атома. Коэффициенты Эйнштейна
|
|
|
|
Свойства и применения лазерного излучения.
Типы лазеров.
Устройство лазера. Принцип действия лазера.
Взаимодействие света с веществом.
Спонтанные и вынужденные переходы между энергетическими уровнями атома. Коэффициенты Эйнштейна.
ЛЕКЦИЯ 24. ФИЗИКА ЛАЗЕРОВ.
Вопросы:
Основываясь на представлениях Бора о квантовом характере механизма излучения света атомом, Эйнштейн в 1916 г. получил новый вывод формулы Планка, где ввел понятие индуцированного излучения – явления, на котором основан принцип действия лазера.
Состояние частицы или системы частиц в физике можно характеризовать энергией. Из квантовой механики известно, что связанная микрочастица или система микрочастиц может обладать дискретным спектром значений энергии E 1, E 2, E 3,... Количество частиц, находящихся на некотором энергетическом уровне, называют населенностью этого уровня. Как отмечалось выше, состояние частицы с наименьшей энергией и соответствующий энергетический уровень E 1 называют основным, а все остальные − возбужденными уровнями.
В реальных системах микрочастицы, находящиеся при абсолютной температуре Т > 0, вследствие обмена энергией с окружающей средой способны переходить с одного энергетического уровня на другой. Этот скачкообразный переход микрочастиц называется квантовым переходом.
При каждом значении температуры устанавливается динамическое равновесие, характеризуемое постоянным во времени распределением частиц по энергиям. При достаточно высоких температурах, например, для уровней с энергиями Е 1 и Е 2 частицы подчиняются закону распределения Максвелла-Больцмана:
 ,
,  , (24.1)
, (24.1)
где п 2 и n 1– концентрации частиц соответственно на верхнем и нижнем уровнях, Е 2 > Е 1. Избыточная энергия при квантовом переходе с более высокого энергетического уровня на более низкий может передаваться окружающим микрочастицам (безызлучательный переход) или выделяться в виде квантов света. В последнем случае частота ν излучаемого света связана с разностью энергий начального и конечного состояний микрочастицы формулой: hν = E 2 – E 1. В дальнейшем мы не будем учитывать безызлучательные переходы, принимая во внимание лишь переходы с излучением фотонов.
Первоначально считалось, что между энергетическими уровнями атомов происходят два вида переходов: спонтанные и вынужденные.
Спонтанные квантовые переходы атомов с более высоких энергетических уровней на более низкие осуществляются самопроизвольно, то есть без непосредственного воздействия на атомы извне. Эти переходы приводят к спонтанному испусканию фотонов.
Вынужденные переходы атомов с более низких на более высокие уровни происходят в результате поглощение внешнего излучения веществом.
Эйнштейн пришел к выводу, что для объяснения равновесия между излучением и веществом этих двух процессов переходов недостаточно. В самом деле, вероятность спонтанных переходов определяется лишь внутренними свойствами атомов и поэтому не зависит от интенсивности падающего излучения, вероятность же вынужденных переходов с более низких уровней зависит как от свойств атомов, так и от интенсивности падающего излучения. Далее согласно Эйнштейну необходимо учитывать еще третий процесс − переход атомов сболее высоких энергетических уровней на более низкие под воздействием внешнего излучения, в результате которого атомы излучают энергию вынужденно.
Для простоты рассмотрим два энергетических уровня атомов среды, между которыми согласно Эйнштейну возможны три типа процессов: поглощение, спонтанное излучение и вынужденное (индуцированное) излучение (рис. 24.1).


Рис. 24.1
Если атом находится в основном состоянии 1с энергией Е 1, то под действием внешнего излучения может осуществиться вынужденный переход в возбужденное состояние 2 с энергией Е 2, приводящий к поглощению излучения (рис. 24.1,а). Атомы, поглощая свет, переходят на энергетические уровни с большей энергией, причем в соответствии с законом сохранения энергии переход может быть вызван лишь светом определенной частоты. Такой процесс называют резонансным, а также вынужденным (индуцированным) поглощением света.
Атом, находясь в возбужденном состоянии 2, может через некоторый промежуток времени произвольно, без каких-либо внешних воздействий, перейти на более низкий энергетический уровень, отдавая избыточную энергию в виде электромагнитного излучения (испуская фотон с энергией hn=E 2 -E 1). Такие переходы называются спонтанными переходами, а излучение, сопровождающее такие переходы, − спонтанным излучением (рис. 24.1,б). Вследствие случайного характера спонтанных переходов свет, излучаемый микрочастицами, например, атомами, не согласован по фазе, по направлению распространения и поляризации. Следовательно, спонтанное излучение является некогерентным.
Из квантовой механики известно, что возбужденные состояния не являются стабильными. В любой момент микрочастица может с некоторой вероятностью перейти в более низкое возбужденное энергетическое состояние или же в основное, проведя в исходном возбужденном состоянии ограниченное время τ, называемое временем жизни микрочастицы в возбужденном состоянии. Для совокупности микрочастиц вводится понятие среднего времени жизни микрочастицы τ ср в возбужденном состоянии.
Из квантово-механического соотношения Δ E· Δ t ≥ h (Δ E· τ ср ≥ h) следует, что энергия атома в возбужденном состоянии не является строго определенной, т.е. возбужденные энергетические уровни несколько «размыты», причем тем более, чем меньше среднее время жизни этих уровней. В связи с этим частота света, излучаемого при спонтанных квантовых переходах различных атомов, несколько различается, т.е. свет не является строго монохроматическим.
Спонтанное излучение характерно для большинства обычных нелазерных источников света, например, пламён, ламп накаливания, газоразрядных трубок, люминесцентных ламп и др.
Для установления равновесия при произвольной интенсивности падающего излучения необходимы переходы, вероятность которых возрастала бы с увеличением интенсивности излучения, т.е. переходы, связанные с испусканием фотонов под действием излучения. Эйнштейн показал, что помимо поглощения и спонтанного излучения должен существовать третий, качественно иной тип взаимодействия.
Если на атом, находящийся в возбужденном состоянии 2, действует внешнее излучение с частотой, удовлетворяющей условию hn=E 2 -E 1, то возникает вынужденный (индуцированный) переход в основное состояние 1 с излучением фотона той же энергии hn = E 2 - Е 1(рис. 24.1, в).
При подобном переходе происходит излучение атомом фотона дополнительнок тому фотону, под действием которого произошел переход. Возникающее в результате таких переходов излучение называется вынужденным (индуцированным) излучением. Это было весьма важное открытие, которое было реализовано лишь более чем через сорок лет.
Таким образом, в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызывающий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Существенно, что вторичные фотоны неотличимыот первичных, являясь точной их копией.
Вероятность индуцированного испускания будет максимальна, если частота ν воздействующей волны совпадает с частотой перехода (2→1) между уровнями активной среды. При отклонении v от частоты перехода вероятность индуцированного испускания убывает.
В статистической физике известен принцип детального равновесия, согласнокоторому при термодинамическом равновесии каждому процессу можно сопоставить обратный процесс, причем скорость их протекания одинакова. А. Эйнштейн применил этот принцип и закон сохранения энергии для излучения и поглощения электромагнитных волн в случае черного тела.
Для объяснения процессов равновесия между веществом и излучением Эйнштейн показал, что вероятность поглощения фотона атомом зависит не только от состояния атома, но и от спектральной плотности падающего излучения. Вероятность спонтанных переходов зависит только от концентрации возбужденных атомов. Однако, для установления равновесия необходимо также существование переходов из возбужденных уровней на более низкие, вероятность которых зависит от спектральной плотности падающего излучения.
Динамическое равновесие осуществляется посредством постоянного обмена квантами между полем излучения и материальными телами, причем обмен квантами должен уравновешиваться для каждой частоты в отдельности. Поэтому рассмотрим лишь одну частоту. Для других частот все рассуждения будут аналогичными, меняются лишь уровни энергии атомов.
Установим количественные соотношения, связывающие населенности уровней энергии системы частиц, спектральную плотность энергии электромагнитного излучения, падающего на систему, вероятности спонтанного и вынужденного излучений и резонансного поглощения частиц системы.
Электромагнитное излучение в вакууме характеризуется полной объемной плотностью энергии излучения, состоящей из электрической и магнитной составляющих:
 . (24.2)
. (24.2)
Объемная плотность энергии излучения определенным образом распределена по спектру частот. Распределение энергии излучения по частотам описывается спектральной плотностью энергии излучения w (ν, T), равной отношению плотности энергии dw в интервале частот от ν до ν + dν к частотному интервалу dν:
 . (24.3)
. (24.3)
Так как из формулы (24.3) следует соотношение dw = w (ν, T) dν, то для вычисления интегральной плотности энергии во всем частотном диапазоне следует проинтегрировать его по всем частотам, т.е.
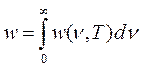 . (24.4)
. (24.4)
Эйнштейн применил к описанию процессов спонтанного и вынужденного излучения вероятностные методы.
Если количество переходов атомов с верхнего уровня на нижний спонтанно равно 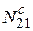 , вынужденно –
, вынужденно –  , с нижнего уровня на верхний вынужденно равно
, с нижнего уровня на верхний вынужденно равно  , то условие термодинамического равновесия запишется в виде
, то условие термодинамического равновесия запишется в виде
 . (24.5)
. (24.5)
Пусть А 21 – вероятность спонтанного перехода ( ) в секунду, п 2 и n 1– концентрации атомов соответственно на верхнем и нижнем уровнях. Тогда
) в секунду, п 2 и n 1– концентрации атомов соответственно на верхнем и нижнем уровнях. Тогда
 . (24.6)
. (24.6)
Количество вынужденных переходов пропорционально спектральной плотности излучения. Обозначим вероятности вынужденных переходов в секунду ( и
и 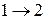 ) соответственно величинами
) соответственно величинами  и
и  , которые относятся к спектральной плотности излучения
, которые относятся к спектральной плотности излучения  , тогда
, тогда
 ,
, 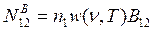 . (24.7)
. (24.7)
С учетом (24.6) и (24.7) соотношение (24.5) примет вид:
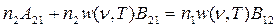 . (24.8)
. (24.8)
Подставляя (24.1) в (24.8) и сокращая полученное выражение на общий множитель п 0, находим:
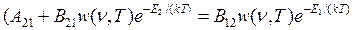 . (24.9)
. (24.9)
Величины А 21, В 21, В 12 называются коэффициентами Эйнштейна. Они являются характеристиками только самого атома и могут зависеть лишь от частоты  . Для установления связи между коэффициентами Эйнштейна исследуем асимптотическое поведение выражения (24.9) при Т→∞. Из физических соображений полагают, что при
. Для установления связи между коэффициентами Эйнштейна исследуем асимптотическое поведение выражения (24.9) при Т→∞. Из физических соображений полагают, что при  величина w (ν, T) → ∞, поэтому
величина w (ν, T) → ∞, поэтому  и слагаемым A 21 в скобках можно пренебречь. Кроме того,
и слагаемым A 21 в скобках можно пренебречь. Кроме того, 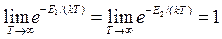 . В результате равенство (24.9) примет вид:
. В результате равенство (24.9) примет вид:
 .
.
После сокращения последнего равенства на w (ν, T) получаем первое соотношение между коэффициентами Эйнштейна:
 . (24.10)
. (24.10)
Физический смысл этого соотношения заключается в том, что при постоянной спектральной плотности энергии w (ν,T) вероятность индуцированного излучения кванта света атомом равна вероятности резонансного поглощения кванта света этим же атомом за одинаковые промежутки времени.
Для вычисления спектральной плотности энергии w (ν, T) умножим соотношение (24.9) на множитель  . После последующего преобразования и с учетом (24.10) получим:
. После последующего преобразования и с учетом (24.10) получим:
 , (24.11)
, (24.11)
где 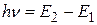 .
.
Для определения отношения коэффициентов Эйнштейна А 21/ В 21 используем формулу Рэлея – Джинса, хорошо описывающую поведение излучения в предельном случае hν << kT:
 .
.
В рассматриваемом предельном случае выражение 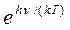
 разложим в ряд Тейлора по степеням
разложим в ряд Тейлора по степеням  , ограничившись в разложении двумя первыми слагаемыми:
, ограничившись в разложении двумя первыми слагаемыми:  , тогда (24.11) запишется в виде:
, тогда (24.11) запишется в виде:
 . (24.12)
. (24.12)
Формула Рэлея – Джинса для спектральной плотности излучения в случае малых частот имеет вид:
 . (24.13)
. (24.13)
Сравнивая выражения (24.11) и (24.13), находим второе соотношение между коэффициентами Эйнштейна:
 . (24.14)
. (24.14)
Формула (24.11) принимает вид
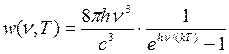 (24.15)
(24.15)
и совпадает с формулой Планка для спектральной плотности излучения.
Хотя элементарная квантовая теория излучения абсолютно черного тела не позволяет теоретически вычислить значения коэффициентов Эйнштейна, она демонстрирует необходимость существования спонтанных и вынужденных переходов, причем, для вероятностей вынужденных переходов имеет место важное соотношение (9.10).
Кванты, испущенные в результате вынужденных переходов, коррелируют по своим свойствам с излучением, которое вызывает эти переходы. Вынужденное излучение обладает той же поляризацией, тем же направлением распространения и той же фазой, что и вынуждающее переход излучение. Это свойство вынужденного излучения чрезвычайно важно для различных его применений.
Были созданы когерентно излучающие источники, в которых различные атомы вещества излучают кванты света согласованно, т.е. с одинаковыми частотами, фазами, поляризацией и направлениями распространения. Они называются оптическими квантовыми генераторами или лазерами. Слово "лазер" образовалось из первых букв полного английского выражения "light amplification by stimulated emission of radiation", что в переводе означает: усиление света посредством стимулированного излучения.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 2209; Нарушение авторских прав?; Мы поможем в написании вашей работы!