Дифференциальные уравнения первого порядка

Дифференциальные уравнения, их порядок, общий и частные интегралы

Дифференциальным уравнениемназывается равенство, содержащее производные или дифференциалы неизвестной функции.

Если неизвестная функция зависит только от одного аргумента, то дифференциальное уравнение называется обыкновенным, а если она зависит от нескольких аргументов и дифференциальное уравнение содержит ее частные производные по этим аргументам, то оно называется уравнением с частными производными.

Будем рассматривать обыкновенные дифференциальные уравнения.

Порядком дифференциального уравнения называется порядок высшей производной, содержащейся в этом уравнении.

Функция, удовлетворяющая дифференциальному уравнению, т.е. обращающая его в тождество, называется интегралом (решением) данного уравнения.

Интеграл дифференциального уравнения, называется общим, если он содержит столько независимых произвольных постоянных, каков порядокуравнения. А функции, получаемые из общего интеграла при различных числовых значениях произвольных постоянных, называются частными интегралами этого уравнения.

Отыскание частного интеграла дифференциального уравнения, удовлетворяющего начальным условиям, называется задачей Коши.

Уравнение с разделенными переменными.

Общий вид: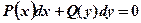

Его общий интеграл: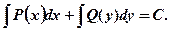

Уравнение с разделяющимися переменными.

Его общий вид: или .

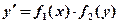Разделяя переменные: 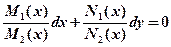, получаем дифференциальное уравнение с разделенными переменными.

Однородное дифференциальное уравнение первого порядка.

Это уравнение вида: 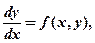если функция 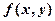удовлетворяет условию , k=const

Уравнение первого порядка 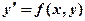называется однородным, если 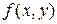можно представить как функцию только одного отношения переменных 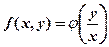, т.е. уравнения вида .

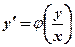Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой у=ux (или x=uy), где u=u (x) (u=u (y))- новая функция.

Пример 1.

Найти общий интеграл данного уравнения:

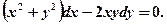
Решение:

Это однородное уравнение, т.к.

Далее вводим новую функцию 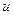, полагая 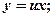при этом 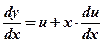и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными 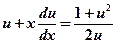или

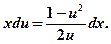
Разделим переменные: 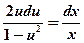и, интегрируя, найдем 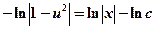или 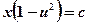. Исключая вспомогательную функцию 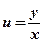, окончательно получим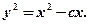

Линейные уравнения первого порядка

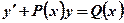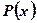Это уравнения вида: , где и 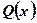- известные функции от х.

Посредством замены функции 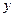произведением двух вспомогательных функций 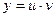линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.

Пример 2

Решить уравнение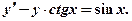

Решение:

Убедившись, что данное уравнение линейное, полагаем 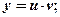тогда 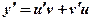и данное уравнение преобразуется к виду:

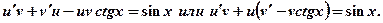
Так как одну из вспомогательных функци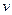й или 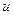можно взять произвольно, то выберем в качестве 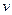какой – либо частный интеграл уравнения 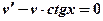(1)

Тогда для отыскания 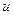получим уравнение: 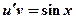(2)

Решая первое уравнение, найдем 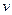. Разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:

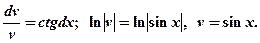
Подставляя v во второе уравнение и решая его, найдем 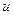как общий интеграл этого уравнения: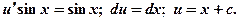

Зная 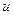и 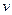, находим искомую функцию .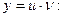

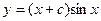Уравнение Бернулли

Его общий вид: 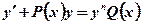. Данное уравнение отличается от линейного тем, что в правую часть входит множителем некоторая степень функции 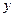. Решается оно так же, как и линейное. Посредством подстановки 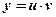сводится к двум уравнениям с разделяющимися переменными.

Дата добавления: 2014-11-06