
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производные старших порядков
|
|
|
|
Использование дифференциала для приближенных вычислений.
Так как 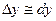 при малых
при малых 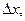 т.е.
т.е. 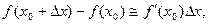 то
то
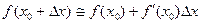 . (1)
. (1)
Эта формула позволяет находить приближенные значения 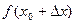 при малых
при малых 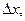 если известны
если известны 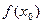 и
и 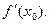 При этом погрешность при замене
При этом погрешность при замене 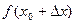 правой частью формулы (1) тем меньше, чем меньше
правой частью формулы (1) тем меньше, чем меньше 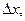 и, более того, эта погрешность при
и, более того, эта погрешность при 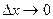 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 
Пример 1. Вычислить приближенное значение 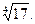
Решение. Будем рассматривать 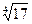 как частное значение функции
как частное значение функции 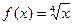 при
при 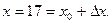 Пусть
Пусть 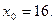 Тогда
Тогда 
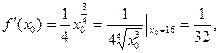
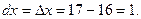 Подставляя в формулу (1), получим
Подставляя в формулу (1), получим

Предположим, что функция 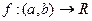 дифференцируема на интервале
дифференцируема на интервале 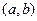 , т.е. " x Î(a, b)
, т.е. " x Î(a, b)  .Определим на интервале
.Определим на интервале 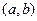 функцию g равенством: g (x)=
функцию g равенством: g (x)= 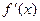 .
.
Определение 1. Если в точке 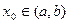 существует производная
существует производная 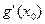 функции g, то эта производная называется производной второго порядка функции
функции g, то эта производная называется производной второго порядка функции 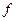 в точке
в точке  и обозначается одним из символов:
и обозначается одним из символов:

Если производная порядка n 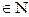 определена (ее обозначение
определена (ее обозначение 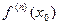 или
или 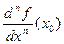 ), и для любого
), и для любого 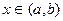 существует
существует 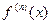 , то производная в точке
, то производная в точке  порядка (n +1) определяется как
порядка (n +1) определяется как 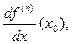 если последняя существует.
если последняя существует.
Пример 1. Пусть 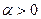 . Тогда для
. Тогда для  и
и 
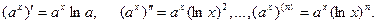
В частности,

Пример 2. Для  и
и 
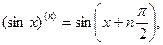
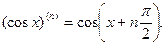
Пример 3. Пусть aÎ 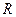 . Для
. Для  и
и 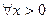
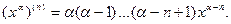
В частности, для 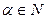 и
и  ,
, 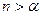
 " x Î
" x Î 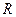 .
.
Пример 4. Для  и
и 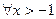
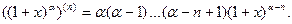
Пример 5. Для  и
и 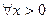
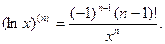
Далее полагаем

Теорема 1. Предположим, что функции f и g имеют на (a, b) производные порядка n. Тогда:
1) 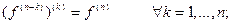
2) 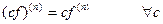 ;
;
3) 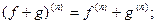
4) 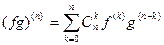 (Формула Лейбница).
(Формула Лейбница).
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 756; Нарушение авторских прав?; Мы поможем в написании вашей работы!