
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило Лопиталя
|
|
|
|
Правила вычисления пределов функций в точке применимы при определенных ограничениях. В ряде важных случаев представляет интерес вычисление пределов при условиях, в которых упомянутые ограничения не выполняются. Типичным является вопрос о пределе при  в одной из следующих ситуаций:
в одной из следующих ситуаций:
 , когда
, когда 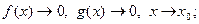
 , когда
, когда 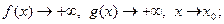
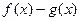 , когда
, когда 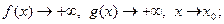
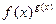 , когда
, когда 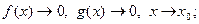
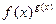 , когда
, когда 
Эффективным средством вычисления подобных пределов является использование понятия производной. Правила вычисления таких пределов были впервые предложены Гийомом Франсуа де Лопиталем (1661-1704) –французским математиком, автором первого учебника по дифференциальному исчислению (1696).
Теорема 1. Предположим, что функции 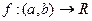 и
и 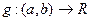 удовлетворяют условиям:
удовлетворяют условиям:
1) 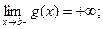
2) 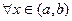 существуют
существуют 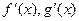 ;
;
3) 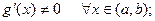
4) существует
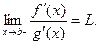
Тогда существует
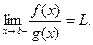
Аналогичная теорема имеет место для предела справа.
Пример 1. Покажем, что 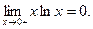 Положим
Положим  Тогда
Тогда 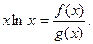 Для этих функций
Для этих функций 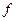 и
и 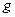 условия Теоремы 1 выполнены, поэтому
условия Теоремы 1 выполнены, поэтому
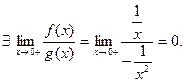
Пример 2. Покажем, что

Положим 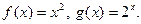 Для функций
Для функций 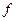 и
и 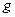 условия 1)-3) Теоремы 1 выполнены. Чтобы выяснить, будет ли выполнено условия 4) надо Теорему 1 применить к функциям
условия 1)-3) Теоремы 1 выполнены. Чтобы выяснить, будет ли выполнено условия 4) надо Теорему 1 применить к функциям 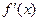 и
и 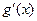 . Так как для них условия 1)-4) Теоремы 1 выполнены, то
. Так как для них условия 1)-4) Теоремы 1 выполнены, то

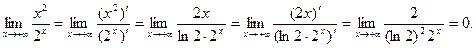
Теорема 2. Предположим, что функции 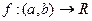 и
и 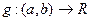 удовлетворяют условиям:
удовлетворяют условиям:
1) 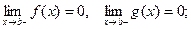
2) 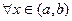 существуют
существуют 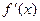 и
и 
3) 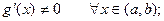
4) существует
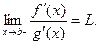
Тогда существует

Пример 3. Пусть  . Докажем, что
. Докажем, что
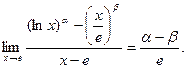
Положим

и применим Теорему 2. Условия 1) -3) Теоремы 2 выполнены и, кроме того,
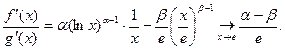
Пример 4. Доказать, что

Решение. Согласно определению степенно-показательной функции

По Теореме 2


Поэтому
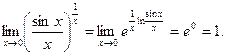

12) Исследование выпуклости.
Пусть  .
.
Определение 1. Функция 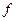 называется выпуклой вниз на
называется выпуклой вниз на  , если
, если 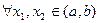 и
и 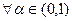 выполняется неравенство
выполняется неравенство
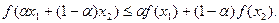
Функция 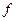 называется выпуклой вверх на
называется выпуклой вверх на  , если функция -
, если функция - 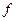 выпукла вниз на
выпукла вниз на  .
.
Определение 2. Функция 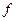 называется строго выпуклой вниз на
называется строго выпуклой вниз на  , если
, если
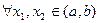 ,
, 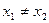 и
и 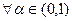 выполняется неравенство
выполняется неравенство

Функция 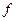 называется строго выпуклой вверх на
называется строго выпуклой вверх на  , если функция -
, если функция - 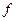 строго выпукла вниз на
строго выпукла вниз на  .
.
Функция, удовлетворяющая одному из приведенных определений, называется выпуклой.
Пример 1. Функция 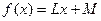 выпукла вниз и выпукла вверх (но не строго) на всей числовой оси.
выпукла вниз и выпукла вверх (но не строго) на всей числовой оси.
Пример 2 Функция 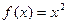 строго выпукла вниз на всей числовой оси. Действительно, пусть
строго выпукла вниз на всей числовой оси. Действительно, пусть 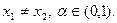 Тогда
Тогда


Теорема 1. Пусть 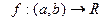 и
и 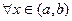 существует
существует  .
.
1) Для того чтобы функция 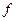 была выпуклой вниз на
была выпуклой вниз на  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 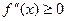
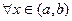 .
.
2) Для того, чтобы функция 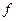 была строго выпуклой вниз на
была строго выпуклой вниз на  , необходимо и достаточно, чтобы:
, необходимо и достаточно, чтобы:
a) 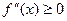
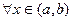 ;
;
b) не существовало интервала  такого, что
такого, что 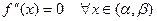 .
.
13) Условия локального экстремума.
Определение 1. Пусть  . Точка
. Точка 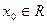 называется точкой локального максимума функции
называется точкой локального максимума функции 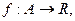 , если
, если
 и
и 
При этом точка  называется точкой строгого локального максимума, если
называется точкой строгого локального максимума, если

Аналогично определяются точки локального минимума и строгого локального минимума. Точки локального минимума и локального максимума называются точками локального экстремума.
Теорема 1. Пусть  есть точка локального экстремума функции
есть точка локального экстремума функции 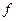 . Если
. Если 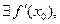 то
то 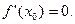
Определение 2. Точки, в которых производная функции 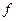 обращается в нуль, называются критическими (стационарными) точками функции
обращается в нуль, называются критическими (стационарными) точками функции 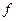 .
.
Говорят, что функция 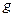 сохраняет знак левее точки
сохраняет знак левее точки  , если
, если
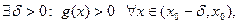
либо

Аналогично определяется понятие “функция 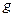 сохраняет знак правее точки
сохраняет знак правее точки  ”.
”.
Теорема 2. Пусть 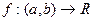 удовлетворяет одному из следующих двух условий:
удовлетворяет одному из следующих двух условий:
1)  причем точка
причем точка  критическая и производная
критическая и производная 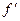 сохраняет знак правее и левее точки
сохраняет знак правее и левее точки  ;
;
2) 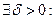
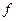 непрерывна на
непрерывна на  , дифференцируема в каждой точке
, дифференцируема в каждой точке 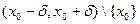 и производная
и производная 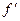 сохраняет знак правее и левее точки
сохраняет знак правее и левее точки  .
.
Если при переходе через точку  производная
производная 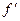 меняет знак, то
меняет знак, то  есть точка локального экстремума. Если при переходе через точку
есть точка локального экстремума. Если при переходе через точку  производная
производная 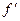 знака не меняет, то
знака не меняет, то  не является точкой локального экстремума.
не является точкой локального экстремума.
Теорема 3. Пусть  . Предположим, что выполнены условия:
. Предположим, что выполнены условия:
1) 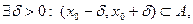 и
и 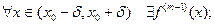
2) 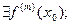
3) 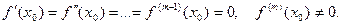
Тогда для  точка
точка  есть точка локального экстремума. Именно, точка локального максимума при
есть точка локального экстремума. Именно, точка локального максимума при 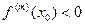 и точка локального минимума при
и точка локального минимума при  . Для значений
. Для значений  точка
точка  не является точкой локального экстремума.
не является точкой локального экстремума.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!