Эталоны решения типовых задач

Задача №1. Построить график функции у=х³-3х.

При построении графиков функций удобно действовать по следующей схеме:

1. найти область определения функции;

2. установить, обладает ли функция симметрий (исследовать функцию на четность);

3. исследовать функцию на непрерывность, периодичность;

4. рассмотреть поведение функции в окрестностях точек разрыва;

5. определить поведение функции в бесконечности;

6. найти точки пересечения графика функции с осями координат, если это возможно (хотя бы приближенно);

7. найти интервалы возрастания, убывания и точки экстремума функции;

8. определить точки перегиба;

9. определить интервалы выпуклости и вогнутности;

10. составить сводную таблицу и построить график.

В ходе построения графика по мере необходимости можно получить допольнительно ряд значений функции при некоторых частных значениях аргумента х, т.е. еще ряд точек графика. Разумеется, в процессе исследования функции не обязательно строго придерживаться приведенной схемы, иногда даже удобно изменить порядок действий.

Решение.

1. Функция определена при всех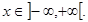

2. На концах интервала lim (x³-3x)=-¥; lim (x³-3x)=+¥,

x® -¥ x®+¥

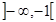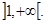3. Определим интервалы возрастания и убывания функции. Функция возрастает на интервале, если f ^¢(x)>0. В данном случае f ^¢(x)=3х²-3>0, если х²>1 или |х|> 1. Следовательно, функция у=х²-3х возрастает на интервалах и Функция убывает на интервале, если f ^¢(x)<0: 3х²-3<0, откуда х²<1, или -1<х<1. Следовательно, функция у=х³-3х убывает на интервале ]-1, 1[.

4. Определим критические точки и исследуем их характер. Из условия 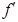(x)=3x²-3=0 найдем критические точки: х₁=-1, х₂=1. Определим знак первой призводной в окрестностях точек х₁=-1, х₂=1. Для точки х₁=-1 имеем 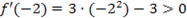, f ^¢(x)=3·0²-3<0. Так как знак производной при переходе через критическую точку х=-1 изменился с плюса на минус, то х=-1 это точка максимума. Максимум функции f(-1)=(-1)³-3(-1)=2 (точка А на рис. 4). Для точки х₂=1 имеем 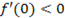, 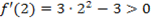. Так как знак производной при переходе через критическую точку изменился с минуса на плюс, то х=1 это точка минимума. Минимум функции 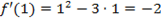(точка В на рис. 4).

5. Определим точку перегиба: 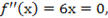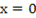. Ордината точки перегиба f(0)=0³-3·0=0 (точка О на рис. 4).

6. Определим интервалы выпуклости и вогнутности. Кривая выпукла при условии 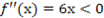, откуда х<0. Следовательно, кривая выпукла на интервале 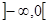. Кривая вогнута при условии 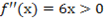, откуда х>0. Следовательно, кривая вогнута на интервале .

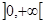7. Найдем точки пересечения кривой с осью Ох. Из системы уравнений находим точки пересечения:

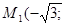0); О (0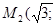; 0), 0).

8. Сведем результаты исследования в таблицу:

х	-1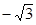
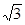
f(x)			-2
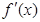
		-3
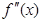
	-6
Характер точки	Максимум	Перегиб	Минимум

9. Строим график функции у=х³-3х

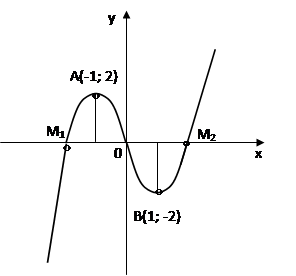Рис 4. График функции у=х³-3х.

Задача 2. Установить, при каком процентом содержании у кислорода в газовой смеси скорость окисления азота будет максимальной, если уравнение кинетики имеет вид 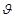=k(100x²-x³), где k -постоянная, х -концентрация окиси азота и х+у=100.

Решение. Найдем производную функции 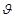и приравняем ее нулю: 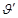= k(200х-3х²)=0, откуда критические точки х₁=0, х₂=200/3. Исследуем точку х₁=0: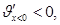 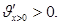В точке х₁=0 функция 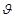имеет минимум. Исследуем точку х₂=200/3: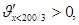 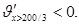Следовательно, х₂=200/3 – точка максимума функции 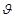, и поэтому у₂=100-200/3=33,3. Скорость окисления будет максимальной в том случае, когда в смеси будет содержаться 33,3% кислорода.

Задача 2. Реакция организма на введенный лекарственный препарат может выражаться в понижении температуры, повышении давления и т.д. Степень реакции зависит от назначенной дозы лекарства. Пусть х обозначает дозу назначенного лекарственного препарата, а степень реакции описывается функцией у=f(x)=x²(a-x), где а -положительная постоянная. При каком значении х реакция максимальна?

Решение. Найдем производную функции и приравняем ее к нулю: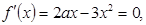откуда критические точки х₁=0, х₂=2а/3.

Значение х₁=0 указывает на то, что в организм лекарство не вводилось. Исследуем точку х₂=2а/3: 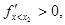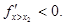Следовательно, в точке х₂=2а/3 функция имеет максимум. Таким образом, х=2а/3 – это доза, которая вызывает максимальную реакцию.

Дата добавления: 2014-10-15