Спектральный анализ периодических сигналов

Периодическим называется сигнал, значение которого повторяется через определенные интервалы времени, которые называют периодом сигнала и обычно обозначают буквой Т.

Простейшие периодические сигналы основаны на функциях косинуса или синуса.

,

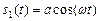где ω – круговая частота,

,

Одно из простейших гармонических колебаний – это сумма колебаний синуса и косинуса. В данном случае частота одинакова для обоих слагаемых.

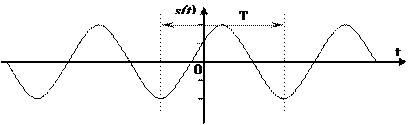
Начало координат в данном случае может располагаться произвольно.

Сложим колебания:

На рисунке показан результат сложения двух сигналов: f₁ = 600 Гц, f₂ = 1000 Гц.

Сдвиг между фазами φ = 45°, одно деление (клеточка) = 1мс.

Фурье в 20 гг. XIX века доказал, что любой периодический сигнал можно представить в виде разложения на гармонические (составляющие) колебания

,

где Т – период,

,

.

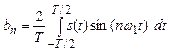Если сигнал описывается четной функцией времени (s(-t) = s(t )), то тогда все коэффициенты b_n равны нулю и можно записать, что

Если сигнал s(t) описывается нечетной функцией времени (s(-t) = - s(t )), то тогда все коэффициенты a_n равны нулю и можно записать, что

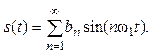
В общем случае, когда сигнал произвольный, используют другую, более удобную форму записи ряда Фурье:

Формулы для нахождения a_n и b_n остаются такие же:

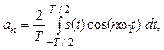
Это представление называют спектральным, или частотным, представлением сигнала. Спектральное представление сигнала - это постоянная составляющая (А₀/ 2) и бесконечное число гармонических составляющих (гармонических сигналов). Число n определяет порядковый номер гармоники. Каждая гармоника характеризуется амплитудой A_n, частотой n ω₁ и начальной фазой φ_n∙ Гармоника, соответствующая n = 1 – это первая (основная) гармоника. Она имеет частоту, равную частоте сигнала.

Совокупность всех амплитуд гармоник A_n определяет амплитудный спектр сигнала, а совокупность всех начальных фаз называется фазовым спектром сигнала.

Графическое изображение спектра называется спектральной диаграммой. Пример амплитудной спектральной диаграммы.

Пример фазовой спектральной диаграммы.

Графический спектр состоит из отдельных линий, и поэтому он называется линейчатым. Расстояния между гармониками равны основной частоте (чаще бывает так, что какая-либо гармоника равна нулю, и кажется, что расстояние между гармониками разное). На самом деле, это не так и гармонику, равную нулю, тоже необходимо считать (см. пример ниже). Спектр периодического сигнала называют также дискретным, поскольку гармоники определены на дискретных частотах ω₁, 2ω₁, 3ω₁ …

Дата добавления: 2014-11-06