Построение графиков. Mathcad позволяет легко создать и затем отформатировать график функции, заданной для дискретного аргумента

Mathcad позволяет легко создать и затем отформатировать график функции, заданной для дискретного аргумента.

Рассмотрим построение графика на предыдущем примере функции y(x) = sin (x) (см. рис. 11). После задания диапазона изменения дискретного аргумента и определения функции для создания графика нужно выполнить следующие действия:

1) установить визир в месте размещения графика и выполнить команду меню Графика → Декартов график или щелкнуть кнопку палитры графиков. В результате в документе появится графическая область с незаполненными полями (рис. 12);

Рис. 12. Графическая область с незаполненными полями

2) в поле графика под осью абсцисс посередине задать имя дискретного аргумента x;

3) в поле графика слева от оси ординат посередине задать функцию y(x), для которой требуется построить график.

После щелчка на любом свободном месте вне графика Mathcad вычисляет и строит точки графика и устанавливает пределы по осям координат.

При построении графиков следует соблюдать те же правила размещения переменных, что и при вычислениях, т. е. исходные данные для графика должны быть записаны выше или слева от него.

Для построения нескольких графиков в одних координатных осях в поле ввода по оси ординат имена функций вводятся через запятую (при этом они будут располагаться друг под другом, а запятая на экране не отображается).
Mathcad допускает до 16 графиков в одной графической области.

Примеры построения графиков приведены на рис. 13.

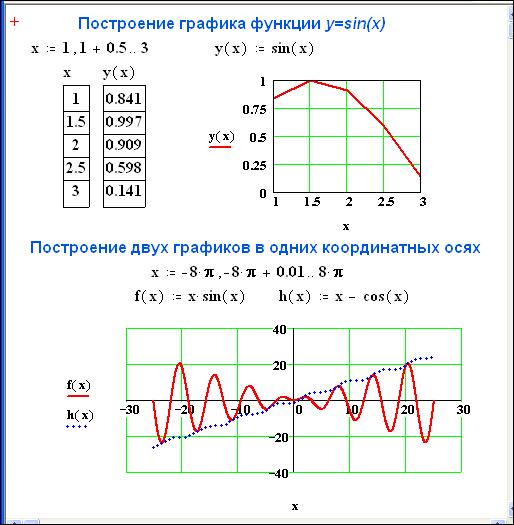
Рис. 13. Примеры построения графиков функций

Для изменения размера графика достаточно выделить его с помощью протягивания мыши (при этом область графика будет очерчена пунктирной рамкой) и растянуть его до желаемого размера.

Построенный график можно отформатировать: изменить тип, толщину и цвет линии, изобразить сетку, нанести риски на оси, сделать надписи и т. д. Диалоговое окно редактирования графика открывается двойным щелчком на графике и позволяет изменить доступные характеристики графика (рис. 14).

Аналогично электронным таблицам Excel система Mathcad обладает важным свойством автоматического пересчета результатов и изменения графиков в случае изменения исходных данных.

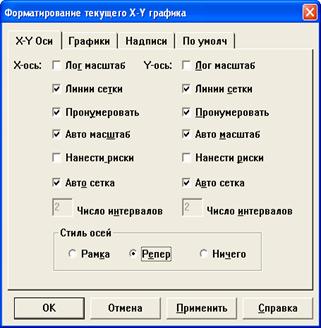
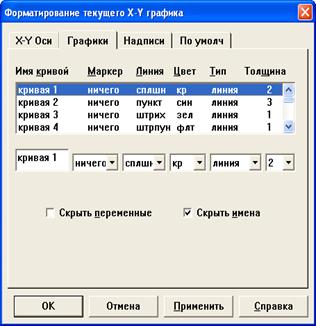
Рис. 14. Вкладки «Оси» и «Графики» диалогового окна форматирования графика

2.3. Лабораторная работа 2

Цель работы: изучение правил табуляции переменных, построения и форматирования графиков функций.

Задание. В соответствии с вариантом табл. 5 протабулировать функции и построить их графики сначала по отдельности, а затем в одной графической области. Вывести на экран таблицы значений дискретного аргумента и функций, в поле графиков изобразить линии сетки, для осей координат использовать стиль «репер». Текстовую часть работы оформить по образцу рис. 9, вычислительную и графическую – по образцу рис. 13.

Таблица 5

Исходные данные для табуляции функций и построения графиков

Вариант	Исходные данные	Диапазон и шаг изменения аргумента	Функции
	m = 4,4; с = 1,27	-2 ≤ t ≤ 2; D t = 0,25	,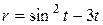
	y = 0,03	1 ≤ x ≤ 4; D x = 0,5	,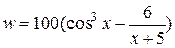
	b = 0,13	0 ≤ x ≤ 2; D x = 0,25	,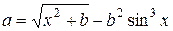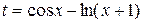
	b = 0,02; a = 1,1	0 ≤ x ≤ 1; D x = 0,1	,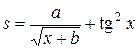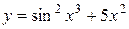
	b = 3,2	0 ≤ x ≤ 2,5; D x = 0,25	,
	b = 1,15; a = 1,7	2 ≤ x ≤ 4; D x = 0,25	,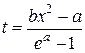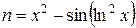
	b = –7,8; a = 2,25	0 ≤ t ≤ 2; D t = 0,1	,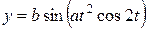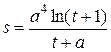
	b = 3,7; m = –0,5	0 ≤ t ≤ 2; D t = 0,1	,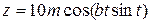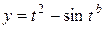
	b = 7,1; a = 1,5	1,3 ≤ x ≤ 2,5; D x = 0,1	,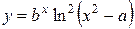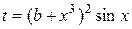
	a = 0,25	1 ≤ x ≤ 2; D x = 0,1	,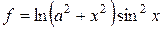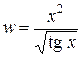
	a = 1,79	0 ≤ x ≤ 5; D x = 1	,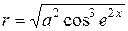
	m = 1,5	1,5 ≤ x ≤ 4; D x = 0,25	,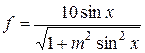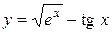
	a = –0,15	0 ≤ x ≤ 3; D x = 0,15	,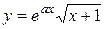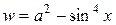
	m = 0,75	0,1 ≤ x ≤ 2,7; D x = 0,2	,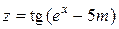
	a = 3,3	0 ≤ x ≤ 2; D x = 0,1	,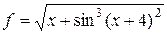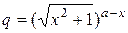
	a = 0,75 b = –7,1	0,1 ≤ x ≤ 2,7; D x = 0,2	,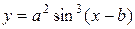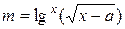

3. СИМВОЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ВЫЧИСЛЕНИЯ

3.1. Упрощение, интегрирование и дифференцирование выражений

При численных вычислениях результатом расчета является одно или несколько чисел. В символьной математике результатом вычисления выражения является другое выражение. Первоначальное выражение можно разложить на множители, упростить, проинтегрировать и т. д.

Для выполнения символьных вычислений рекомендуется исходное выражение заключить в уголковый курсор, ввести символьный знак равенства с помощью кнопки на палитре простых операторов , затем щелкнуть мышью вне выражения. Однако при этом не всегда удается достичь желаемого результата. Причиной этого является большая сложность и неоднозначность символьных задач, в связи с чем необходимо соблюдать ряд ограничений, накладываемых на использование символьного знака равенства.

Более надежным способом выполнения символьных преобразований является использование специальных команд для решения определенных задач из меню Символика. Рассмотрим их применение на конкретных примерах.

Пример 1. Упростить выражение (a² – b²)/(a + b).

Для решения этой задачи нужно набрать исходное выражение, заключить его в уголковый курсор, затем выполнить команду меню Символика → Упростить. Результат работы представлен на рис. 15.

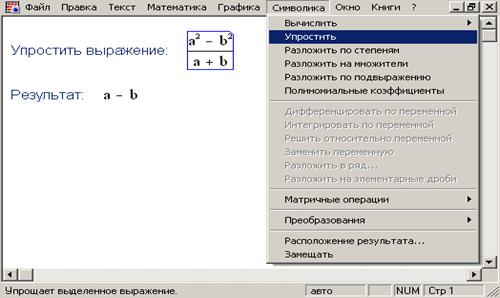
Рис. 15. Пример упрощения выражения

Команду Упростить можно применять не только для всего выражения целиком, но и для отдельной его части, помещенной в уголковый курсор.

Аналогично выполняются символьные команды разложения выражения по степеням, на множители, на элементарные дроби, вычисления пределов и др.

Пример 2. Проинтегрировать выражение x²∙e^x по переменной x.

Способ 1. Использование символьного оператора вычисления неопределенного интеграла:

1) с помощью кнопки палитры операторов математического анализа вводим в документ знак интеграла ;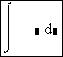

2) вводим подынтегральное выражение x²∙e^x в соответствующий слот;

3) вводим переменную интегрирования x после символа «d»;

4) заключаем все выражение в уголковый курсор и вводим знак символьного равенства с помощью кнопки : ;

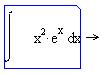5) выполняем щелчок вне области формулы, после чего Mathcad выводит результат символьного вычисления: .

Способ 2. Использование меню Символика:

1) набираем подынтегральное выражение;

2) устанавливаем курсор в любом месте выражения на переменной интегрирования x (при этом можно заключить переменную в уголковый курсор, а можно просто установить на нее курсор ввода данных);

3) выполняем команду Символика → Интегрировать по переменной.

Способ 3. Использование меню? → Шпаргалки → Математический анализ → Символьное интегрирование, где в окошко заготовки вводим подынтегральное выражение.

Пример 3. Продифференцировать выражение x²∙e^x по переменной x.

Способ 1. Использование символьного оператора производной .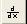

Способ 2. Использование меню Символика → Дифференцировать по переменной.

Способ 3. Использование меню? → Шпаргалки → Математический анализ → Символьное нахождение производной.

Все способы дифференцирования выполняются аналогично интегри-
рованию.

Для вычисления производных более высокого порядка можно применять оператор 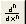(по способу 1), повторно дифференцировать выражение для производной низшего порядка (по способу 2), использовать специальную заготовку в Шпаргалках (по способу 3).

ВНИМАНИЕ! При выполнении символьных вычислений следует иметь в виду важное различие между символьным преобразованием, использующим меню Символика, и преобразованием с использованием символьного знака равенства. Результаты с правой стороны от символьного знака равенства вычисляются заново каждый раз при внесении изменений в рабочий документ. Результат, полученный с использованием меню Символика, модифицироваться не будет (при изменении исходных данных все такие преобразования нужно выполнить заново).

3.2. Лабораторная работа 3

Цель работы: изучение различных способов выполнения символьных вычислений.

Задание 1. Упростить выражение, заданное в графе 2 табл. 6.

Задание 2. Тремя способами найти первообразную, первую и вторую производную для функции, приведенной в графе 3 табл. 6. Текстовую часть работы оформить по образцу рис. 9 с использованием материала Шпаргалок.

Таблица 6

Исходные данные для символьных вычислений

Вариант	Выражение для упрощения	Выражение для вычисления первообразной и производных
1 1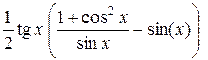

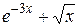
Продолжение табл. 6

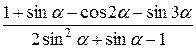
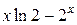
3 2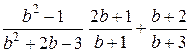

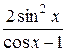
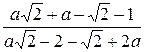
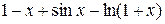
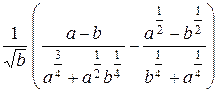
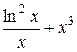
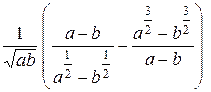
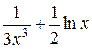
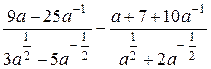
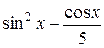
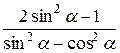
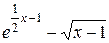
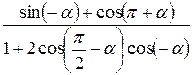
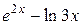
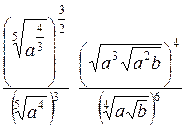
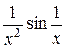
Окончание табл. 6

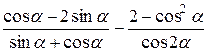
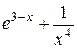
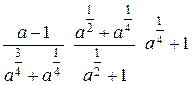
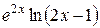
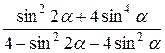
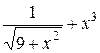
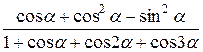
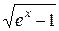
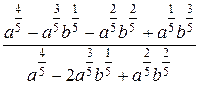
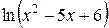
Библиографический список

1. MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95: Пер. с англ. М.: Филинъ, 1996. 712 с.

2. Информатика. Базовый курс. 2-е изд. / Под ред. С. В. Симоновича. СПб: Питер, 2005. 640 с.

Учебное издание

СИДОРОВА Елена Анатольевна,

СТУПАКОВ Сергей Анатольевич

ОСНОВЫ РАБОТЫ

В АВТОМАТИЗИРОВАННОЙ СИСТЕМЕ MATHCAD

________________________

Редактор Н. А. Майорова

***

Подписано в печать 02.10.2006. Формат 60 ´ 84 ¹/₁₆.

Плоская печать. Бумага офсетная. Усл. печ. л. 2,2. Уч.-изд. л. 2,4.

Тираж 500 экз. Заказ.

**

Редакционно-издательский отдел ОмГУПСа

Типография ОмГУПСа

*

644046, г. Омск, пр. Маркса, 35

Дата добавления: 2014-10-15