Додаток 1. Ціна і дохідність облігації з нульовим купоном

Ціна і дохідність облігації з нульовим купоном

Визначення дохідності облігації

11. Визначте дохідність облігації на час її погашення. Номінал облігації — 1000 дол., купонна ставка — 12 %, термін — 6 років. Поточна ціна облігації на час її погашення може бути: а) 920 дол.; б) 1020 дол.

12. Облігація номіналом 1000 дол., випущена на 10 років, була погашена, Інвестор отримав 9 % доходу на час погашення облігації, ціна облігації на час погашення становила 860 дол. Визнчте купонну ставку.

13. Облігація номіналом 1000 дол. випущена на термін 6 років із купонною ставкою 8 %. Утримувач облігації щорічно реінвестував отриманий купонний дохід перші три роки за ставкою 9 %, у наступні роки — за ставкою 7 %. Обчисліть повний реалізований дохід облігації.

14. Корпорація емітувала облігації номіналом 1000 дол., терміном на п”ять років із плаваючим купоном. Коливання купонної ставки прив’язано до руху ставки на федеральні облігації з тим самим терміном плюс 1 %. За п”ять років ставки коливалися від 4 % до 5 %. Підрахуйте купонний відсоток, припустивши, що ставки за федеральними облігаціями зростали за п’ять років рівномірно і визначте ціну облігації.

15. Визначте показник Макоулі, чутливість ціни облігації до зміни ринкових процентних ставок за облігацією номіналом 1000 дол., терміном на п’ять років, із купонною ставкою 12 %, очікувана дохідність — 10 %.

16. Облігація з нульовим купоном номіналом у 10000 дол. терміном на два роки продана за ціною 8573 дол. Розрахуйте дисконтну ставку.

17. Облігація з нульовим купоном номіналом 10000 дол. випущена на термін два роки, дисконтна ставка — 8 %. Визначте ціну облігації.

Число е [63]. У вищій математиці важливе значення має особливе число, що позначається символом е. Це число можна визначити як межу послідовності { a_n }, n -й член якої визначається за формулою:

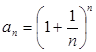, (1)

тобто

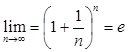. (2)

Число е є ірраціональним числом. Можна скласти таку таблицю (значення якої округляються до 0,001):

n						…
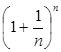
		2,594	2,704	2,717	2,718	…

Доведемо, що послідовність (1) збіжна. Для цього доведемо, що ця послідовність (див. § 4):

1) обмежена;

2) зростаюча.

На основі формули бінома Ньютона дістаємо:

,

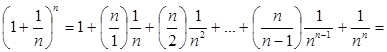
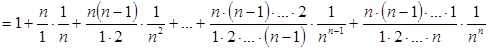або

.

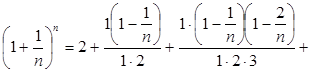
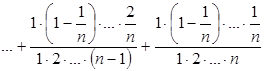Чисельник кожного дробу менший за одиницю, тому що він є добутком чисел, менших 1. Отже,

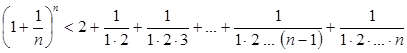. (3)

Зауважимо, що

1 × 2 = 2¹

1 × 2 × 3 > 1 × 2 × 2 = 2²

1 × 2 × 3 × 4 > 1 × 2 × 2 ×2 = 2³

............

1 × 2 × 3 ×... × n > 1 × 2 × 2 ×... × 2 = 2 ^{n – 1}

Якщо знаменники дробів замінити меншими, ніж вони, числами 2²,..., 2 ^{n – 1}, то

.

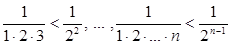З нерівності (3) маємо:

.

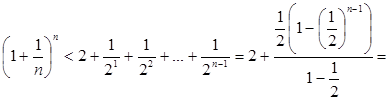
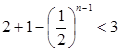Отже, ми довели, що послідовність обмежена.

Щоб довести, що послідовність буде зростаючою, достатньо довести, що a_n < a_{n + 1}. Маємо:

,

.

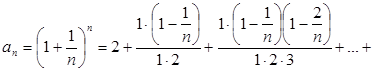
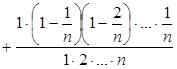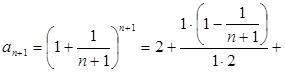
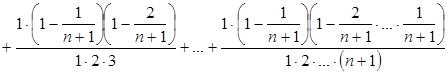Зауважимо, що

, .

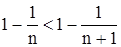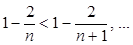Унаслідок цього

,

,

.....................

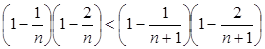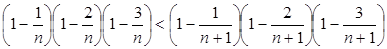Кожний член a_{n + 1} у наведеному розкладенні (починаючи з другого члена) більший, ніж відповідний член a_n; крім того, у розкладенні до a_{n + 1} на одного члена більше. Звідси a_n < a_{n + 1}.

Отже, ми довели, що послідовність { a_n } обмежена і зростаюча; тому (див. § 4) вона має межу.

Число е, розраховане до п’ятого десяткового знака, є е = 2,71828.

Дата добавления: 2014-11-06