Решение. Учебное пособие по курсу аналитической геометрии

Учебное пособие по курсу аналитической геометрии

«Решение типовых задач»

Составил: Влайков Н.Д.

Рецензент: к.ф.-м.н. Савотин А.И.

г. Калуга, 2011 г.

Содержание.

1. Уравнение прямой и плоскости в пространстве стр. 2

2. Уравнения кривых второго порядка стр.7

3. Матричные уравнения стр. 8

4. Решение СЛАУ стр. 10

5. Задачи для самостоятельного решения стр. 14

6. Список рекомендуемой литературы стр. 16

1. Уравнение плоскости и прямой в пространстве.

Даны координаты четырех точек в пространстве .

Найти:

1. Уравнение плоскости, проходящей через точки .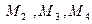

2. Уравнение и длину перпендикуляра, опущенного из т. на плоскость, проходящую через точки .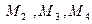

3. Расстояние от т. 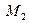до прямой, проходящей через точки .

4. Точку, симметричную точке 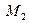, относительно прямой, проходящей через точки .

5. Выполнить чертеж.

1.1. Уравнение плоскости, проходящей через три заданные точки , , 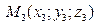имеет вид:

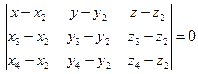. Для наших точек: . Вычислим определитель: следовательно, уравнение искомой плоскости .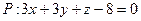

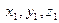1.2. Составим уравнение перпендикуляра, опущенного из т. на плоскость, проходящую через точки . Запишем это уравнение в каноническом виде: , где - координаты точки, принадлежащей прямой, а в знаменателях записаны соответствующие координаты направляющего вектора . Координаты точки , принадлежащей прямой, нам известны. В качестве направляющего вектора, возьмем нормальный вектор плоскости. Т.е. .

Запишем уравнение перпендикуляра: .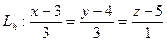

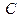Длина перпендикуляра может быть найдена как расстояние от т. до плоскости по формуле: , где , , - координаты нормального вектора плоскости, а 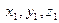- координаты точки .

.

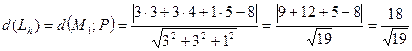1.3. Расстояние от т. 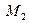до прямой, проходящей через точки .

а) Общий вид уравнения прямой проходящей через две заданные точки 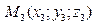, 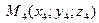имеет вид: 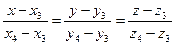. Для наших точек:

; ;

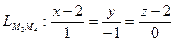б) Теперь найдем расстояние от точки 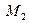до прямой 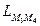. Для этого составим уравнение плоскости 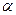, проходящей через т. 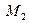, перпендикулярно прямой . Уравнение плоскости, проходящей через т. , с нормальным вектором 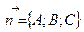имеет вид: .

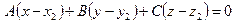Координаты т. 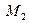известны, а в качестве нормального вектора можно выбрать направляющий вектор прямой : . Подставим координаты в уравнение: 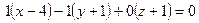; раскрыв скобки и приведя подобные слагаемые получим уравнение плоскости .

в) Найдем координаты точки 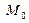- точки пересечения прямой и плоскости 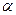. Точка - будет являться основанием перпендикуляра опущенного из т. 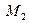на прямую . Т.к. т. принадлежит и прямой и плоскости, ее координаты должны удовлетворять двум уравнениям, следовательно, координаты можно найти, решив систему:

;

Для этого перейдем к параметрическому уравнению прямой :

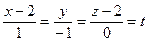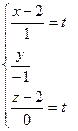; выразим 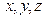через параметр : .

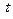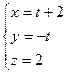Подставим в уравнение плоскости 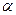и решим его: 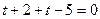; 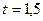. Найдем из системы: ; ; .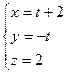

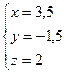Следовательно, координаты т. .

г) Расстояние от т. 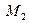до прямой, проходящей через точки можно найти как расстояние между точкам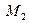и и 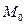по формуле: .

.

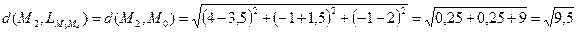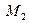1.4. Найдем координаты т. , симметричной точке , относительно прямой, проходящей через точки . Координаты точки можно найти из условия: т. 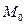- середина отрезка 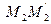(т.к. прямая 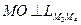). Координаты середины отрезка можно найти по формулам: 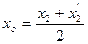, , 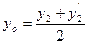. Следовательно, координаты т.

можно найти так: , , .

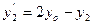Т.е. , , .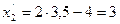

.

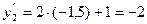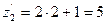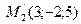1.5. Построим несколько поясняющих чертежей:

1.5.1. Построим точки . Для примера построим т.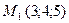

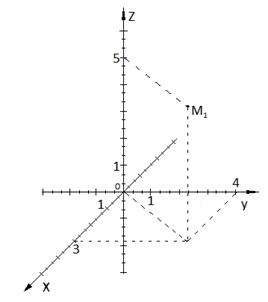
Рис 1.1 Точка

1.5.2. На рис 1.2 построим плоскость 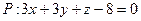, приведя общее уравнение к уравнению плоскости в отрезках: ; ;

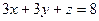Рис 1.2 плоскость .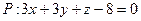

1.5.3. Изобразим прямую :

Рис 1.3 прямая

1.5.4. Построим точку :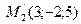

Рис 1.4 Точка .

1. Уравнения кривых второго порядка.

Определить тип каждого из уравнений, привести к каноническому виду; установить, какие геометрические образы они определяют и изобразить на чертеже. Найти координаты центра, полуоси, фокусы, эксцентриситет, уравнения асимптот и директрис.

Дано: уравнение второго порядка

.

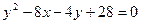Решение:

Сгруппируем слагаемые, содержащие 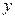и дополним до полного квадрата: ; ; 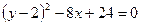; 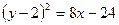вынесем за скобки коэффициент при : 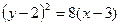. Т.о. привели уравнение к виду - каноническое уравнение параболы с вершиной в т. 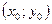и осью симметрии параллельной 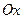. Следовательно, для нашего примера: уравнение определяет параболу. Вершина в т. . Параметр Ветви направлены вправо. Уравнение директрисы для несмещенной параболы 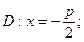для смещенной 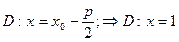. Фокус имеет координаты .

Построим график:

Дополнительные точки

	-2
			3,5	3,5

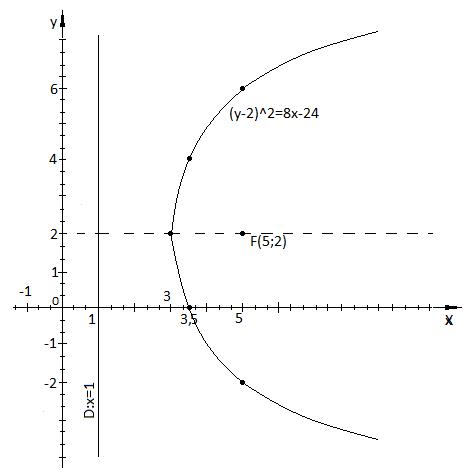
Рис.2.1 Парабола

1. Матричные уравнения.

Решить матричное уравнение: 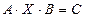, (3.1)

где

; ; .

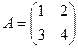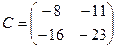Дата добавления: 2014-11-06