
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гидравлические потери
|
|
|
|
Разность давлений масла в двух сечениях одного и того же трубопровода при условии, что первое расположено выше по течению, а второе – ниже, определяется уравнением Бернулли:
 ,
,
где h2 – h1 – разность высот центров тяжести сечений от произвольно выбранного горизонтального уровня;
v1, v2 – cредние скорости масла в сечениях;
g – ускорение силы тяжести;
 – сумма гидравлических потерь при движении масла из первого сечения во второе.
– сумма гидравлических потерь при движении масла из первого сечения во второе.
Уравнение Бернулли в полном виде используется для расчета всасывающих линий насосов; в остальных случаях первым слагаемым, как правило, пренебрегают и считают:

Гидравлические потери обычно разделяют на местные потери и потери на трение по длине трубопровода (линейные).
1.5.1 Местные потери энергии обусловлены местными гидравлическими сопротивлениями, вызывающими деформацию потока. Местными сопротивлениями являются: сужения, расширения, закругления трубопроводов, фильтры, аппаратура управления и регулирования и пр. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри.
Потери давления от местных сопротивлений определяют по формуле Вейсбаха:
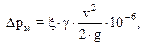 МПа (или
МПа (или  Па),
Па),
где 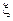 (кси) – коэффициент сопротивления или потерь,
(кси) – коэффициент сопротивления или потерь,
v – средняя по сечению скорость потока в трубе за местным сопротивлением, м/с;  , Н/м3; g=9,81 м/с2.
, Н/м3; g=9,81 м/с2.
Каждое местное сопротивление характеризуется своим значением коэффициента 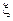 . При турбулентном течении значения
. При турбулентном течении значения 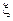 определяются, в основном, формой местных сопротивлений и очень мало изменяются с изменением размеров сечения, скорости потока и вязкости жидкости. Поэтому принимают, что они не зависят от числа Рейнольдса Re.
определяются, в основном, формой местных сопротивлений и очень мало изменяются с изменением размеров сечения, скорости потока и вязкости жидкости. Поэтому принимают, что они не зависят от числа Рейнольдса Re.
Значения 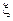 , например, для тройников с одинаковыми диаметрами каналов, принимают равными, если:
, например, для тройников с одинаковыми диаметрами каналов, принимают равными, если:
потоки складываются, расходятся; поток проходящий;
 =0,5-0,6
=0,5-0,6  =1,5-2
=1,5-2  =0,3
=0,3  =1-1,5
=1-1,5  =0,1
=0,1  =0,05
=0,05
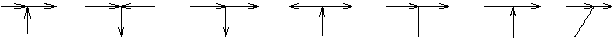
 =0,7
=0,7  =0,9-1,2
=0,9-1,2  =2
=2
при повороте трубопровода 
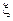 = 1,5-2 и т.д. [с. 390-391]
= 1,5-2 и т.д. [с. 390-391]
Значения  для конкретных сопротивлений, встречающихся в гидросистемах оборудования, берут из справочной литературы.
для конкретных сопротивлений, встречающихся в гидросистемах оборудования, берут из справочной литературы.
При ламинарном режиме (Re<2200) потери давления зависят, в основном, от гидравлического трения в местных сопротивлениях, а значит, при их определении надо учитывать величину Re.
Потери давления от местных сопротивлений при ламинарном режиме определяются по формуле:
 МПа,
МПа,
где 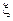 л = а×
л = а× 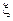 и поправочный коэффициент ламинарности
и поправочный коэффициент ламинарности 
Величины потерь давления в стандартных гидравлических устройствах для номинального расхода жидкости обычно приводятся в их технических характеристиках.
1.5.2 Потери на трение по длине - это потери энергии, которые возникают в прямых трубах постоянного сечения, т.е. при равномерном течении жидкости, и возрастают пропорционально длине трубы. Эти потери обусловлены внутренним трением в жидкости, а поэтому имеют место и в шероховатых, и в гладких трубах.
Потери давления на трение в трубопроводе определяется по формуле Дарси:
 МПа,
МПа,
где 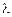 – коэффициент трения в трубопроводе;
– коэффициент трения в трубопроводе;
l и d – длина и внутренний диаметр трубопровода, мм.
Эта формула применима как при ламинарном, так и при турбулентном течении; различие заключается лишь в значениях коэффициента  .
.
При ламинарном режиме (Re<2200) коэффициент трения является функцией основного критерия напорных потоков - числа Рейнольдса и рассчитывается по формуле:
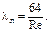
При турбулентном течении коэффициент трения является не только функцией числа Re, но зависит и от шероховатости внутренней поверхности трубы. Для гидравлически гладкой трубы, т.е. с такой шероховатостью, которая практически не влияет на ее сопротивление, коэффициент трения при турбулентном режиме можно определить по формуле П.К. Конакова:

Трубу считают гидравлически гладкой, если (d/k)>(Re/20), где k – эквивалентная шероховатость, мм. Например, для новых бесшовных стальных труб k≈0,03 мм, а после нескольких лет эксплуатации k≈0,2 мм, для новых цельнотянутых труб из цветных металлов k≈0,005 мм. Такие трубы часто используются в гидросистемах металлорежущих станков.
Коэффициент трения при турбулентном режиме можно определить по формуле Альтшуля, являющейся универсальной (т.е. применимой в любых случаях):
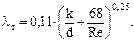
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 1293; Нарушение авторских прав?; Мы поможем в написании вашей работы!