Вводная часть. Основная цель данной работы состоит в изучении принципов получения заданного цвета на экране цветного телевизора

Основная цель данной работы состоит в изучении принципов получения заданного цвета на экране цветного телевизора. Принятый в настоящее время способ формирования заданного цвета базируется на трёхкомпонентной теории цветового зрения, а все математические соотношения, необходимые для технической реализации способа, могут быть получены из колориметрии.

Классификация и стандартизация цветов производятся с помощью колориметрической системы X Y Z. Для того чтобы получить на экране телевизора некоторый цвет, заданный координатами x′, y′, z′ в системе X Y Z, необходимо знать свойства воспроизводящего приёмного устройства. Так как люминофоры трёхцветных кинескопов в настоящее время стандартизированы, целесообразно ввести колориметрическую систему первичных (основных) цветов приёмника R G B, которая на языке колориметрии описывает свойства воспроизводящего устройства. Однозначная связь между колориметрическими системами X Y Z и R G B позволяет по заданным координатам x′, y′, z′ некоторого цвета найти координаты r′, g′, b′ того же цвета в системе R G B.

Для того, чтобы воспроизвести этот цвет на экране телевизора, необходимо сформировать сигналы цветоделенных изображений U_R, U_G, U_B, пропорциональные координатам цвета r′, g′, b′, т.е.

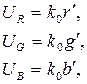(1)

и подать эти сигналы на модуляторы «красного», «зелёного» и «синего» прожекторов трёхцветного кинескопа.

Напомним также, что возможен и другой равнозначный способ воспроизведения этого цвета на экране цветного телевизора, при котором из сигналов цветоделенных изображений U_R, U_G, U_B формируется яркостный сигнал Е_Y и три цветоразностных сигнала E_R-Y, E_G-Y, E_B-Y. При опорном белом (равносигнальном) цвете С (Х= 0,31; Y = 0,316) выражения для этих сигналов имеют вид:

(2)

Из выражений (1) и (2) следует, что для формирования сигналов, управляющих работой трёхцветного кинескопа, достаточно знать координаты r′, g′, b′ цвета, который необходимо воспроизвести на экране телевизора. Входящий в формулу (1) коэффициент пропорциональности k₀ может иметь любое значение, и от этой величины зависит яркость воспроизводимого цветного изображения. В системе цветного телевидения сигналы цветоделенных изображений U_R, U_G, U_B, пропорциональные координатам r′, g′, b′, вырабатываются передающими камерами, а при настройке приёмника изменением величины k₀ достигается требуемая яркость изображения на экране цветного кинескопа.

В данной работе исследуется устройство, формирующее искусственные сигналы U_R, U_G, U_B, с помощью которых на экране телевизора воспроизводится изображение в виде вертикальных цветных полос. Цветность свечения той или иной полосы определяется соотношением амплитуд сигналов U_R, U_G, U_B, а яркость может изменяться от минимальной до максимальной одновременной регулировкой размаха этих сигналов при соблюдении прежнего соотношения между ними (т.е. при неизменной цветности).

В процессе выполнения лабораторной работы необходимо провести расчёт координат r′, g′, b′ цвета, заданного в колориметрической системе X Y Z. Задание выдаётся преподавателем указанием положения точки в треугольнике основных цветов на цветовом графике МКО в координатной системе XYZ (см. рисунок 1). Это соответствует заданию единичного цвета, для которого по цветовому графику можно определить трёхцветные коэффициенты x y z. Напомним, что трёхцветные коэффициенты x y z являются частными значениями координат x′, y′, z′, при которых их сумма равна 1. Это позволяет в данном случае использовать для вычисления координат r′, g′, b′ матричное уравнение

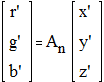
(3)

Цвета расположенные за пределами треугольника не могут быть отображены ни какими средствами телевидения и полиграфии.

1 – Зелёный; 2 – Морская волна; 3 – Жёлто-зелёный; 4 – Жёлтый; 5 – Оливковый; 6 – Хаки; 7 – Жёлто-оранжевый; 8 – Охра; 9 – Бежевый; 10 – Оранжевый; 11 – Светло-оранжевый; 12 – Киноварь; 13 – Розовый; 14 – Красный; 15 – Кармин; 16 – Область белого; 17 – Гранатовый; 18 – Пурпурный; 19 – Сиреневый; 20 – Фиолетовый; 21 – Индиго; 22 – Тёмно-синий; 23 – Синий; 24 – Сапфировый; 25 – Небесно-голубой; 26 – Изумрудный.

Рисунок 1 – Треугольник основных цветов на цветовом графике МКО в координатной системе XYZ

в которое вместо x′, y′, z′ следует подставлять найденные по цветовому графику значения трёхцветных коэффициентов x y z. Здесь А_n - квадратная матрица, элементами которой являются координаты цветов X Y Z в колориметрической системе R G B. При опорном белом цвете С матрица А_n имеет вид:

После того, как рассчитаны величины r′, g′, b′, можно определить сигналы U_R, U_G, U_B, которые необходимо подать на трёхцветный кинескоп для получения заданного цвета свечения экрана.

Примечание. Получив задание, необходимо проверить, находится ли заданный цвет внутри треугольника R G B. В противном случае получить заданный цвет на экране телевизора не представляется возможным.

Дата добавления: 2014-11-06