Прогнозная цена 1 погонного Прогнозная цена 1 килограмма

метра прутка стали 40Х

0,8 0,9

120 140 руб. 80 90 110 руб.

Прогнозная цена 1 килограмма Прогнозная цена 1 килограмма

пластмассы латуни

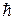
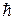
0,7 0,6

0,4

15 20 30 40 руб. 150 200 руб.

Рис. 2.3. Прогнозные значения цен на материалы.

Решение:

Обозначим нечеткие числа, описывающие прогнозные цены на материалы следующим образом: 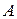– цена стали; 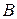– латуни; – прутка; – пластмассы. Тогда:

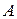=(90;90;10;20;0,9); 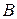=(150;150;0;0;0,6) (200;200;0;0;0,4); =(120;140;0;0;0,8); =(20;30;5;10;0,7).

Затраты на материалы с учётом их норм расхода:

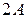=(180;180;20;40;0,9); =(225;225;0;0;0,6) (300;300;0;0;0,4);

=(60;70;0;0;0,8); =(60;90;15;30;0,7).

Прогнозная сумма материальных затрат будет представлена нечётким числом:

.

Вычислим :

;

; ;

;

.

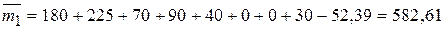Таким образом, .

Аналогично вычислим :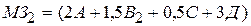

;

;

;

;

;

.

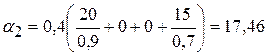Для прогнозной суммы затрат получаем следующее выражение:

Функция принадлежности числа 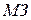представлена на рис. 2.4.

0,6

0,4

490 516,19 582,61 675,08 710 руб.

Рис. 2.4. Функция принадлежности прогнозного значения

суммы затрат на материалы.

Тема 3. Методы экстраполяции (аппроксимация динамического ряда аналитическими функциями)

Экстраполяция (распространение прошлых и настоящих закономерностей на будущее) является наиболее распространённым методом краткосрочного прогнозирования экономических явлений.

При использовании методов экстраполяции исходят из предположения, что динамика развития объекта прогнозирования, отмеченная за последние годы, сохранится также и на ближайшую перспективу.

Наиболее информативным, но и более трудоёмким методом экстраполяции является аппроксимация динамического ряда аналитическими функциями. При аппроксимации динамического ряда аналитическими функциями предполагается, что для прогнозирования будет использована функция, адекватно описывающая динамику развития объекта прогнозирования. Чаще всего для аппроксимации используются:

- линейная функция ;

- парабола ;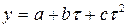

- гипербола ;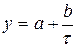

- логарифмическая функция ;

- экспоненциальная функция .

Каждая функция имеет свою сферу применения. Например, линейная функция используется для описания равномерно развивающихся процессов, а гипербола хорошо описывает процессы, для которых характерно насыщение рынка.

Для определения значений эмпирических коэффициентов 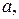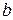и 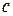обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:

,

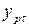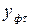где и - расчётные и фактические значения;

- число наблюдений.

Так для линейной функции имеем:

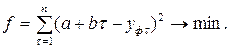
Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдём неизвестные эмпирические коэффициенты:

или

При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:

,

где - коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 3.1);

- среднее квадратическое отклонение от тренда:

.

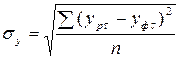Таблица 3.1

Значения коэффициента доверия по распределению Стьюдента

Уровень доверительной вероятности,	0,683	0,95	0,99	0,997
Коэффициент доверия,		1,96	2,576

Пример. Данные об объеме реализации автомобилей фирмой «Шумахер» за пять лет приведены в таблице 3.2.

Таблица 3.2

Объём продаж автомобилей фирмой «Шумахер»

Порядковый номер
Год
Количество проданных автомобилей, шт.

Необходимо составить прогноз объёмов продаж на 2006 год, используя линейную и параболическую функции.

Решение:

Результаты предварительных расчётов сведём в таблицу 3.3.

Таблица 3.3

Дата добавления: 2014-11-06