Тема 4. Экономико-статистическое моделирование

Расчет эмпирических коэффициентов

Срок, лет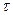
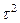
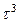
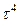
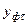
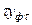
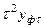
до 15					28,26	28,26	28,26
15-19					60,56	121,12	242,24
20-24					94,9	284,7	854,1
25-29					136,1	544,4	2177,6
30-34					183,7	918,5	4592,5
Старше 35					242,25	1453,5
Сумма					745,77	3350,48	16615,7

Система уравнений, решая которую определим эмпирические коэффициенты параболической функции, имеет вид:

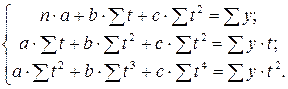
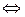
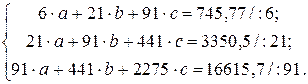
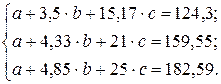
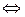
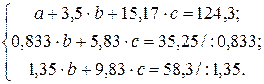
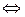
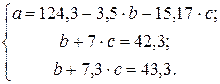
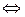
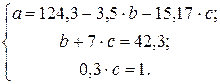
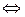
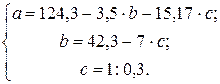
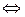
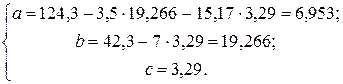
Таким образом, зависимость общих потерь от срока службы сетей имеет следующий вид:

.

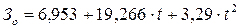Рациональный срок службы трубопровода определим из уравнения:

.

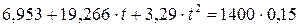Решая данное уравнение, получаем: .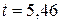

Учитывая, что интервал между периодами составляет 5 лет, получим величину рационального срока службы: 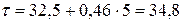лет (32,5 – середина интервала срока службы 30-34).

Таким образом, целесообразно заменить 31,6 км водопроводных сетей.

Экономико-статистические модели представляют собой вид моделей, описывающих с помощью уравнений регрессии зависимости между влияющими факторами и результирующим фактором. Различают однофакторные и многофакторные модели. Многофакторные модели позволяют изучать влияние на объект прогнозирования нескольких факторов, однофакторные – одного. На практике наибольшее применение нашли экономико-статистические модели линейного вида:

,

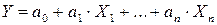где 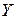- результирующий фактор;

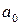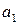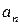, , … - эмпирические коэффициенты;

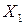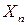, … - влияющие факторы.

Для определения значений эмпирических коэффициентов обычно используется метод наименьших квадратов (см. тему 3). Рассмотрим процедуру разработки многофакторной экономико-статистической модели на следующем примере.

Пример. Необходимо построить экономико-статистическую модель зависимости объёма выпускаемой продукции на предприятиях, работающих в одной отрасли, от составляющих ресурсного потенциала: численности работников, оборотных и основных средств. Исходные данные приведены в таблице 4.1.

Таблица 4.1

Значения показателей

Наименование предприятия	Численность работников, чел.	Основные средства, млн. руб.	Оборотные средства, млн.руб.	Объём выпускаемой продукции, млн.руб
ООО «Конструктор»
ООО «Заря»
ООО «Механик»
ООО «Инженер»
ООО «Инноватор»
ООО «Исследователь»

Решение:

При построении экономико-статистической модели будем исходить из предположения, что зависимость между результирующим фактором (объёмом выпускаемой продукции - 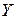) и влияющими факторами (численность работников - 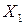, основные средства - 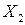, оборотные средства - 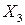) имеет линейный вид:

.

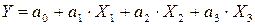Система уравнений, в результате решения которой будут определены эмпирические коэффициенты, будет следующей:

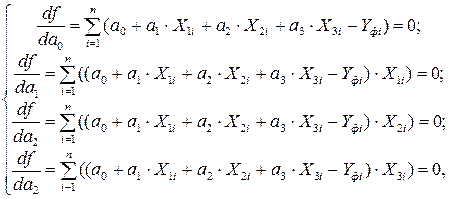
или

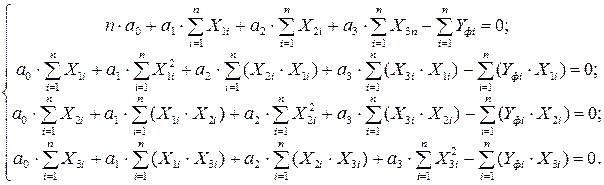
Промежуточные расчёты эмпирических коэффициентов сведем в таблицу 4.2.

Таблица 4.2а

Промежуточные расчёты коэффициентов

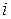
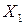
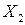
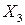
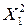
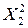
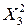
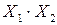
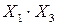
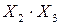
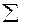
Таблица 4.2б

Промежуточные расчёты коэффициентов

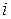
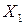
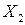
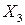
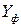
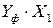
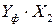
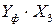
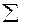
После подстановки результатов промежуточных расчётов в систему уравнений, имеем:

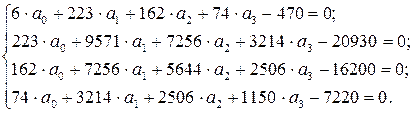
Можно решать данную систему уравнений так, как это было показано в предыдущем параграфе. А можно воспользоваться программным продуктом EXCEL.

Вариант 1. Запишем данную систему в матричном виде:

.

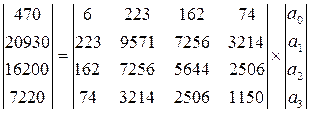Тогда вектор-столбец эмпирических коэффициентов равен:

.

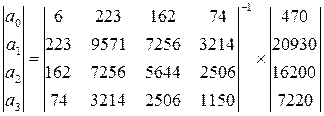Для расчёта обратной матрицы занесем исходную матрицу в ячейки (рисунок 4.1).

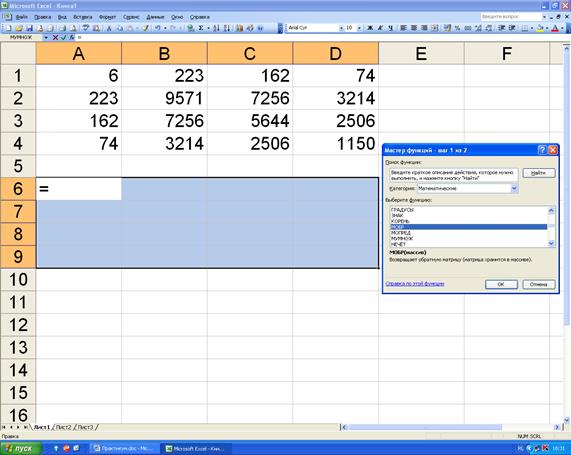
Рисунок 4.1. Вызов функции расчёта обратной матрицы.

Выделим ячейки, в которые будут помещены коэффициенты обратной матрицы (так как размерность матрицы в нашем случае 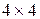, то выделяем массив 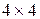- A6:D9). Функция «определить матрицу обратную данной» относится к категории «математические функции». Нажмём кнопку и далее категорию «математические функции» и выберем функцию «МОБР» - расчёт обратной матрицы

Диалоговое окно функции «МОБР» приведено на рисунке 4.2. В строке «Массив» укажем массив ячеек, содержащих элементы исходной матрицы. После того как информация будет занесена, необходимо нажать на клавиатуре одновременно клавиши «Ctrl», «Shift» и «Enter». Результат расчёта обратной матрицы представлен на рисунке 4.3.

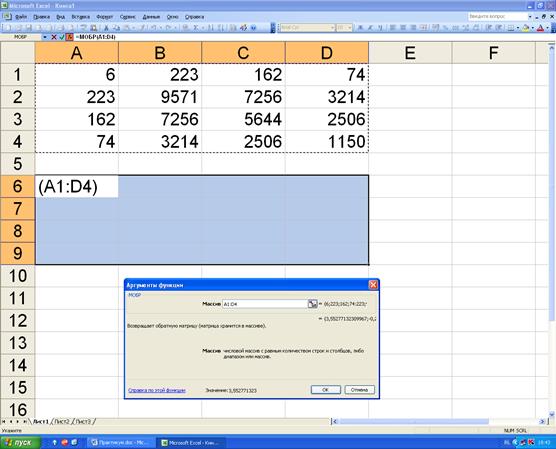
Рисунок 4.2. Диалоговое окно функции «МОБР».

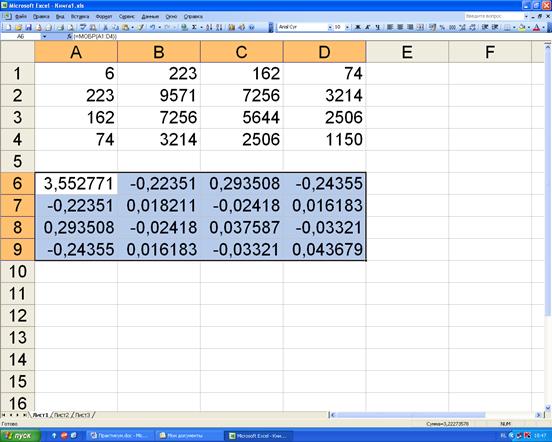
Рисунок 4.3. Результат расчёта обратной матрицы.

Коэффициенты модели определим перемножив обратную матрицу на вектор-столбец значений результирующего фактора:

.

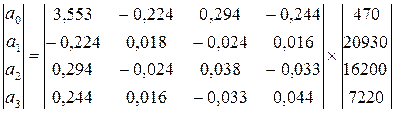Выделим столбец ячеек (4 ячейки), в которые будут помещены значения коэффициентов. Откроем диалоговое окно функции «МУМНОЖ» в категории математических функций (рисунок 4.4). В массив 1 занесём адреса ячеек, содержащих значения коэффициентов обратной матрицы (А6:D9). В массив 2 - адреса ячеек, содержащих значения результирующего фактора.

Далее одновременно нажимаем клавиши «Ctrl», «Shift» и «Enter». На рисунке 4.5 представлен результат расчёта коэффициентов модели.

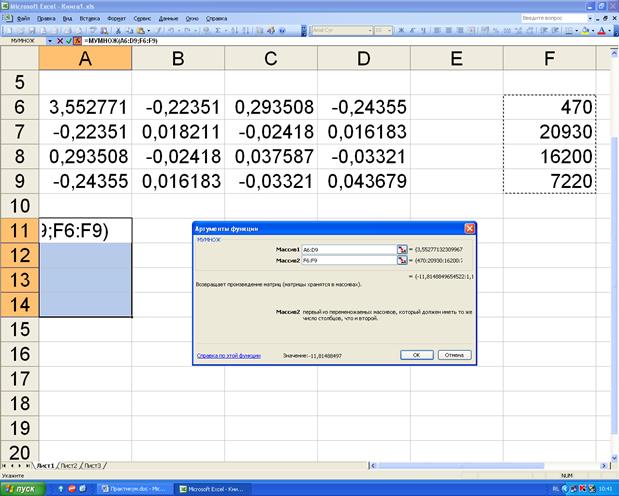
Рисунок 4.4. Диалоговое окно функции «МУМНОЖ».

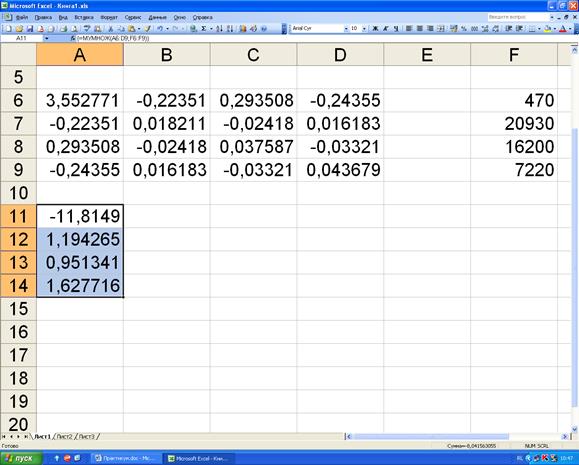
Рисунок 4.5. Результат расчёта коэффициентов модели.

Таким образом, экономико-статистическая модель зависимости объёма выпускаемой продукции от влияющих факторов будет следующей:

.

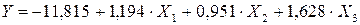Вариант 2. Занесём исходные данные в ячейки. В диалоговом окне кликнем опцию «сервис - надстройки» и установим пакет анализа (рис. 4.6). После установки «Пакета анализа» снова кликнем опцию «сервис» и выберем операцию «анализ данных». В диалоговом окне операции «анализ данных» выберем инструмент анализа «регрессия».

На рисунке 4.7 показано диалоговое окно инструмента анализа «регрессия». В строке «Входной интервал Y» укажем адреса ячеек, содержащих значения результирующего фактора - $E$3:$E$8. В строке «Входной интервал Х» укажем адреса ячеек, содержащих значения влияющих факторов - $B$3:$D$8. В строке «Выходной интервал» укажем адреса ячеек, в которые будут внесены результаты расчётов.

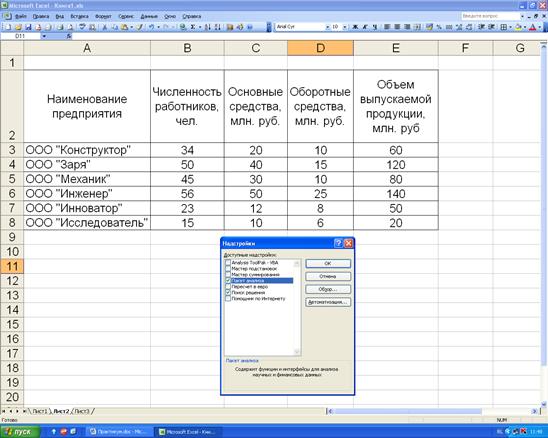
Рисунок 4.6. Установка Пакета анализа.

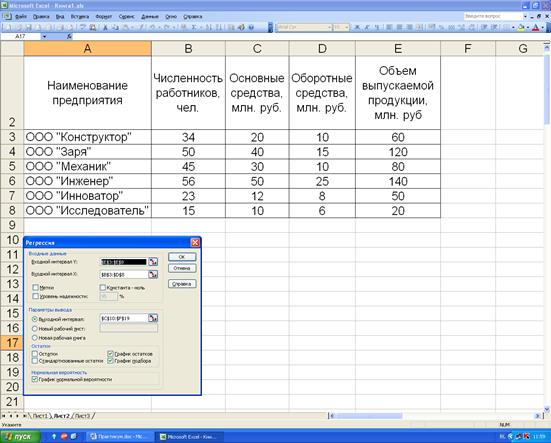
Рисунок 4.7. Диалоговое окно инструмента анализа – «регрессия».

Далее одновременно нажимаем клавиши «Ctrl», «Shift» и «Enter». На рисунке 4.8 представлен результат расчёта коэффициентов модели. Значения коэффициентов содержатся в ячейках I27-I30.

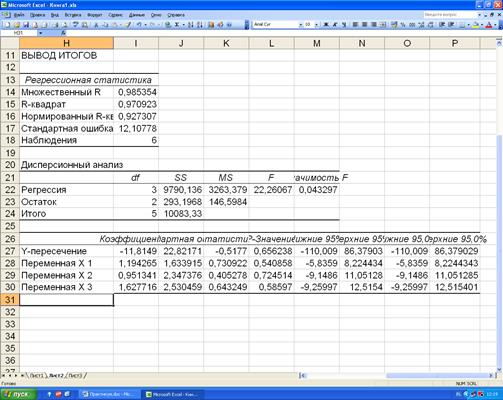
Рисунок 4.8. Результат расчёта коэффициентов модели в Пакете анализа.

Достоинством «Пакета анализа» является то, что он позволяет также получить качественную оценку полученной экономико-статистической модели.

После построения экономико-статистической модели определим отклонения теоретических значений от фактических, для чего подставим значения влияющих факторов 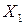, , 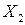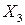в экономико-статистическую модель. Например, для ООО «Конструктор» теоретическое значение результирующего фактора составит:

.

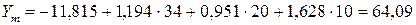Отклонение теоретического значения результирующего фактора от фактического:

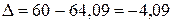
Результаты расчётов сведем в таблицу 4.3.

Таблица 4.3

Результаты расчётов по экономико-статистической модели

Наименование предприятия	Теоретическое значение,	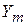Фактическое значение,	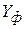Отклонение,
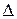
ООО «Конструктор»	64,09		-4,09
ООО «Заря»	110,37		9,63
ООО «Механик»	86,74		-6,74
ООО «Инженер»	143,32		-3,32
ООО «Инноватор»	40,09		9,9
ООО «Исследователь»	25,38		-5,38

Анализируя данные, представленные в таблице 4.3, следует отметить, что с одной стороны отклонение теоретических значений результирующего фактора от фактических значений может носить случайный характер. С другой стороны вполне возможно, что предприятия ООО «Конструктор», ООО «Механик», ООО «Инженер», ООО «Исследователь» используют свой потенциал недостаточно эффективно.

Вывод о недостаточной эффективности использования ресурсного потенциала следует из следующих рассуждений. Теоретические значения результирующего фактора показывают величины объёмов выпускаемой продукции предприятиями при одинаковой средневзвешенной эффективности использования производственных ресурсов. Отклонения 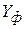от 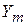в меньшую сторону свидетельствуют об использовании ресурсов с меньшей степенью эффективности. И наоборот, превышение 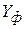над 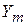свидетельствует о том, что предприятия используют ресурсы более эффективно.

Дата добавления: 2014-11-06