Информационная модель межотраслевого баланса в натуральном выражении

Определить индексы роста цен в отраслях, если известно, что объёмы материального производства остались на прежнем уровне, заработная плата во второй отрасли выросла в 1,5 раза, а в первой осталась неизменной.

Решение:

Обозначим индексы роста цен в первой и второй отрасл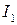и и 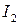, тогда, после повышения заработной платы во второй отрасли, уравнения запишутся следующим образом:

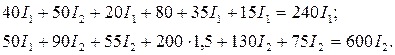
После преобразований получим:

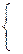
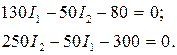
Решая данную систему уравнений, находим индексы роста цен:

, .

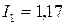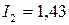Стоимостной баланс экономики после повышения заработной платы во второй отрасли в 1,5 раза представлен в таблице 7.4.

Таблица 7.4

Стоимостной баланс экономики после повышения заработной платы во второй отрасли в 1,5 раза, млрд.руб.

Отрасли производители	Отрасли потребители	Конечный продукт	Валовый выпуск
	46,8	58,5	174,8	280,1
	71,5	128,7	658,7	858,9
Амортизация	23,4	78,8
Заработная плата
Прибыль	40,9	185,9
Налоги	17,5	107,2
Валовые затраты	280,1	858,9

Сегодня одним из инструментов государственного регулирования инфляции является фиксация цен на ресурсы, производимые той или иной отраслью. Например, фиксация цен на образовательные услуги в государственных вузах. При этом цены на ресурсы, производимые другими отраслями, не фиксируются. Используя балансовый метод планирования можно просчитать, насколько изменится добавленная стоимость по отраслям.

Пример. Стоимостной баланс экономики, состоящий их двух отраслей представлен в таблице 7.5.

Таблица 7.5

Стоимостной баланс экономики, млрд. руб.

Отрасли производители	Отрасли потребители	Конечный продукт	Валовый выпуск
Добавленная стоимость
Валовые затраты

Определите, как изменится добавленная стоимость по отраслям, если цены на ресурсы первой отрасли вырастут в 1,2 раза, а цены на ресурсы второй отрасли останутся фиксированными.

Решение:

Обозначим индексы изменения величины добавленной стоимости в первой и второй отрасл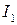и и 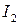, тогда, уравнения запишутся следующим образом:

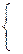
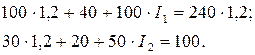
После преобразований получим:

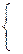
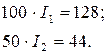
Таким образом, индекс роста добавленной стоимости в первой отрасли составит 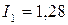, а во второй 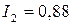. Сравнивая заработную плату работников первой и второй отраслей, можно ожидать, что заработная плата работников первой отрасли по сравнению с заработной платой работников второй отрасли увеличится в 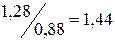раза.

Стоимостной баланс экономики представлен в таблице 7.6.

Таблица 7.6

Стоимостной баланс экономики после фиксации цен на ресурсы второй отрасли и росте цен в 1,2 раза на ресурсы первой отрасли, млрд.руб.

Отрасли производители	Отрасли потребители	Конечный продукт	Валовый выпуск
Добавленная стоимость
Валовые затраты

На сегодняшний день перспективным средством мотивации работников организации является вовлечение персонала в процессы принятия решений. Эта задача решается путём реализации принципа управления по центрам ответственности, когда каждое подразделение организации имеет свой бюджет, который формируется и зависит от результатов деятельности. При этом, коллектив (руководитель) структурного подразделения имеет возможность распоряжаться бюджетом, но обязан, в свою очередь, полностью выполнять плановые задания. Инструментом, позволяющим сформировать сбалансированные бюджеты подразделений, является балансовый метод.

Пример. Стоимостной баланс при изготовлении изделия А структурными подразделениями предприятия представлен в таблице 7.7.

Таблица 7.7

Стоимостной баланс изготовления детали А, руб.

Подразделения производители	Подразделения потребители	Конечный продукт	Валовый выпуск
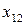
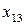
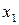
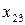
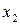
Материальные затраты
Амортизационные отчисления
Заработная плата
Прочие затраты и нераспределённая прибыль
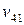
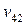
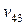
Валовые затраты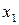

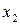
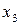
Численность работников 1-го, 2-го и 3-го структурного подразделения – 20, 30 и 35 человек, соответственно. Конечное потребление (расходы, выделяемые на производство продукции) – 700 руб. Подразделения 1 и 2 производят комплектующие, а подразделение 3 осуществляет сборку изделия. Известно, что подразделение 1 для подразделения 2 производит ресурсов в два раза больше, чем для подразделения 3 (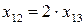). Определите бюджет каждого структурного подразделения на изготовление изделия А.

Решение. Составим систему балансовых уравнений:

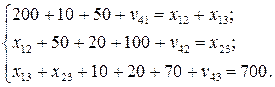
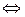
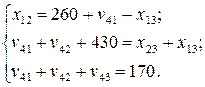
Таким образом, прочие затраты и нераспределенная прибыль составляют 170 руб. Распределим эту величину по подразделениям пропорционально численности работников.

Общая численность работников 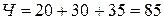чел. Соответственно: ; ; .

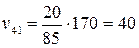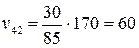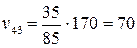Так как 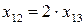, получим:

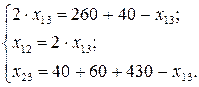
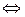
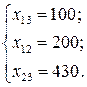
Баланс после проведенных расчётов представим в таблице 7.8.

Таблица 7.8

Стоимостной баланс изготовления детали А, руб.

Подразделения производители	Подразделения потребители	Конечный продукт	Валовый выпуск
Материальные затраты
Амортизационные отчисления
Заработная плата
Прочие затраты и нераспределённая прибыль
Валовые затраты

Данный стоимостной баланс можно использовать для определения бюджетов структурных подразделений. Например, бюджет третьего структурного подразделения на изготовление 100 изделий вида А составит:

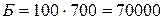руб.

Из своего бюджета третье структурное подразделение оплачивает первому подразделению за изготовление комплектующих деталей для 100 изделий: 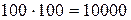руб., 2-му: 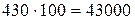руб. Оставшимися средствами коллектив (руководитель) подразделения может распоряжаться самостоятельно.

При составлении межотраслевого баланса в натуральном выражении исходят из того, что существует 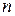отраслей, сектор конечного потребления и начальный ресурс – труд. Каждая отрасль использует в качестве ресурсов продукцию других отраслей и начальный ресурс (труд), выпуская при этом собственную продукцию, одна часть которой, в свою очередь, используется как производственный ресурс другими отраслями, а другая часть для конечного потребления.

Обозначим валовый выпуск 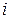-й отрасли 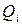, величину выпуска данной отрасли, используемую в качестве производственного ресурса в отрасли - 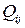, а величину выпуска, используемого для конечного потребления - 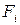. Количество начального ресурса, используемого -й отраслью обозначим 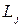. Тогда имеющиеся данные можно представить в табличном виде (таблица 7.9).

Таблица 7.9

Отрасли производства	Отрасли потребления	Конечное потребление	Валовый выпуск
			…
			…
…	…	…	…	…	…	…
			…
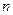
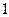
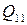
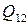
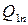
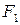
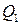
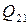
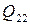
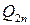
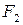
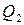
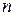
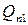
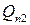
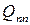
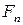
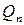
Начальный ресурс (труд)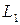

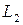
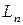
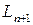
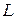
Система уравнений, характеризующая межотраслевые связи, имеет следующий вид:

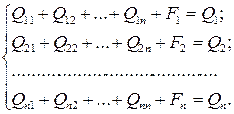
Норму затрат ресурса 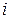-й отрасли на изготовление единицы продукции -й отрасли (технологический коэффициент продукта 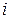-й отрасли в производстве -го товара) обозначим :

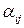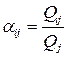, или .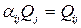

Подставляя технологические коэффициенты в систему уравнений, получаем:

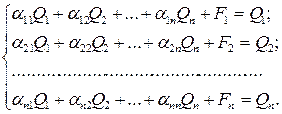
Для удобства проведения вычислений совокупность технологических коэффициентов представим в виде технологической матрицы:

.

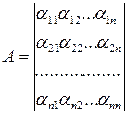После чего система уравнений в матричной форме принимает вид:

+ = .

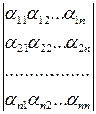
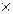
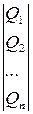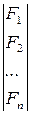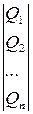Проведём преобразования:

= - = - .

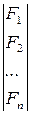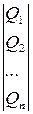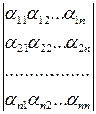
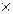
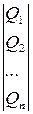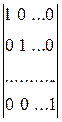
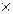
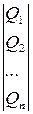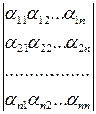
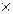
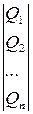Вычитая из единичной матрицы матрицу технологических коэффициентов, имеем:

= .

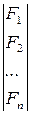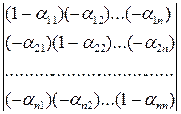
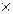
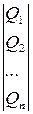Валовый выпуск отраслей, в зависимости от объёмов конечного потребления продукции:

= .

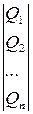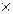
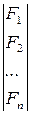Обозначив коэффициенты обратной матрицы 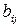, получаем:

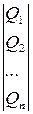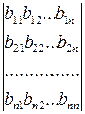
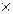
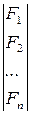= , или

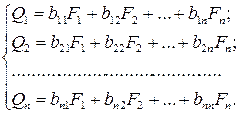
Коэффициенты 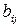показывают, сколько 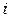-го ресурса необходимо использовать для производства единицы 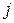-го товара для конечного потребления.

После определения валового выпуска отраслей можно оценить необходимое количество начального ресурса, для чего определим соответствующие технологические коэффициенты (прямые нормы затрат труда):

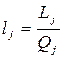, или .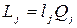

Количество начального ресурса:

.

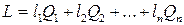Обозначим прямые и косвенные затраты начального ресурса, необходимые для производства единицы 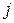-го товара конечного потребления 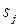, тогда:

,

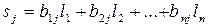и количество начального ресурса: .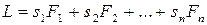

Пример. Баланс экономики страны, состоящей из пяти отраслей, в натуральном выражении представлен в таблице 7.10.

Таблица 7.10

Дата добавления: 2014-11-06