Методические указания к выполнению контрольной работы 1

В рекомендованных учебниках [1], [2], а также в руководствах [4] и [5] студенты найдут достаточное число примеров задач подобных тем, которые включены в контрольную работу. Поэтому ниже даны лишь необходимые краткие методические указания к решению задач контрольной работы.

Первую задачу (задачи 1 — 10) следует решить после изучения тем 1.1 и 1.2. Во всех задачах рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на нити. Требуется определить величину и направление реакций свя­зей для приведенной схемы. Таким образом, к точке Ов каждой задаче приложены три силы, из которых две неизвестны. Можно избрать три способа решения: аналитический, графический и геометрический. Для данного типа задач целесообразно использовать аналитический способ решения.

Последовательность решения задачи:

Пример 1. Определить величину и направление реакций свя­зей для схемы, приведенной на рис. 1, а под действием груза G = 30 кН. Проверить правильность определения реакций.

Решение. 1. В задаче рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести.

2. Приложим к точке 0 активную силу, которой является соб­ственный вес тела G. Направим ее вниз (рис. 1, б).

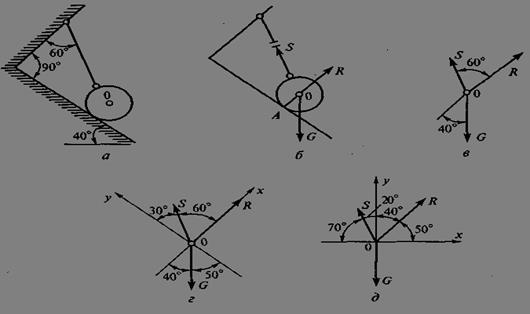
Рис. 1

3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обо­значим ее R) проходит по нормали к плоскости в точке А, а ре­акция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересе­каться в точке0.

Изобразим действующие силы в виде системы трех сходя­щихся сил на отдельном чертеже (рис. 1, в).

4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. 1, г). Определим углы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, а сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было бы другим.

5. Составим сумму проекций всех сил на оси координат:

1) ∑ Х = R + S cos 60° - G ∙cos40° = 0;

2) ∑ У = S^∙cos30^o – G ∙ cos50⁰ = 0.

Решим систему уравнений. Из второго уравнения находим

S = 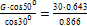= 22,27 кН.

Из первого уравнения находим

R = G cos 40° - S cos 60° = 30 ∙ 0,766 - 22,27· 0,5 = 11,84 кН.

6. Проверим решение, для чего расположим оси координат,
как показано на рис. 1, д. Составим уравнения равновесия для
вновь принятых осей:

1) ∑ X = R cos 50° - S cos 70° = 0;

2) ∑ У = R cos40°+Scos20°-G=0.

Решим систему уравнений способом подстановки. Из первого уравнения найдем R.

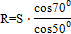
Подставим это выражение во второе уравнение:

,

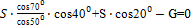откуда

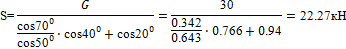
Теперь найдем R:

= 11,84 кН.

Очевидно, что при расположении осей, как показано на рис. 1, д, вычисления оказались более сложными.

Ответ: R= 11,84 кН; S = 22,27 кН.

Вторую задачу (задачи 11—20) следует решать после изучения тем 1.3 и 1.4. Во всех задачах требуется определить реакции опор балок. Учащимся необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротив­лению материалов и деталям машин.

Последовательность решения задачи:

1. Изобразить балку вместе с нагрузками.

2. Выбрать расположение координатных осей, совместив ось х с балкой, а ось у направив перпендикулярно оси х.

3. Провести необходимые преобразования заданных активных сил: силу, наклонённую к оси балки под углом α, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределённую нагрузку – её равнодействующей, приложенной в середине участка распределения нагрузки.

4. Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат.

5. Составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор.

6. Проверить правильность найденных опорных реакций по уравне­нию, которое не было использовано для решения задачи.

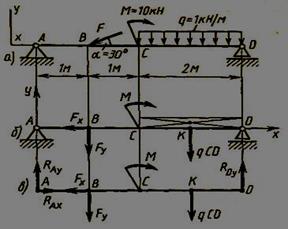Рис. 2

Пример 2. Определить реакцию опор балки (рис. 2, а). Решение.1.Изобразим балку с действующими на нее нагруз­ками (рис. 2, а). 2. Изображаем оси координат х и у. 3. Силу F заменяем ее составляющими Fx=Fcosa и Fy = Fsin а. Равнодействующая q • CD равномерно распределенной нагрузки приложена в середине участка CD, в точке К (рис. 2,б).

4. Освобождаем балку от опор, заменив их опорными реакциями (рис. 2, в).

5. Составляем уравнения равновесия статики и определяем не­известные реакции опор.

Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:

∑M_A(F_i)= F_y·AB - M - q·CD∙AK + R_D·AD = O;

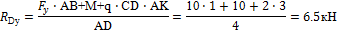
Определяем другую вертикальную реакцию:

∑M_D(F_i)= - R_Аy·AD + F_у∙ВD - M + q·CD∙KD = O;

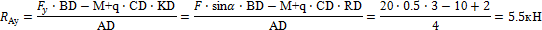
Определяем горизонтальную реакцию:

∑Х_i = R_Ax – F_х = 0; R_Ax = F_х = F cos a = 20 · 0,866 = 17,3 кН.

6. Проверяем правильность найденных результатов:

∑Y_i = R_Aу – F_у - q∙CD + R_Dу= 5,5 – 10 - 2 + 6,5 = 0.

Условие равновесия ∑Y_i = 0 выполняется, следовательно, реакции oпор найдены верно.

Ответ: R_Ax=17,3 кН; R_Aу=5,5 кН; R_Dу=6,5 кН.

Третью задачу (задачи 21—30) следует решать после изучения темы 1.5.

Последовательность решения задачи:

1. Изобразить на рисунке тело, равновесие которого рассматри­вается, с действующими на него активными силами и реакциями
опор и выбрать систему осей координат.

2. Из условия равновесия вала, имеющего неподвижную ось, определить значение силы F₂, после чего вычислить значение силы F_r2.

3. Составить шесть уравнений равновесия.

4. Решить уравнения и определить реакции опор.

5. Проверить правильность решения задачи.

Пример 3. На вал (рис. 3, а) жестко насажены шкив 1 и колесо 2. Определить силы F₂, F_r2 = 0,4 F₂, а также реакции опор А и В, если F₁ = 100 Н.

Решение. 1. Изображаем вал со всеми действующими на него силами, а также оси координат (рис. 3, б).

2. Определяем F₂ и Fr₂. Из условия равновесия вала, имеющего
неподвижную ось:

∑М_z (F_i)=0;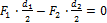

3. Составляем шесть уравнений равновесия:

∑M_х(F_i)= 0; ∑М_х= R_Ву∙АВ – F₂·АD = 0; (1)

∑M_у(F_i)= 0; ∑М_у = - 3F₁ ∙AC - F_r2·AD + R_Bх∙AB = 0; (2)

∑M_х1(F_i)= 0; ∑М_х1 = - R_Aу ·AB+ F₂·DB = 0; (3)

∑M_у1(F_i)= 0; ∑М_у1 = - R_Aх ·AB+3F₁· CB -F_r2·DB =0; (4)
∑Х_i = 0; ∑Х_i =3F₁ + F_r2 - R_Aх - R_Bх = 0; (5)

∑Y_i = 0; ∑Y_i = R_Aу - F₂ + R_Ву = 0 (6)

4. Решаем уравнения (1), (2), (3), (4) и определяем реакции опор:

из (1)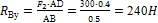

из (2) 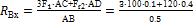= 156 Н;

из (3)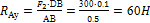

из (4) 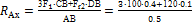= 264 Н.

5.Проверяем правильность найденных реакций опор. Используем уравнение (5):

∑Х_i =3F₁ + F_r2 - R_Aх - R_Bх = 300+120 – 264 – 156 = 0,

следовательно, реакции R_Ax и R_Bx определены верно. Используем урав­нение (6):

∑Y_i = R_Aу - F₂ + R_Ву = 60 – 300 + 240= 0,

∑Y_i = 0, следовательно, реакции R_Ay и R_Вy определены верно.

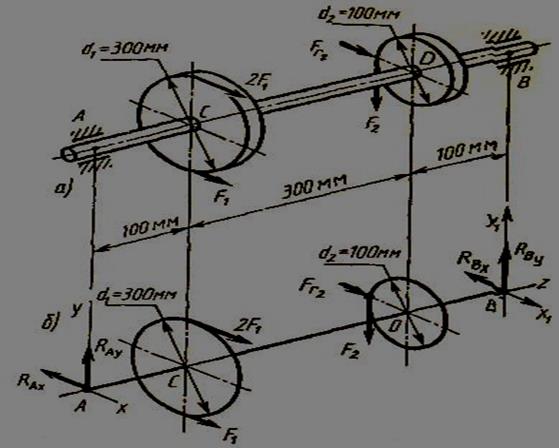
Рис. 3

Ответ: R_Ax=264 Н; R_Aу=60 Н; R_Вx=156 Н; R_Ву=240 Н.

Данную задачу можно решать другим методом: спроектировать тело со всеми действующими на него активными силами и реакциями опор на три координатные плоскости, чтобы проще было составлять уравнения равновесия. Этот метод подробно рассмотрен в руководстве [5].

Четвертую задачу (задачи 31—40) следует решать после изучения темы 1.6.

Пример 4. Определить координаты центра тяжести сечения, составленного из профилей проката, как показано на рис. 4, а. Сечение состоит из двутавровой балки № 33, швеллера № 27, двух уголков 90x56x6 мм и листа сечением 12x180 мм.

Решение. 1. Разобьем сечение в соответствии с профилями про­ката и обозначим их 1, 2, 3, 4, 5.

2. Пользуясь табл. 1, 2 и 3 Приложения, укажем центры тяжести каждого профиля и обозначим их С₁, С₂, С₃, С₄ и С₅.

3. Выберем систему осей координат. Ось у совместим с осью симметрии, а ось х направим перпендикулярно оси у и проведем через центр тяжести двутавровой балки.

4. Выпишем формулы для определения координат центра тяже­сти сечения:

х_С = 0, так как ось у совпадает с осью симметрии;

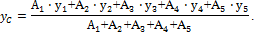
Учитывая, что А₂ = А₃, а также, что у₂ = у₃, получим:

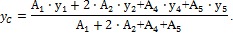
Определим площади и координаты центров тяжести отдельных профилей проката, используя сечение и табл. 1, 2 и 3 приложения:

А₁ = 35,2 см²; А₂ = А₃ = 8,54 см²; А₄ = 53,8 см²; А₅ = 1,2 • 18 = 21,6 см²;

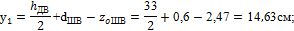
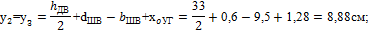
у₄ = 0, так как ось х проходит через центр тяжести двутавра;

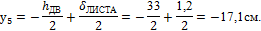
5. Заполним следующую таблицу:

№ фигуры, название фигуры	хСi, см	уСi, см	Аi, см^2
1, швеллер		14,63	35,2
2, уголок неравнополочный		8,88	8,54
3, уголок неравнополочный		8,88	8,54
4, швеллер			53,8
5, лист		- 17,1	21,6
∑ Аi	127,7

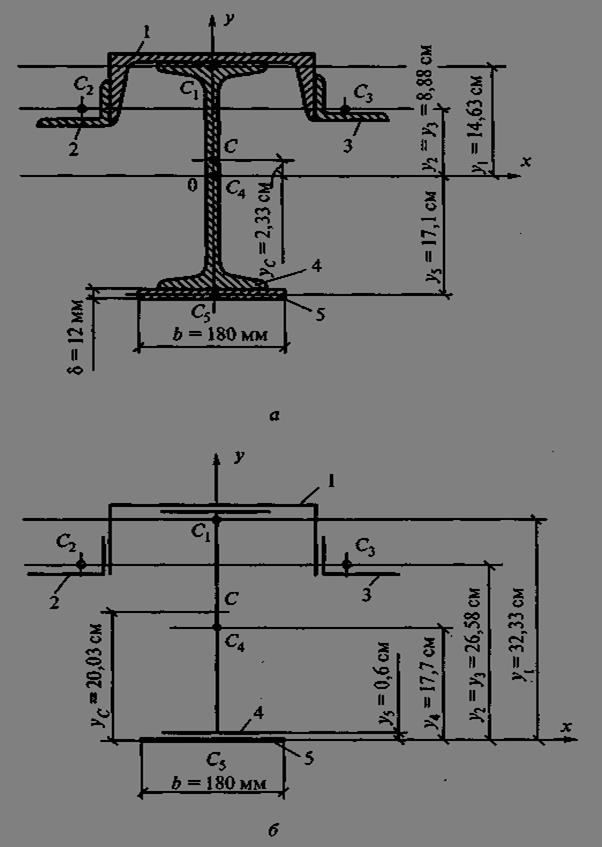Рис. 4

Подставим полученные значения в формулу для определения у_с:

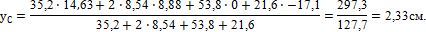
Укажем положение центра тяжести сечения С (см. рис. 4, а).

Ответ: С (0; 2,33).

Пятую задачу (задачи 41—50) следует решать после изучения тем 1.7, 1.8, 1.9.

Для всех номеров пятой задачи применяется понятие средней скорости, которая (независимо от вида движения) определяется как результат деления пути, пройденного точкой (или телом) по всей траектории движения, на все затраченное время.

Решая пятую задачу, рекомендуется разбить весь пройденный путь при движении точки (или тела) на участки равномерного, равно­ускоренного или равнозамедленного движения в зависимости от усло­вия данной задачи.

В задачах 41, 43, 45, 47 и 49 рассматривается как равномерное, так и равнопеременное движение точки по траектории, составленной из прямолинейных участков и дуг окружности. В этих задачах определяем требуемые параметры движения точки с учетом естественного способа задания движения (см. пример 5).

Касательное a_t и нормальное а_n ускорения точки являются глав­ными кинематическими величинами, определяющими вид и особенности движения точки. Причем 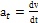, 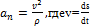- линейная скорость точки в данный момент времени; ρ — радиус кривизны траектории.

В случае равномерного прямолинейного движения

а_t = 0; а_n = 0; v = const;

уравнение движения s = s_o + vt или при s_o = 0, s = vt.

В случае равномерного криволинейного движения

а_t = 0; а_n ≠ 0; v = const;

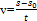или , ;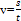

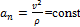при движении по дуге окружности ρ = r = const.

В случае неравномерного прямолинейного движения

а_t ≠ 0; а_n = 0; а = а_t = const;

s = s_о + v_ot+ 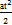; v = v_o + at.

В случае неравномерного криволинейного движения
а_t ≠ 0; а_n = 0. При а_t = const движение является равноперемен­ным криволинейным. Если а_t >0 — равноускоренное движение, а_t <0 —
равнозамедленное движение.

Уравнение равнопеременного движения независимо от траектории
имеет вид

s = s_о + v_ot+ 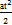, (1)

где s_o — начальное расстояние точки в момент начала отсчета; v_o — начальная скорость.

v = v_o + a_t t (2)

Если неизвестные входят в уравнения (1) и (2), то для удобства решения задачи пользуемся вспомогательными формулами:

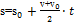(3)

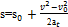(4)

При s_o = 0 и v_o= 0 (равнопеременное движение из состояния покоя) формулы (3) и (4) имеют такой вид:

s = 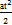(5)

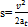(6)

При любом криволинейном движении модуль полного ускорения точки в данный момент времени

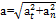(7)

В задачах 42, 44, 46, 48 и 50 рассматривается вращательное движение тела (см. пример 6). Решая эти задачи, необходимо уметь переходить от числа оборотов к радианному измерению угла поворота и наоборот:

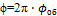(8)

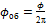(9)

где φ — угол поворота тела, φ _об — число оборотов.

Переход от одних единиц угловой скорости к другим:

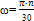рад/с (10)

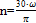об/мин. (11)

При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на оси вращения тела (см. рис. 5).

s=r ·φ (12)

v = r ·ω (13)

a_t = r ·ε (14)

a_n = ω² · r (15)

где s — расстояние, пройденное точкой по дуге окружности (˘А₁А₂ = s, смотри рис. 5);

φ — угол поворота тела, рад;

r — расстояние точки до оси вращения тела;

ω — угловая скорость;

ε — угловое ускорение;

v — окружная скорость точки в данный момент времени;

а_t — касатель­ное ускорение точки;

а_n — нормальное ускорение точки.

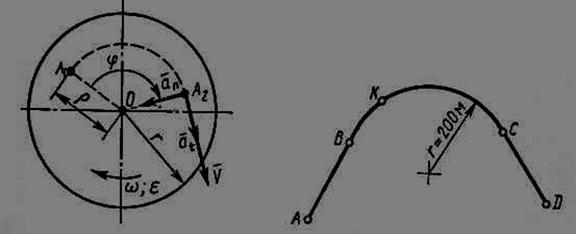Рис. 5 Рис. 6

При равномерном вращении

φ = φ₀ + ω·t (16)

При φ₀= 0 φ = ω·t (17)

ω = φ / t (18)

При равнопеременном вращении тела (ε>0 — равноускоренное вра­щение; ε<0 — равнозамедленное вращение):

φ = φ₀ + ω₀·t + 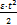(19)

ω = ω₀ + ε·t (20)

Для удобства решения задач из уравнений (19) и (20) получаем

φ = φ₀ + 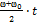(21)

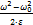φ = φ₀ + (22)

Для случая равнопеременного вращения, начавшегося из состояния по­коя (при q φ₀= 0 и ω₀= 0), формулы (21) и (22) имеют вид

φ = 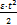(23)

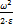φ = (24)

Пример 5. Точка начала двигаться равноускоренно по прямой из состояния покоя и через 25 с ее скорость стала равна 50 м/с. С этого момента точка начала равнозамедленное движение по дуге окружности радиуса r = 200 м и через 20 с ее скорость снизилась до 10 м/с. После этого точка продолжила свое движение с этой скоростью по прямой и через 5 с внезапно остановилась.

Определить: 1) среднюю скорость точки на всем пути; 2) полное ускорение точки через 10 с после начала ее равнозамедленного движе­ния по окружности.

Решение. 1. Представим траекторию движения точки, как пока­зано на рис. 6. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.

2. Рассмотрим движения точки по отрезку АВ:

v_В = v_А + a_АВ ·t_АВ ; v_А=0; a_АВ=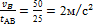

s_АВ = .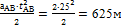

3. Рассмотрим движение точки по дуге ВС:

v_B = 50 м/с; v_С =10 м/с; t_BС = 20 с

v_С = v_В + a _{t ВС} ·t_ВС

a _{t ВС}=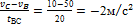
s_BС=v_B·t_BС + 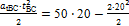=600 м.

4. Рассмотрим движение точки на отрезке CD:

v_c= 10 м/с; t_CD= 5 с;

s_cd= v_c·t_CD= 10·5 = 50 м.

5. Определим среднюю скорость точки на всем пути по траектории
движения ABCD (см. рис. 6):

;

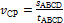s _ABCD= s _AB + s_BC + s_CD = 625 + 600 + 50 = 1275 м;

t_ABCD = t_AB+t_BC + t_CD = 25 + 20 + 5 = 50 с;

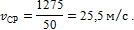
6. Определим значение полного ускорения точки через 5 с после начала равнозамедленного движения (см. положение К на рис. 6)

v_В =50м/с; t_К =5с; v_К = v_B + a_{t BС} · t_K= 50—2·5=40 м/с;

a_{t BС} = - 2 м/с²;

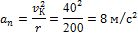
Полное ускорение:

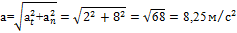
Пример 6. Тело начало вращаться из состояния покоя и через 15 с его угловая скорость достигла 30 рад/с. С этой угловой скоростью тело вращалось 10 с равномерно, а затем стало вращаться равнозамедленно в течение 5 с до полной остановки.

Определить: 1) число оборотов и среднюю угловую скорость тела за все время вращения; 2) окружную скорость точек тела, расположен­ных на расстоянии r = 0,5 м от оси вращения тела через 5 с после начала движения.

Решение. 1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного дви­жения. Определим параметры вращательного движения тела по этим участкам.

2. Равноускоренное вращение (участок I):

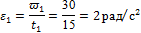
φ₁ =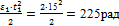

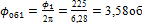
3. Равномерное вращение (участок II):

ω_II = ω_I; φ_II = ω_II · t_II =30·10=300 рад

φ_обII =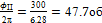

4. Равнозамедленное вращение (участок III):

ω_III = ω_II = ω_I

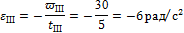
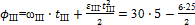= 75 рад

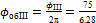= 11,9 об

5. Определим полное число оборотов тела за все время вращения:

φ_обI + φ_обII + φ_обIII = 35,8 + 47,7 + 11,9 = 95,4 об.

6. Определим среднюю угловую скорость тела за все время враще­ния:

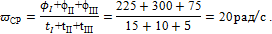
6. Определим окружную скорость точек тела, расположенных на
расстоянии r = 0,5 м от оси вращения через 5 с после начала движе­ния тела:

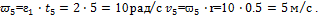
Шестая задача (задачи 51—60) связанная с определением работы и мощности либо при поступательном, либо при вращательном движе­нии. Задачи следует решать, изучив темы 1.14 и 1.15, а также повторив материал о трении скольжения и качения. Решая данные задачи, необходимо внимательно следить за тем, чтобы числовые значения величин были выражены в единицах СИ.

В учебниках [1], [2], а также в руководстве [6] достаточно под­робно разобраны методы решения подобных задач.

Приведем основные формулы, необходимые для вычисления работы и мощности. Работа постоянной силы F на прямолинейном пути:

W = F·s·cosα, где α — угол между направлением силы и перемещения.

Работа силы тяжести: W=±G·H, где Н — разность уровней движущейся точки.

Работа пары сил: W=M·φ, где М — момент пары; φ —угол ее поворота.

В СИ работа выражается в джоулях (Дж):

1 Дж = 1 Н·м; 1 кДж= 10³ Дж.

Мощность определяется по формуле

,

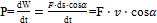при α=0 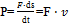, где v — скорость точки.

При вращательном движении Р=М·ω или М = Р/ω,

где М — вращающий момент; ω — угловая скорость.

В СИ мощность выражается в ваттах: 1 Вт = 1 Дж/с; 1 кВт = 10³ Вт.

Механический коэффициент полезного действия:

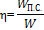
где W_П.С. — работа сил полезных сопротивлений; W — вся совершенная работа, или η = 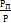, где Р_П — полезная мощность; Р — вся затрачен­ная мощность.

Дата добавления: 2014-11-06