
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Природа эвристик
|
|
|
|
Эвристики планирования
Другой класс широко применимых эвристик, увеличивающих избирательность генераторов решений, составляют эвристики, которые идут под рубрикой «планирование». Рассмотрим лабиринт длиной в q шагов с m альтернативами в каждой точке выбора. Предположим, что вместо сигналов, обозначающих правильный путь в каждой точке выбора, есть лишь сигналы в каждой второй точке. Тогда задача прохождения лабиринта легко может быть расчленена на ряд подзадач достижения тех точек выбора, которые отмечены сигналами.
Такая группа подзадач составит план. Вместо начальной задачи прохождения лабиринта длиной в k шагов перед субъектом,
решающим проблему, встанет задача прохождения k / 2 лабиринтов, каждый из которых длиной в два шага. Ожидаемое число путей, которые должны быть обследованы при решении первой проблемы, будет, как и раньше, равно 1/2 mk Ожидаемое число проб при решении второй проблемы
1/2 (k/2) m2
Если начальный лабиринт будет иметь в длину 6 шагов при двух альтернативах в каждой точке, среднее число требуемых проб будет cокращено с 32 до 6, к которым, в свою очередь, следует добавить усилия, необходимые для того, чтобы найти план.
Мы используем подобный метод планирования, когда путешествуем. Сначала мы набрасываем общий маршрут от города к городу, затем, имея в виду эти города как подцели, мы решаем подзадачи, как попасть из одного в другой.
Мы видели, что успех лица, решающего задачу, которое сталкивается со сложной проблемой, основан прежде всего на его способности правильно выбирать для обследования небольшую часть общего проблемного лабиринта. Процессы, которые осуществляют этот выбор, мы обозначаем как эвристики. Мы видели, что большинство эвристик основано на стратегии, при которой последующий поиск изменяется как функция информации, полученной в предыдущем поиске; и мы рассмотрели несколько наиболее значительных и эффективных типов эвристик, с которыми мы столкнулись в своих попытках имитировать процессы решения задачи человеком. Мы придали операциональный смысл соответствующим терминам путем выделения реальных процессов, которые осуществлял бы «логик-теоретик» или машина, играющая в шахматы. Мы обращались к протоколам испытуемых для подтверждения положения о том, что эти процессы действительно имеют место в поведении человека при решении задачи. Мы разработали также количественные приемы оценки сокращения поисковых действий, вызванных избирательностью этих эвристик, и использовали эти оценки для определения способности людей и машин, имитирующих их, путем использования тех же самых процессов решать конкретные задачи.
П. Линдсей, АНАЛИЗ ПРОЦЕССА
Д. Норман РЕШЕНИЯ ЗАДАЧ
Норман (Norman) Дональд (род. 25 декабря 1935) — американский психолог, один из крупных современных исследователей в области изучения познавательных процессов. Профессор Калифорнийского университета. Автор книги «Память и внимание» («Memory and Attention». N. Y., 1969), редактор и участник фундаментальной коллективной монографии «Модели человеческой памяти» («Models of Human Memory». N. Y.—L., 1970). Вместе с Питером Линдсеем (Lindsay) (университет Торонто, Канада) Д. Норман является также автором учебника по психологии, в котором последовательно проводится теоретико-информационный подход к анализу познавательных процессов («Human Information Processing». N. Y.—L., 1972). В отрывке из этой книги (печатается по русскому переводу — М., 1974) рассматриваются некоторые приемы изучения и описания процесса решения задач, характерные для направления «эвристического программирования» на современном этапе.
Что именно следует сделать, чтобы решить некоторую задачу? Мы рассмотрим стратегии и процедуры, обычно используемые людьми. Прежде всего задачи бывают двух основных типов: четко поставленные и нечетко поставленные. В четко поставленной задаче цель ясно сформулирована. Вот примеры таких задач:
1) как наилучшим образом проехать в другой конец города, если все главные улицы закрыты для транспорта по случаю парада;
2) как решить шахматную задачу, помещенную во вчерашней газете: белые начинают и делают мат в пять ходов.
В этих задачах, помимо ясной цели, имеется определенный способ судить о том, идет ли процесс решения в надлежащем направлении. И хотя в жизни, пожалуй, чаще встречаются задачи, поставленные нечетко, у нас есть все основания сосредоточить наше исследование на четко поставленных задачах. Наша цель — выяснить, какие процессы использует человек, добивающийся решения той или иной задачи. Мы хотим понять, как он строит внутреннюю модель задачи, какую стратегию избирает, каким правилам следует. Мы хотим узнать, какие средства позволяют ему успешно продвигаться к решению. Результаты этих исследований должны быть приложимы к решению любых задач, поставлены ли они четко или нечетко.
Лучше всего, вероятно, начать с исследования конкретной задачи.
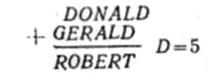
Данная задача относится к классу криптоарифметических задач. В приведенном выражении использовано десять букв, каждая из которых соответствует определенной цифре. Задача состоит в том, чтобы найти для каждой буквы соответствующую ей цифру, так чтобы получившиеся цифры удовлетворяли сформулированному арифметическому равенству.
Мы разберем небольшую часть словесного отчета одного испытуемого, пытавшегося решить эту задачу. Дав пояснения к задаче, сходные с приведенными выше, его просили думать вслух в процессе поиска решения. Испытуемый впервые пытался решить такого рода задачу. Полная запись его высказываний в течение 20 мин, затраченных на решение, составляет протокол объемом около 2200 слов (задача, ее анализ и приводимые ниже цитаты из протокола заимствованы из работы Ньюэлла, 1967).
Протокол решения задачи «DONALD+ GERALD»
Каждая буква имеет одно и только одно числовое значение? (Это был вопрос к экспериментатору, который ответил: «Одно числовое значение»). Имеется десять различных букв, и каждая из них имеет одно числовое значение.
Букв две, и каждая из них соответствует 5; значит, Т есть нуль. Так что, я думаю, можно для начала вписать это в текст задачи. Я вписываю: 5,
5 и 0.
Посмотрим, есть ли у нас еще Т. Нет. Зато есть еще одно D. Значит, я могу поставить 5 с другого края.
Дальше, у нас есть два А и два L — каждая пара в одном разряде и еще три R. Два L равны одному Р. Разумеется, я перенес 1 во второй разряд, откуда следует, что Р должно быть нечетным числом, поскольку сложение двух одинаковых чисел дает четное число, а 1 — число нечетное. Так что Р может быть равно 1 или 3, но не.5, не 7 и не 9.
(Здесь наступила долгая пауза, и экспериментатор спросил: «О чем вы сейчас думаете?»).
Теперь G. Раз R — нечетное число, a D равно 5, то О должно быть четным. Я смотрю на левый край примера, где складывается D с G. Ах, нет, возможно, сюда надо прибавить еще 1, если мне пришлось бы перенести 1 из предыдущего разряда, где складываются О и Е. Пожалуй, мне нужно на минуту отвлечься от этого.
Вероятно, лучше всего решать эту задачу, перебирая различные возможные решения. Но я не уверен, что это окажется самым легким путем.
Цитированный текст будет служить нам первичным материалом для анализа процесса решения. Первое впечатление от такого протокола — что испытуемый не подходит к задаче прямо и непосредственно. Он накапливает информацию и проверяет различные гипотезы, выясняя, к чему они приводят. Он часто заходит в тупик и, отступая, пробует другой путь. Взгляните на протокол. Испытуемый начинает энергично и сразу обнаруживает, что Т равно нулю.
Букв D две, и каждая из них соответствует 5; значит, Т есть нуль. Так что, я думаю, можно для начала вписать это в текст задачи. Я вписываю: 5, 5 и 0.
После этого он выясняет, можно ли использовать где-нибудь в тексте задачи свое знание, что Т равно нулю, a D равно 5. Ищет Т.
Посмотрим, есть ли у нас еще Т. Нет. Эта попытка не удалась. Ну, а как D? Зато есть еще одно D. Значит, я могу поставить 5 с другой стороны.
Отметив это обстоятельство, испытуемый обнаруживает другое место в тексте задачи, которое кажется перспективным.
Дальше, у нас есть два А и два L — каждая пара в одном разряде — и еще три R. Два L равны одному R. Разумеется, я перенес 1 во второй разряд. Откуда следует, что R должно быть нечетным числом.
Хотя испытуемый уже пришел к заключению, что R — нечетное число, он вновь возвращается к этому вопросу, как бы проверяя свой вывод:
...поскольку сложение двух одинаковых чисел дает четное число, а 1 — число нечетное.
На этот раз он продолжает рассуждение несколько дальше и конкретно, перечисляет возможные числа.
Так что R может быть равно 1 или 3, но не 5, не 7 и не 9.
После долгой паузы испытуемый, однако, отказывается от этого пути по понятной причине: нет очевидного способа выбрать значение R из возможных вариантов. Он опять возвращается к идее о нечетности R. Дает ли это какую-нибудь информацию относительно G?
Теперь G. Раз R — нечетное число, a D равно.5, G должно быть четным.
Этого краткого анализа отчета о первых пяти минутах эксперимента достаточно для того, чтобы обнаружить некоторые общие закономерности в поведении испытуемого при решении задачи. Однако словесными протоколами пользоваться неудобно. Для подробного исследования процесса решения задачи нужно иметь какой-то метод представления происходящих событий. Полезно строить визуальные изображения последовательности операций, совершаемых во время решения задачи. Одним из методов, пригодных для этой цели, является граф решения задачи, разработанный А. Ньюэллом (Саймон и Ньюэлл, 1971).
Исследуя протокол, мы видели, что испытуемый постепенно накапливает информацию о задаче, применяя определенные правила или стратегии. Он производит разного рода операции над этой информацией и над текстом задачи; в результате его
Знания возрастают. Вся информация о задаче, которой испытуемый располагает в данный момент, называется его состоянием осведомленности. Всякий раз, как он применяет некоторую операцию к некоторому новому факту, состояние осведомленности изменяется.

Описание поведения человека при решении задачи должно, таким образом, отражать это последовательное продвижение от одного состояния осведомленности к другому. Будем изображать графически состояние осведомленности прямоугольником, а операцию, переводящую испытуемого из одного состояния осведомленности в другое, — в виде стрелки (рис. 23).
Теперь протокол можно представить в виде прямоугольников, соединенных стрелками: последние показывают путь, проходимый испытуемым через последовательные состояния осведомленности.
Граф задачи «Donald+Gerald». Несколько высказываний в начале словесного отчета отражают просто проверку испытуемым своего понимания условий задачи. Само рассуждение начинается лишь с фразы:
Букв D две и каждая из них соответствует 5; значит, Т есть нуль.
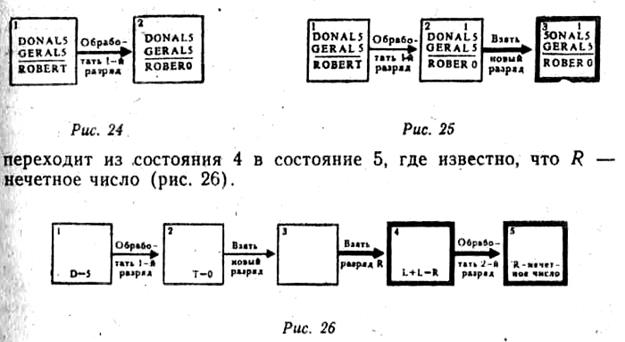
Испытуемый, несомненно, перерабатывает информацию, содержащуюся в этом разряде, где показано, что D+D=T. Назовем эту операцию обработкой 1-го разряда. Эта операция переводит испытуемого из начального состояния осведомленности (в котором он знает, что D=5) в новое состояние, в котором он знает, кроме того, что Т=0. Известно ли испытуемому также, что необходимо сделать перенос в следующий, 2-й разряд? Забегая вперед, читаем: «Разумеется, я перенес 1». Таким образом, это испытуемому известно. К настоящему моменту наш граф решения задачи насчитывает два состояния осведомленности. (рис. 24)
Следующие несколько фраз протокола, по существу, резюмируют сведения, известные испытуемому к данному моменту. Затем делается попытка найти другие разряды, содержащие Т или D. Первое применение операции взять новый разряд (с Т) безуспешно; второе дает положительный результат: находится другой разряд, содержащий D. Граф решения задачи получил некоторое приращение (рис. 25), на этом рисунке прямоугольник, которого не было на предыдущей схеме, обведен жирной линией.
Теперь испытуемый решает еще раз взять новый разряд, пробуя сначала 3-й разряд, а затем 2-й.
Дальше, у нас есть два А и два L — каждая пара в одном разряде — и еще три R.
Это приводит его к тому пункту рассуждения, в котором имеет смысл обработать 2-й разряд. В результате обработки он
Обратный ход. Теперь испытуемый возвращается к пройденному состоянию. Обратите внимание на последовательность Действий. Сначала, в состоянии 5, он говорит:
Два L равны одному R. Разумеется, я перенес 1 во второй разряд, откуда следует, что R должно быть нечетным числом.
Но затем испытуемый решает конкретно выяснить возможные числовые значения буквы R: для этого он возвращается в состояние 4 и испытывает новый подход.
...поскольку сложение двух одинаковых чисел дает четное число, а 1 — число нечетное. Так что R может быть равно 1 или 3, но не 5, не 7 и не 9.
На графе этот обратный ход отображается таким образом, что стрелка к следующему, 6-му состоянию идет из состояния 4 (рис. 27). Состояние 6 — это, собственно, то же состояние 4, только в более поздний момент времени. В состоянии 7 испытуемый вновь воспроизвел тот факт, что R нечетно, а в состоянии 8 он методически перечисляет все подходящие и неподходящие нечетные числа.
Последующая часть текста протокола дает пример того, какие трудности испытывает экспериментатор, «добывая» протокол. Испытуемый молчит, так что экспериментатор вынужден вмешаться и просить его говорить. В результате мы не имеем явных свидетельств того, как использованы возможные числовые значения R. Вместо этого мы видим, что процесс решения снова идет вспять; на этот раз испытуемый обращается к 6-му разряду и исходя из того, что R — число нечетное, a D равно 5, заключает, что G должно быть четным числом, это приводит нас к состоянию 10.
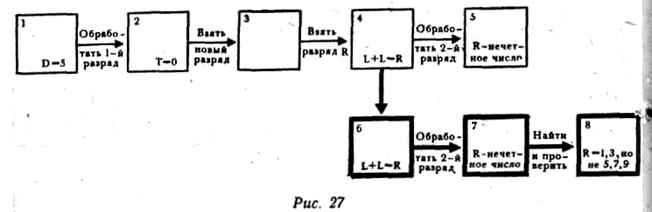
Теперь G. Раз R — нечетное число, a D равно 5, то G должно быть четным.
Хотя этот вывод неверен, тем не менее в момент, представляемый состоянием 10, он отвечает действительному состоянию осведомленности испытуемого (рис. 28). В данном случае возможность того, что G не обязательно четно, приходит ему в голову довольно скоро.
Я смотрю на левый край примера, где складывается D с О.
Ах, нет, возможно, сюда надо прибавить еще 1, если мне пришлось бы перенести 1 из предыдущего разряда, где складываются О и Е. Пожалуй, мне нужно на минуту отвлечься от этого.
Последняя фраза указывает, что испытуемый вновь хочет приступить к обработке 6-го разряда и в результате оказывается в состоянии 12 (признает возможность переноса), а затем решает еще раз вернуться назад, отказавшись от полученной ранее численной оценки для G (четное число). На этом мы заканчиваем анализ фрагмента протокола. Соответствующий фрагмент графа решения показан, на рис. 28.
Рассмотрим теперь, чем отличаются друг от друга три(различных «пространства» задачи: внутреннее, отраженное в протоколе и внешнее. Испытуемый решает задачу про себя в соответствии с некоторыми общими стратегиями и посредством операций, которые, будем надеяться сходны со стратегиями и операциями, представленными в графе решения задачи. Это решение представлено во внутреннем пространстве, прямое наблюдение которого для нас невозможно. Словесные высказывания, делаемые испытуемым в ходе решения задачи, — протокол — это запись в протокольном пространстве. И, кроме того, продвигаясь к решению, испытуемый записывает те или иные выражения и выполняет некоторые действия, порождая тем самым внешнее пространство.

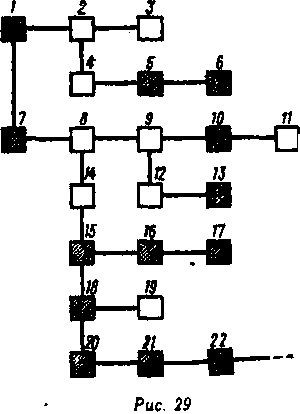
Посмотрим, как можно соотнести эти три пространства друг с другом. Внутреннее пространство можно представить схематически в виде графа решения задачи. На рис. 29 показан пример внутреннего пространства, в котором представлено 22 состояния. Но испытуемый может объявить в своем протоколе лишь некоторые из этих внутренних состояний — они показаны заштрихованными прямоугольниками. В данном случае в протоколе представлено 13 из 22 состояний внутреннего пространства.
Понятно, что произошло. В протокольном пространстве дело обстоит так, как если бы от состояния 1 испытуемый перешел непосредственно к состоянию 5 и 6. Промежуточные состояния 3 и 4, а также тупиковая линия к состоянию 3 выпали совершенно. И вдобавок состояние 10 и состояние 13 следуют за состоянием 7. Часто при анализе протокола может быть обнаружена
нехватка каких-то звеньев. Окончательный граф, реконструированный на основании протокола, действительно имеет много общего с графом внутренних состояний, однако он определенно не является полным отображением процессов, происходивших в ходе решения задачи. Проходя через последовательность внутренних состояний, испытуемый порождает на уровне поведения сокращенную версию внутренних процессов мышления.
Граф решения — один из методов разложения процесса решения этой задачи на этапы, выделения в процессе его отдельных шагов. В нем графически представлено чередование успехов и неудач, характерных для хода решения всякой задачи. Эта общая форма анализа и изображения поведения представляется применимой к широкому разнообразию проблемных ситуаций. Понятно, что конкретные правила, используемые человеком, зависят от характера решаемой задачи, однако общая структура его поведения в ходе решения задачи всегда одинакова. Человек разбивает задачу на множество более простых промежуточных задач, т. е. ставит перед собой промежуточные вопросы. В любой заданный момент достигнутый им успех можно охарактеризовать с помощью понятия осведомленности. Человек переходит от одного состояния осведомленности к другому через попытки применения одной из операций, выбираемых из имеющегося у него небольшого выбора. Анализируя сам подход к решению задачи, можно выделить две различные стратегии.
В большинстве случаев решение задачи включает момент прямого поиска. Другими словами, человек сначала испытывает какой-то метод подхода к задаче, а затем смотрит, продвинулся ли он вперед в результате его применения. Если да, то он продолжает идти в том же направлении от достигнутого пункта. Здесь важно то, что поиск от начала до конца осуществляется простыми, прямыми шагами.
Второй подход представлен обратным поиском. Здесь человек рассматривает искомое решение, задаваясь вопросом: какой предварительный шаг необходим для того, чтобы прийти к нему? После определения этого шага определяется шаг, непосредственно ему предшествующий, и т. д., в лучшем случае — вплоть до отправной точки, заданной в постановке исходной задачи. Обратный поиск чрезвычайно полезен в некоторых визуальных задачах, вроде нахождения по карте пути из одного пункта в другой.
При обратном поиске продвижение к цели осуществляется небольшими шагами. Определяется некоторая промежуточная цель и делается попытка решить промежуточную задачу. Здесь вступает в действие одна, вероятно наиболее сильная стратегия, так называемая стратегия сопоставления средств и целей. При этом сопоставлении цель (ближайшая промежуточная цель) сравнивается с наличным состоянием осведомленности. Проблема состоит в нахождении оператора — средства, уменьшающего разрыв между этими двумя вещами.
В учении о решении задач рассматриваются два типа планов (или операторов): алгоритмы и эвристические приемы. Они отличаются друг от друга наличием или отсутствием гарантии получения правильного результата. Алгоритм — это совокупность правил, которая если ей следовать автоматически порождает верное решение. Правила умножения представляют собой алгоритм; пользуясь ими надлежащим образом, мы всегда получим правильный ответ. Эвристические приёмы больше напоминают эмпирические правила: это процедуры или описания которыми относительно легко пользоваться и ценность которых оправдывается предшествующим опытом решения задач. 0днако в отличие от алгоритмов эвристические приёмы не гарантируют успеха. Для многих из числа наиболее сложных и наиболее интересных задач, алгоритмы решения не найдены, а в некоторых случаях даже известно, что они не существуют.
В таких случаях приходится прибегать к эвристическим приемам.
Эвристика вступает в действие во всякой сложной ситуации, связанной с решением задач. Большинство исследований, посвященных решению задач, в значительной мере сводится к изучению типов эвристических приемов, применяемых человеком.
Особенности рассмотренных стратегий решения задачи коренятся в общем характере процессов, протекающих в мозгу человека, и в их организации. Более того, эти общие организационные принципы, несомненно применимы к любым системам, которые хранят, отыскивают и используют информацию, будь то системы электронные или биологические. Ввиду этой общности при всякой попытке найти принципы устройства человеческого мозга целесообразно рассмотреть принципы организации самых разнообразных информационных систем. Подчеркиваем, речь идет именно о принципах, детали выполнения различных функций и механизмы их осуществления нас здесь не интересуют. Если мы умеем определить, что данная система использует эвристический прием сопоставления целей и средств, то не имеет значения, построена ли система из нейронов, интегральных схем или из рычагов и шестеренок, — эвристика во всех случаях одна.
О. К. Тихомиров ИНФОРМАЦИОННАЯ И
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 316; Нарушение авторских прав?; Мы поможем в написании вашей работы!