
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания для выполнения заданий 1 страница
|
|
|
|
Задание 11 – 20
Для решения задач 11 – 20 рекомендуется учебное пособие
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.
Ч.1. М.: Оникс 21 век. 2005. Гл. I –IV, стр.39 – 91.
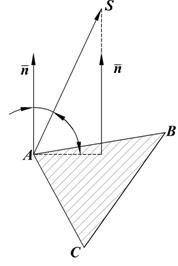
Рассмотрим решение аналогичной задачи, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).
1) Длину ребра АВ находим по формуле:

2) Угол между рёбрами 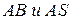 найдём по формуле косинуса угла между векторами
найдём по формуле косинуса угла между векторами 
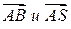 , координаты которых определяются так:
, координаты которых определяются так:
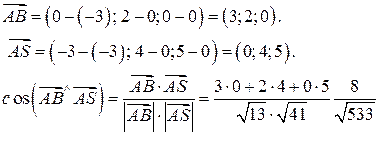



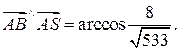
α
φ
Для решения задания 3) целесообразно решить задачу 7). Уравнение плоскости  составим по уравнению
составим по уравнению
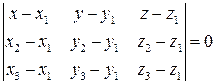
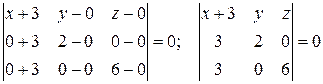

Нормальный вектор этой плоскости
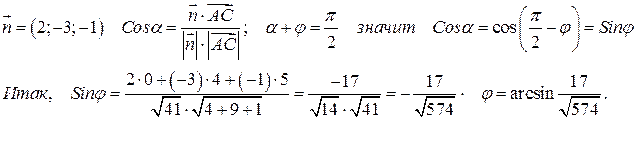
4) Площадь 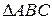 определяем с помощью векторного произведения:
определяем с помощью векторного произведения:
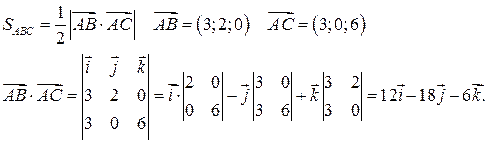
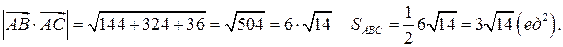
5) Объём пирамиды 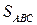 находится через вычисление смешанного произведения векторов
находится через вычисление смешанного произведения векторов 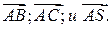 Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
6) Уравнение прямой 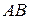
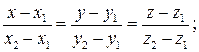
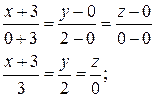
Канонические уравнения прямой, вектор  направляющий вектор прямой
направляющий вектор прямой 
8) Для определения проекции вершины 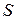 на плоскость
на плоскость  выполняются следующие действия:
выполняются следующие действия:
а) составляется уравнение высоты пирамиды 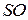 .
.
б) находится точка пересечения высоты и основания  решением системы, содержащей уравнение высоты и уравнение плоскости.
решением системы, содержащей уравнение высоты и уравнение плоскости.
Решение: вектор 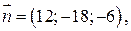 удобнее взять
удобнее взять 

Он будет направляющим для  По уравнению
По уравнению 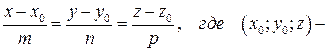
вершина 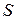 , т.е.
, т.е. 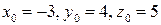
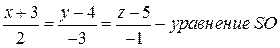 .
.
Система 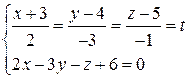 решается подстановкой
решается подстановкой

Подставив во второе уравнение, найдём значение 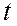 , а следовательно значения
, а следовательно значения

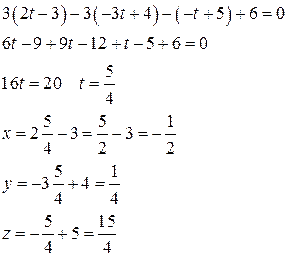
Точка 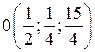 - проекция точки
- проекция точки 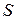 на плоскость
на плоскость 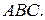
9) Длину высоты 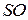 пирамиды можно найти по формуле
пирамиды можно найти по формуле 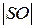 или по формуле расстояния от точки до плоскости – наиболее удобно.
или по формуле расстояния от точки до плоскости – наиболее удобно.
Изучите формулы самостоятельно, решив задание 9).
Задание 51 – 60
Дана система линейных уравнений
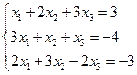
Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а) данной системе соответствует матричное уравнение 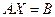 , которое решается по формуле:
, которое решается по формуле:  . Матрицы имеют вид:
. Матрицы имеют вид:

Находим обратную матрицу
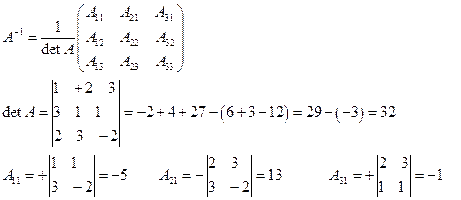
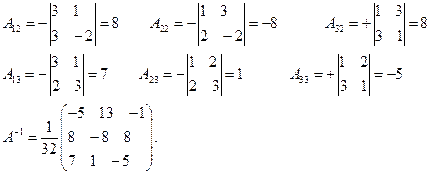
Находим матрицу 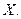

б)  - формулы Крамера. Вычислим все определители
- формулы Крамера. Вычислим все определители 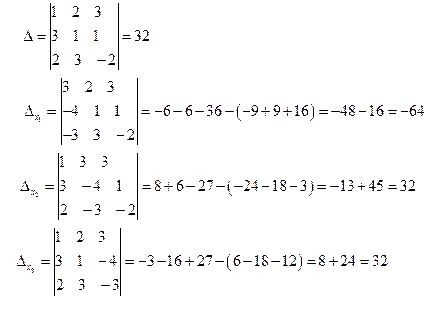
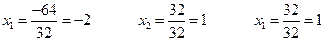
в) Метод Гаусса.
Составим расширенную матрицу 
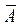 и преобразуем её с помощью элементарных преобразований.
и преобразуем её с помощью элементарных преобразований.
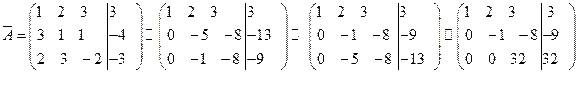
Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные  и
и 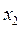 . Найдём
. Найдём  .
. 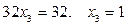 .
.
Вторая строка соответствует уравнению:
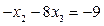 или
или 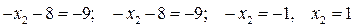
Аналогично из первой строки напишем уравнение:
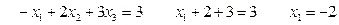
Итак: 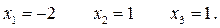
Задание 91 – 100.
Дано комплексное число 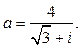
Записать число  в геометрической и тригонометрической формах и найти все корни уравнения
в геометрической и тригонометрической формах и найти все корни уравнения 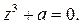
Рекомендуемая литература: Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.
Найдём алгебраическую форму комплексного числа
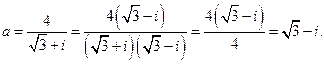
Тригонометрическая форма комплексного числа 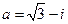 определится по формуле
определится по формуле 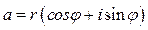 .
.
Изобразив число на плоскости, найдём 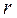 и
и  .
. 
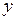



 -1
-1 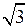
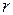


Итак, число 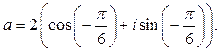
Найдём корни уравнения 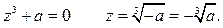
 вычислим по формуле Муавра
вычислим по формуле Муавра
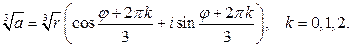
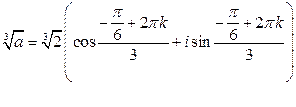

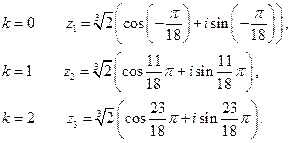
Задание 111 – 120
Вычислить пределы:
а) 
За скобку выносили наивысшую степень 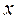 для числителя и знаменателя.
для числителя и знаменателя.
б) 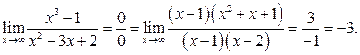
Для исключения неопределённости 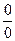 требуется числитель и знаменатель разложить на множители.
требуется числитель и знаменатель разложить на множители.
в) 

В данном случае для исключения неопределённости 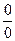 использованы эквивалентные бесконечно малые, например
использованы эквивалентные бесконечно малые, например 
 г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю
г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю
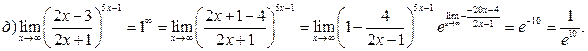
Задание 141– 150
Найти производные  следующих функций:
следующих функций:
а) 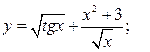 б)
б)  ;
;
в)  г)
г) 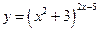 ;
;
д) 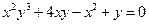 .
.
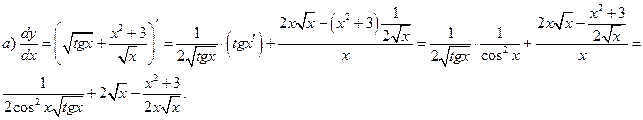
б) 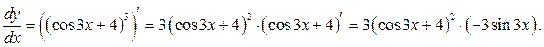
в) 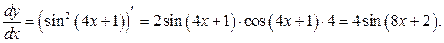
г) 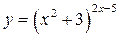
Прологарифмируем обе части равенства
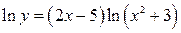
Продифференцируем обе части равенства
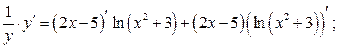
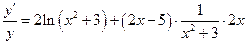

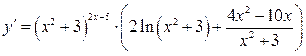
д) 
Функция 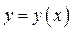 задана неявно. Учитываем, что
задана неявно. Учитываем, что 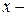 аргумент,
аргумент,  функция.
функция.
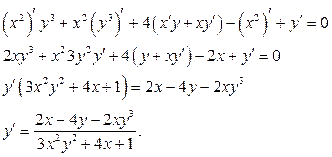
Задание 151 – 160
Найти 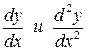 функций:
функций:
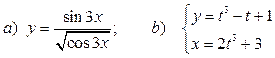
Решение:
а) 
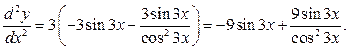
б) 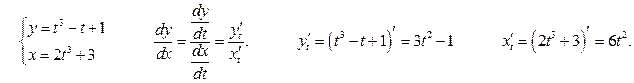
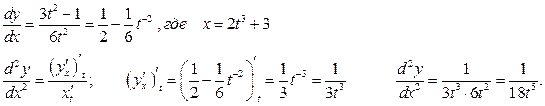
Задание 191 – 200
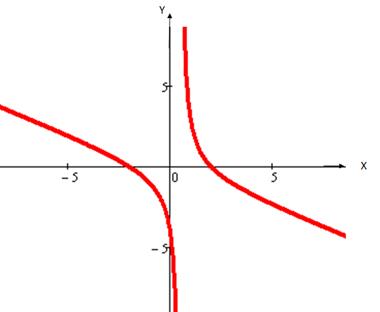
Исследовать методами дифференциального исчисления функцию и построить её график.
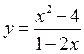
Рассмотрим свойства функции:
1. Область определения: 
2. Чётностьь, нечётность функции: 
Функция общего вида.
3. Асимптоты.
а) Так как 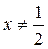 , то прямая
, то прямая 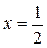 является вертикальной асимптотой:
является вертикальной асимптотой:

б)  – наклонная асимптота.
– наклонная асимптота.
Найдём 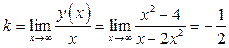
Найдём 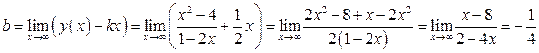
 – уравнение наклонной асимптоты.
– уравнение наклонной асимптоты.
4. Найдём точки экстремума и интервалы монотонности функции:


Так как 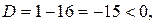 то действительных корней нет, значит, нет точек экстремума.
то действительных корней нет, значит, нет точек экстремума.
Производная 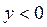 на всей области определения, значит функция
на всей области определения, значит функция
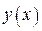 убывает.
убывает.
5. Точки пересечения с координатными осями
а) с осью  при
при 
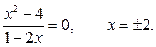 ,
,
б) с осью 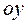 при
при 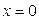
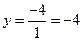 .
.
Используя исследование функции, строим график (схематично).
 Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.
Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.

Задание 231-240
Показать, что функция  удовлетворяет равенству:
удовлетворяет равенству:

Находим частные производные по 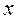 и по
и по 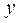 :
:


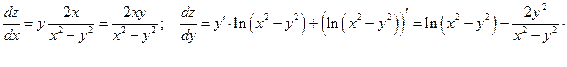 Подставим в равенство частные производные.
Подставим в равенство частные производные.
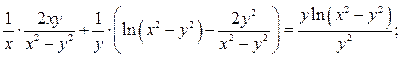
 ;
;

Равенство верно.
Задание 251-260
Найти наименьшее и наибольшее значения функции 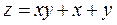
в области
 |
y








 В С
В С
D
А D
0 1 2 x
а) Найдём стационарные точки
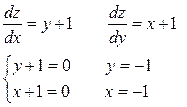
Точка 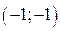 - стационарная, но не принадлежит области D.
- стационарная, но не принадлежит области D.
б) Исследуем данную функцию на границах квадрата АВСD
АВ:
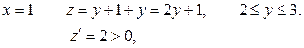
Функция возрастает на границе АВ 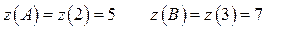
ВС: 
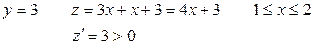
На границе ВС функция возрастает 

Значит на границе  фнкция возрастает
фнкция возрастает 

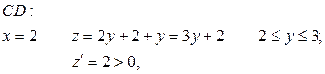
Значит на границе  фнкция возрастает
фнкция возрастает 
Найденные значения z сравним и выделяем
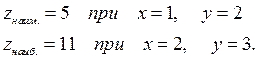
Задание 261 – 270
Дана функция 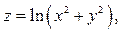 точка
точка 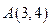 и вектор
и вектор 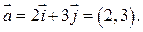
 Найти
Найти 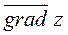 в точке
в точке  и производную в точке
и производную в точке  по направлению вектора
по направлению вектора 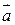 .
.
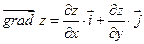
Найдём частные производные и вычислим их значение в точке  .
. 

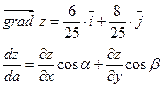
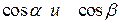 – направляющие косинусы вектора
– направляющие косинусы вектора 
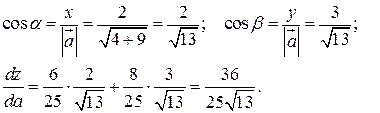
Литература к заданиям 231 – 240, 251 – 260, 261 – 270 – П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах
гл. VIII §§1-2, §4. 
Задание 281 – 290
Найти неопределённые интегралы, выполнив проверку дифференцированием в первых двух примерах.
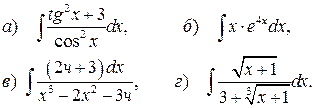
Решение:
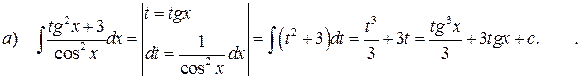
Проверка:

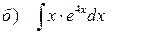
Метод интегрирования по частям для функции 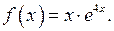
Формула: 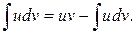
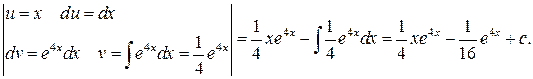
Проверка:
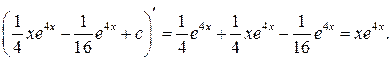
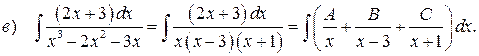
Найдём коэффициенты
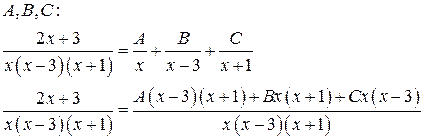
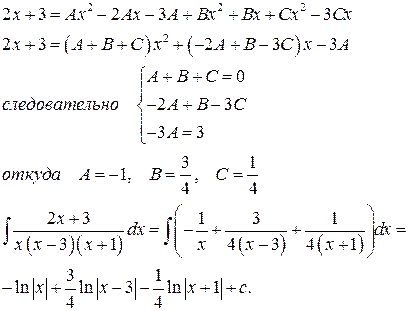
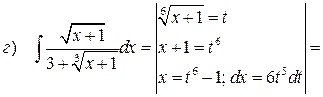

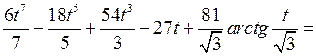
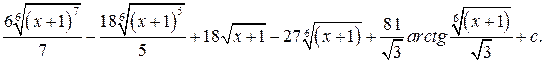
Задания 301– 310
Вычислить несобственный интеграл
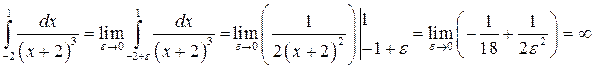
Несобственный интеграл расходится.
Методы интегрирования рассматриваются в учебном пособии П.Е. Данко,
А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах ч. I, гл. IХ. §§1-4.
Задание 321 – 330
В данном задании предлагается решить дифференциальное уравнение одного из трёх типов – однородное, линейное или с разделяющимися переменными. Предлагается решение однородного уравнения
Найти общее решение дифференциального уравнения первого порядка.

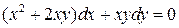 .
.
Уравнение является однородным.
Функции 
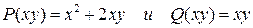 однородные второго порядка.
однородные второго порядка.
Уравнение можно привести к виду
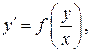 разделить обе части на
разделить обе части на  а затем на
а затем на 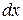 .
.
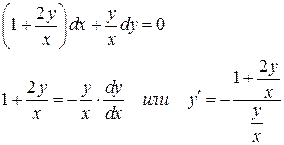
Введём подстановку

Разделяем переменные:
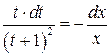
Интегрируем обе части, получаем

Общее решение примет вид
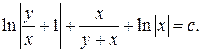
Задание 341-350
Найти общее и частное решения дифференциального уравнения
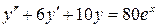 при начальных условиях
при начальных условиях 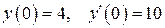 .
.
Однородное уравнение
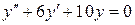 имеет характеристическое уравнение
имеет характеристическое уравнение 
корни которого  .
.
Тогда общее решение 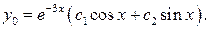
- для однородного уравнения
Согласно теории общее решение данного неоднородного уравнения имеет вид  частное решение данного уравнения, правя часть которого
частное решение данного уравнения, правя часть которого 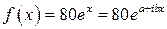
Учитывая стандартную формулу правой части, находим 
Число  не совпадает с
не совпадает с 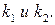
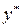 подбираем с учётом этого
подбираем с учётом этого 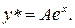
Найдём 
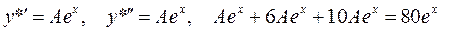

|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!