Основи термодинаміки

Термодинаміка вивчає теплові властивості макроскопічних систем, не звертаючись до мікроскопічної будови тіл, які входять в систему. Вона побудована на базі декількох основних принципів – законів (початків) термодинаміки, які є узагальненням численних відомих дослідних фактів, що відносить її до феноменологічних теорій фізики. При вивченні основ термодинаміки необхідно ввести декілька понять.

Термодинамічною системою називають сукупність тіл або частинок, які взаємодіють та обмінюються енергією як між собою, так і із зовнішнім середовищем. Зовнішнім середовищем називають сукупність тіл, які не входять у досліджувану термодинамічну систему. Замкнутою називається термодинамічна система, яка не обмінюється із зовнішнім середовищем ні енергією, ні речовиною. Термодинамічні параметри (параметри стану) – сукупність фізичних величин, які характеризують властивості термодинамічної системи (звичайно вибирають тиск, об'єм, температуру). Термодинаміка розглядає тільки рівноважні стани – такі, в яких параметри системи не змінюються зі спливанням часу.

Термодинамічним процесом називають будь-яку зміну в системі, пов'язану зі зміною хоча б одного із її термодинамічних параметрів. Процеси бувають оборотними і необоротними. Оборотним називають такий процес, який може бути проведений як у прямому, так і у зворотному напрямі через ту ж саму послідовність проміжних станів, після чого ні в самій системі, ні у навколишньому середовищі не відбувається ніяких змін. Такі процеси є фізичною абстракцією, ідеалізацією реальних процесів. Проте їхній розгляд є суттєвим з двох причин: по-перше, багато процесів у природі і техніці практично оборотні, по-друге, такі процеси є найекономічнішими, що дозволяє вказати шляхи підвищення коефіцієнтів корисної дії (ККД) реальних теплових двигунів (про що ми поговоримо нижче). Необоротним називають будь-який процес, що не задовольняє умові оборотності. Всі реальні процеси є необоротними, оскільки супроводжуються тертям або теплопередачею від гарячих тіл до холодних та неминучою при цьому дисипацією (розсіянням) енергії.

Основне поняття термодинаміки – внутрішня енергія системи U. Внутрішня енергія термодинамічної системи – це сумарна кінетична енергія хаотичного (теплового) руху частинок системи та потенціальна енергія взаємодії цих частинок. До внутрішньої енергії не відносяться кінетична енергія системи, як цілого, і потенціальна енергія системи у зовнішніх полях. Найважливіша властивість внутрішньої енергії – що вона є однозначною функцією стану системи, тобто у кожному стані система володіє цілком певним запасом внутрішньої енергії. Це означає, що при переході системи із одного стану в інший, зміна внутрішньої енергії D U визначається тільки різницею її значень U ₁ та U ₂ в цих станах, і не залежить від шляху переходу.

Ступенями свободи називаються незалежні координати, які повністю визначають положення тіла у просторі. Молекули одноатомного газу беруться за матеріальні точки, які не мають розмірів. Положення одноатомних молекул у просторі однозначно задається трьома координатами (x, у, z), оскільки вони можуть рухатись тільки поступально. Говорять, що такі молекули мають три ступеня свободи (і=3). Внаслідок хаотичності руху молекул, всі напрями руху рівноімовірні, тому кінетична енергія теплового руху таких молекул рівномірно розподілена між трьома ступенями свободи. Молекули двоатомного газу є двома атомами, жорстко зв'язаними між собою (мають форму гантелі). Такі молекули беруть участь і у поступальному, і у обертальному русі, тому вони характеризуються поступальними і обертальними ступенями свободи (кути повороту молекули навколо просторових осей служать такими ступенями свободи). Всього у двоатомних молекул п'ять ступенів свободи (і= 5, три поступальних та два обертальних, оскільки обертанням навколо третьої осі – осі самої молекули - нехтуємо).

Якщо молекули газу складаються із трьох та більше атомів (багатоатомні), зв'язаних жорсткими зв'язками, вони мають шість ступенів свободи (і=6, три поступальних і три обертальних). Якщо атоми зв'язані нежорсткими зв'язками, вони можуть коливатись навколо центру тяжіння і мають додатково коливальні ступені свободи. Наприклад, двоатомна нежорстка молекула має два коливальні ступені свободи – вона може коливатись уздовж осі молекули (всього у таких молекул три поступальних, два обертальних та два коливальних ступеня свободи). Чим складніша молекула, там більше у неї коливальних ступенів свободи, проте, для простоти, ми вважатимемо їх жорсткими, і коливаннями нехтуватимемо.

Больцман сформулював закон про рівномірний розподіл енергії молекул по їхніх ступенях свободи: для системи, що знаходиться у стані термодинамічної рівноваги, на кожен поступальний і обертальний ступені свободи доводиться в середньому кінетична енергія, рівна kT/ 2, а на кожен коливальний ступінь свободи – в середньому енергія, рівна kT. Коливальний ступінь свободи «володіє» удвічі більшою енергією тому, що на неї доводиться не тільки кінетична енергія (як у разі поступального і обертального руху), але і потенціальна, причому середні значення обох видів енергії однакові.

На минулій лекції нами одержана формула (5.24) для середньої кінетичної енергії поступального руху одноатомної молекули: e_сер =3 × (k×T/ 2), де множник «3» відносився до трьох поступальних ступенів свободи одноатомних молекул. Якщо ж до складу молекули входять два або більше атомів, то у загальному випадку її середня кінетична енергія визначається співвідношенням:

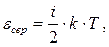(6.1)

де і= (і_пост+і_обер+ 2 і_колив) – загальна кількість ступенів свободи молекули. У ідеальному газі молекули не взаємодіють, тому їхня взаємна потенціальна енергія дорівнює нулю, а внутрішня енергія уявляє собою сумарну кінетичну енергію теплового руху всіх молекул. Внутрішня енергія одного моля ідеального газу становить:

(6.2)

оскільки k×N_A=R. Для довільної маси газу m, його внутрішня енергія визначається так:

(6.3)

де n - кількість молів речовини.

Внутрішню енергію системи можна змінювати двома способами.

1) Механічним способом, якщо енергія передається системі зовнішніми тілами. Наприклад, якщо в циліндрі із рухомим поршнем знаходиться ідеальний газ, то діючи на поршень зовнішньою силою і здійснюючи при цьому роботу, можна змінювати внутрішню енергію системи. Якщо газ стискається, його температура підвищується і внутрішня енергія зростає за рахунок здійснення поршнем механічної роботи. При розширенні газу його внутрішня енергія зменшується, перетворюючись на механічну енергію рухомого поршня.

2) За допомогою теплообміну – процесу передачі внутрішньої енергії без здійснення роботи. Якщо привести у зіткнення два тіла із різними температурами, то в результаті обміну енергіями температура гарячішого тіла буде знижуватись, а холоднішого – підвищуватись. При цьому кінетична енергія теплового руху молекул першого тіла переходить у кінетичну енергію теплового руху молекул другого тіла. Міра енергії, одержувана або віддавана тілами в процесі теплообміну, називається кількістю теплоти.

Таким чином, робота і теплота є двома формами передачі енергії від одних тіл до інших. Якщо внутрішня енергія, як ми відзначали вище, є однозначною функцією стану системи, то робота і теплота визначаються видом процесу переходу системи із одного стану у інший, тобто єфункціями процесу. Обчислимо елементарну роботу, здійснену ідеальним газом при його розширенні. Нехай в циліндрі під поршнем площею S знаходиться газ, який займає об'єм V під тиском р. Газ тисне на поршень силою F=p×S, і при переміщенні його на відстань dl, здій-

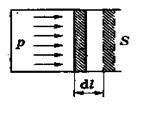Рис.6.1.

снює роботу (рис.6.1): (6.4) де S×dl=dV –зміна об'єму газу. Якщо dV>0 (газ розширюєть-ся), то dА>0 – робота додатна. Якщо газ стискається, то dV < 0, тому dА < 0 – роботу газу вважають від¢ємною. Повну

роботу, здійснювану газом при зміні його об'єму від V₁ до V₂, обчислюють інтегруванням:

(6.5)

Визначимо роботу, здійснювану газом при різних ізопроцесах.

1) При ізохорному процесі V=const, а отже dV= 0, тому A= 0.

2) При ізобарному процесі р=const, тоді

(6.6)

(Останнє виходить із рівняння стану ідеального газу).

3) При ізотермічному процесі Т=const. Виразивши тиск із рівняння стану ідеального газу p=m×R×T/M×V і підставивши, отримаємо:

(6.7)

(Останнє виходить із закону Бойля-Маріотта: p ₁ ×V ₁ =p ₂ ×V ₂).

При наданні системі елементарної кількості теплоти dQ, її температура зросте при цьому на dT. Теплоємністю С системи називають кількість теплоти, потрібну для підвищення її температури на один Кельвін:

(6.8)

Одиниця виміру теплоємності – Джоуль на Кельвін (Дж/К). Розрізняють питому та молярну теплоємності. Питома – це теплоємність одиниці маси речовини:

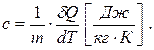(6.9)

Молярна - це теплоємність одного моля речовини:

(6.10)

Очевидно, що питома і молярна теплоємності зв'язані формулою:

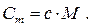(6.11)

Знаючи питому або молярну теплоємності, можна визначити кількість теплоти, одержану системою:

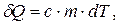або (6.12)

Як згадувалось вище, основу термодинаміки складають два закони (або початку). Історично для формулювання першого початку важливу роль зіграли невдалі спроби людини створити вічний двигун першого роду - періодично діючу машину, яка здійснювала б роботу, більшу за передану їй ззовні енергію. Перший закон термодинаміки формулюється так: неможливо створити вічний двигун першого роду. Цей закон є законом збереження і перетворення енергії: при різноманітних процесах, які протікають в природі, енергія не виникає із нічого і не знищується, а лише перетворюється з одного виду в іншій.

Щоб записати цей закон в математичній формі, розглянемо процес зміни внутрішньої енергії. У загальному випадку внутрішня енергія може змінюватись як в результаті здійснення роботи зовнішніми тілами, так і внаслідок теплообміну. При обміні енергією із навколишніми тілами залежно від обставин вона може як зростати, так і зменшуватись: знак dQ указує напрям теплообміну. Якщо при теплообміні навколишні тіла відбирають тепло у даного тіла і нагріваються, то dQ<0. Якщо дане тіло здійснює роботу над зовнішніми тілами за рахунок зміни внутрішньої енергії, ця робота вважається додатною. Якщо ж навколишні тіла здійснюють роботу над даним тілом, то ця робота від¢ємна. Враховуючи правило знаків, закон збереження енергії стосовно до процесу зміни внутрішньої енергії системи, що відбувається, можна сформулювати так: зміна внутрішньої енергії системи дорівнює сумі одержаної системою кількості тепла і здійсненої над нею роботи:

dU=dQ-dА. (6.13)

або кількість одержаного системою тепла іде на збільшення його внутрішньої енергії і на здійснення нею роботи над зовнішніми тілами:

dQ=dU+dА. (6.14)

Так формулюється перший початок термодинаміки – закон збереження енергії стосовно теплових процесів. У цьому виразі dU є повним диференціалом, а dQ та dА такими не є. У інтегральному вигляді перший закон термодинаміки має вигляд: Q= D U+A. Оскільки при роботі теплового двигуна система періодично повертається у початковий стан, то при цьому зміна її внутрішньої енергії D U=0. Тому, згідно першому початку термодинаміки, A=Q, що і підтверджує тезу про неможливість створення теплового двигуна першого роду.

Застосуємо цей закон до різних ізопроцесів.

1) Ізохорний процес. Розглянемо ізохорне нагрівання 1 моля газу. Оскільки V=const, то dV=0, а отже, dA=p×dV=0. Тому перший початок термодинаміки набуває вигляду: dQ=dU, тобто вся теплота, надана газу при ізохорному процесі, іде тільки на збільшення його внутрішньої енергії. Підставивши в цей вираз величину dQ через значення молярної теплоємності С_V для ізохорного процесу та величину зміни внутрішньої енергії, матимемо:

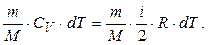(6.15)

Звідси одержуємо вираз молярної теплоємності ізохорного процесу:

(6.16)

Оскільки розглядається ідеальний газ, то С_V від температури не залежить і є постійною величиною.

2) Ізобарний процес. При р=const змінюються і об'єм, і температура газу, а отже, системою здійснюється робота dА=р×dV, та змінюється її внутрішня енергія dU. При ізобарному процесі dQ_p=C_p×dT, тому перший початок термодинаміки для одного моля газу має вигляд:

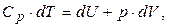(6.17)

або, оскільки внутрішня енергія є функцією тільки температури, то dU=C_V×dT, отже:

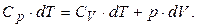(6.18)

Для одного моля газу рівняння стану має вигляд: p×V=R×T. Продиференціювавши його при р=const маємо:

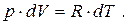(6.19)

Підставивши у вираз першого закону термодинаміки (6.18), отримаємо:

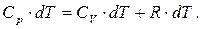(6.20)

Звідси одержимо співвідношення між молярними теплоємностями ізобарного та ізохорного процесів – рівняння Майєра:

(6.21)

Очевидно, що С_р завжди більша за С_V на величину молярної газової сталої R. Це пояснюється тим, що при ізобарному нагріванні газу потрібна ще додаткова кількість теплоти на здійснення роботи розширення газу, оскільки постійний тиск забезпечується збільшенням об'єму газу. Підставивши в це рівняння значення С_V, одержимо вираз для молярної теплоємності ізобарного процесу:

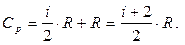(6.22)

3) Ізотермічний процес. При Т=const внутрішня енергія не змінюється, тому dU= 0, і перший закон термодинаміки набуде вигляду: dQ=dА, тобто, вся теплота, надана газу при ізотермічному процесі, іде тільки на здійснення ним роботи проти зовнішніх сил. Молярна теплоємність цього процесу С_Т ®¥, оскільки теплота, яка підводиться, не приводить до збільшення температури системи.

Адіабатним називається процес, що протікає без теплообміну між системою та навколишнім середовищем (dQ= 0). Здійснити цей процес можна у випадку, якщо газ знаходиться усередині оболонки з ідеальними теплоізоляційними властивостями. Оскільки на практиці повна теплоізоляція нездійсненна, та умова dQ= 0 виконується приблизно для швидкоплинних процесів. Прикладом такого процесу може служити вибух горючої суміші при роботі двигуна внутрішнього згоряння. Перший закон термодинаміки для адіабатного процесу має вигляд: 0 = =dU+dА, звідки dA=-dU, тобто при адіабатному розширенні газ здійснює роботу за рахунок зменшення своєї внутрішньої енергії – його температура при цьому знижується. Явище охолоджування газу при адіабатному розширенні широко використовується в техніці, наприклад в роботі холодильних установок. Якщо ж перший закон термодинаміки записати у вигляді - dA=dU, то його формулювання звучить так: при адіабатному стисненні робота зовнішніх сил іде на збільшення внутрішньої енергії газу, тобто температура його при цьому зростає.

Рівняння адіабатного процесу носить назву рівняння Пуассона, яке має вигляд: p×V^g=const, де g=C_p/C_V – показник адіабати (коефіцієнт Пуассона). Згідно рівнянню Майєра, C_p > C_V, отже, g >1. Тому, адіабата в координатах p-V іде крутіше, ніж ізотерма, рівняння якої p×V ¹ = const (рис. 6.2). Це можна пояснити тим, що

	при адіабатному розширенні газ охолоджується, і зменшення тиску обумовлене не тільки збільшенням об'єму (як при ізотермічному процесі), але і зменшенням температури. Значення показника адіабати залежить від структури молекул газу – від числа їхніх ступенів свободи: (6.23)
Рис.6.2.

Для одноатомних газів і= 3, g= 1,67; для двоатомних - і= 5, g= 1,4; для трьох- і більше атомних (або багатоатомних) і= 6, g= 1,33. Робота, здійснювана ідеальним газом при адіабатному розширенні, визначається формулою:

(6.24)

Виразивши із рівняння Майєра значення С_V=R/ (g- 1) і підставивши, формулу для роботи можна переписати у такому вигляді:

(6.25)

Робота, здійснювана газом при адіабатному процесі менша, ніж при ізотермічному, оскільки при адіабатному розширенні відбувається охолодження газу, тоді як при ізотермічному температура підтримується сталою за рахунок притоку ззовні еквівалентної кількості тепла.

У термодинаміці важливе значення мають такі процеси, коли система, прой-шовши через ряд проміжних станів, повертається у початковий стан. Такі замкнуті (кругові) процеси називають циклами. Якщо система повертається до початкових значень своїх параметрів, то говорять, що дана система здійснює цикл. На діа-грамах станів цикли зображуються замкнутими кривими. Будь-який цикл складається із двох процесів: процесу розширення системи та процесу її стиснення. Робота розширення додатна, а стиснення – від¢ємна, тому сумарна робота системи

Рис.6.3.

за цикл визначається його площею і дорівнює алгебраїчній сумі обох робіт: А=А 1 -А 2. Цикл, за який здійснюється додатна робота А > 0, (якщо робота розширення А 1 більша за роботу стиснення А 2) протікає за годинниковою стрілкою і називається прямим (рис. 6.3). А цикл, за який здійснюється від‘ємна робота А < 0, (у якому робота розширення А 1 менша за роботу стиснення А 2) протікає проти годинникової стрілки і називається зворотним (рис.6.4). Прямі цикли використовуються у теплових двигунах – періодично діючих машинах, які здійснюють роботу за рахунок одержаної зовні теплоти. Зворотні цикли використовуються у холодильних машинах - періодично діючих установках, в яких за рахунок роботи зовнішніх сил теплота відбирається від менш нагрітих тіл і передається більш нагрітим. Тепловий двигун є пристроєм, який періодично перетворює внутріш-

Рис.6.4.

ню енергію палива у механічну. Енергія, що виділяється при згорянні палива, шляхом теплообміну передається робочому тілу – термодинамічній системі (газу), яка здійснює процес перетворення однієї форми енергії в іншій. Розширюючись, газ здійснює роботу проти зовнішніх сил, приводячи в рух механізм. Будь-який вид енергії може бути повністю перетворений в теплоту, проте внутрішню енергію системи не можна вичерпати повністю і перетворити на інший вид енергії, оскільки хаотичний рух молекул є природним станом речовини. Будь-який тепловий двигун складається і з трьох основних частин: робочого тіла, нагрівача і хо-

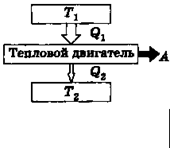Рис.6.5.

лодильника (охолоджувача). Від нагрівача – термостата із більш високою температурою Т 1– робоче тіло (газ або пара) одержує деяку кількість теплоти Q 1і при розширенні здійснює корисну роботу А 1(рис.6.5). Температура нагрівача Т 1 залишається сталою за рахунок згоряння палива. Оскільки тепловий двигун повинен працювати циклічно, для отримання виграшу в роботі за цикл А, робота стиснення А 2мусить бути меншою за роботу розширення. То-му при стисненні робочому тілу треба передати деяку кіль-

кість теплоти Q ₂ холодильнику, якиймає нижчу температуру Т ₂, ніж нагрівач. Після закінчення циклу, робоче тіло повертається в свій початковий стан, а його внутрішня енергія набуває початкового значення. Тому робота циклу може здійснюватись тільки за рахунок зовнішніх джерел, що підводять тепло до робочого тіла. (Реальні теплові двигуни працюють по розімкненому циклу: після розширення газ викидається, а в машину вводиться і стискається нова порція газу).

Термічним коефіцієнтом корисної дії (ККД) теплового двигуна називають величину h, яка характеризує його ефективність, і визначувана відношенням корисної роботи, здійсненої за цикл, до витраченої кількості теплоти:

(6.26)

Часто ККД двигунів виражають у відсотках, помножуючи h на 100%.

У холодильній машині здійснюється зворотний цикл. Робочим тілом за цикл від холодильника (термостата із нижчою температурою Т ₂) віднімається кількість теплоти Q ₂та віддається нагрівачу (термостату із вищою температурою Т₁) кількість теплоти Q ₁ (рис.6.6). Для кругового процесу D U= 0, тому Q=A. Проте,

Рис.6.6.

кількість одержаної системою теплоти Q=-Q 2 -Q 1<0, тому A< 0і Q 2 -Q 1 =-A або Q 1 =Q 2 +A. Це означає, що кількість теплоти Q 1, віддана системою нагрівачу, більша за кількість теплоти Q 2, одержаного від холодильника, на величину роботи А, здійсненої над системою. Холодильний коефіцієнт характеризує ефективність холодильної машини і визначається відношенням теплоти, що відніме у холодильника, до роботи, що витрачається на приведення її в дію:

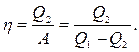(6.27)

Розглядаючи питання про ККД теплових машин, Карно показав, що максимальний ККД можна одержати при оборотному круговому процесі, який складає-

	ться із двох рівноважних ізотермічних і двох рівноважних адіабатних процесів (рис.6.7), які чергуються між собою. Неважко довести, що ККД ідеального циклу Карно з ідеальним газом, як робочим тілом, залежить тільки від температур нагрівача і холодильника: (6.28)
Рис.6.7.

Висловлюючи закон збереження та перетворення енергії, перший закон тер-модинаміки не дозволяє встановити напрямок протікання термодинамічних процесів. Крім того, існує безліч процесів, які не суперечать першому початку, у яких енергія зберігається, але в природі вони не здійснюються. Поява другого початку (закону) термодинаміки пов'язана із необхідністю відповісти на питання: які процеси в природі можливі, а які ні? Другий початок термодинаміки визначає напрям протікання термодинамічних процесів у природі, пов'язаних із перетворенням енергії.

Перетворення теплоти в роботу можливе тільки за наявності нагрівача і холодильника: у всіх теплових машинах корисно можна використовувати тільки частину енергії, одержаної від нагрівача. Іншими словами, жоден тепловий двигун не може мати ККД, рівний одиниці. Існує декілька формулювань другого початку.

1) С.Карно: ККД ідеальної теплової машини визначається тільки температурами нагрівача і холодильника, і не залежить ні від конструкції машини, ні від типу робочого тіла.

2) Кельвина-Планка: неможливий круговий процес, єдиним результатом якого є перетворення теплоти, одержаної від нагрівача, повністю в роботу.

3) Р.Клаузіуса: неможливий круговий процес, єдиним результатом якого є передача теплоти від менш нагрітого тіла до більш нагрітого.

Другий початок термодинаміки заперечує можливість використання внутрішньої енергії якого-небудь джерела без переводу її на нижчий температурний рівень, тобто без холодильника. Періодично діючий двигун, який здійснює роботу за рахунок одного джерела теплоти, називається вічним двигуном другого роду. Тому, ще одним формулюванням другого початку термодинаміки можна вважати твердження: вічний двигун другого роду (працюючий тільки за рахунок охолодження нагрівача) неможливий.

Якісна відмінність теплового руху молекул від інших форм руху – його безладність, хаотичність. Тому для опису теплового руху вводять кількісну міру ступеня молекулярного безладу. Приведеною кількістю теплоти називається відношення кількості теплоти, одержаної тілом в ізотермічному процесі, до температури тепловіддаючого тіла Q/T. Приведена кількість теплоти, надана системі на нескінченно малій ділянці процесу, визначається як dQ/T. Алгебраїчна сума приведеної кількості теплоти для будь-якого оборотного кругового процесу дорівнює нулю:

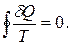(6.29)

Одержаний результат означає, що цей інтеграл не залежить від шляху інтегрування (від послідовності проміжних станів), тобто підінтегральний вираз є повним диференціалом деякої функції, якавизначається тільки станом системи і не залежить від шляху, яким система прийшла до цього стану (тобто, не є функцією процесу). Ця функція, що характеризує напрям протікання самодовільних процесів у замкнутій термодинамічній системі, називається ентропією. Тому:

(6.30)

Одиниця виміру ентропії – Джоуль на Кельвін (Дж/К). Отже, кожному стану системи відповідає одне певне значення ентропії. Тому ентропія і є однозначною функцією стану. Якщо система оборотним довільним шляхом переходить зі стану А у стан В, то одержана нею при цьому приведена кількість теплоти визначається так:

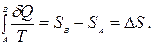(6.31)

Приведена кількість теплоти і межі інтегрування визначаються параметрами досліджуваного процесу. Із цієї формули виходить, що ентропія визначається із точністю до адитивної сталої, і фізичний зміст має не сама ентропія, а різниця ентропії (важливими є тільки зміни станів). Якщо система здійснює оборотний адіабатний процес, то при цьому dQ= 0, тому D S= 0, отже, S= const, тобто адіабатний процес протікає при незмінній ентропії. Якщо в замкнутій системі відбувається необоротний процес, то для нього справедлива нерівність:

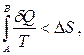(6.32)

тому D S=S_B-S_A> 0, таким чином S_B>S_A. Для необоротних процесів, як показують теорія та досвід, ентропія завжди зростає. Енергія замкнутих систем зберігається, тому при будь-яких змінах усередині них енергія на початку і в кінці процесу одна і та ж, і по значенню енергії не можна відрізнити початковий стан від кінцевого. Але по значенню ентропії можна судити про можливий напрям процесу (тобто, який стан є початковим, а який – кінцевим), оскільки у природно протікаючих процесах ентропія може тільки зростати.

В узагальненому вигляді, для довільних процесів справедлива нерівність Клаузіуса: D S ³0– ентропія замкнутих систем може або зростати (у разі необоротних процесів), або залишатися сталою (у разі оборотних). Це твердження відноситься тільки до замкнутих систем. Якщо система обмінюється теплотою із зовнішнім середовищем, то її ентропія може поводитись довільним чином.

Зв'язок ентропії із термодинамічною вірогідністю встановив Больцман: ен-тропія пропорційна логарифму термодинамічної вірогідності:

(6.33)

де k - стала Больцмана, W - термодинамічна вірогідність – кількість мікростанів (мікророзподілів), якими може бути реалізований даний макростан (або кількість способів, які реалізовують даний стан макроскопічної системи). Таким чином, ентропія – міра вірогідності стану термодинамічної системи. Статистичний зміст поняття ентропії полягає у тому, що збільшення ентропії ізольованої системи пов'язане з переходом цієї системи із менш вірогідних станів у більш вірогідні. Насправді, чим більша кількість мікростанів, які реалізовують даний макростан, тим більша його ентропія.

Одним із формулювань другого початку термодинаміки, що встановлює його статистичний характер, є формулювання Больцмана: всі процеси в природі про-тікають у напрямі від менш вірогідних до більш вірогідних. Необоротні процеси протікають самодовільно доти, доки система не досягне стану рівноваги, який відповідає максимальній вірогідності (ентропія при цьому досягає свого максимуму). Наприклад, перемішування двох газів при дифузії або вирівнювання температур двох газів із різними початковими температурами відбувається тому, що рівномірний розподіл молекул і температури по всьому об'єму статистично буде найвірогіднішим та відповідає максимальному значенню ентропії. Будучи статистичним законом, другий початок термодинаміки виконується для замкнутих систем, які складаються із великого числа частинок. Проте для термодинамічних систем, що складаються із нескінченного числа частинок, другий початок термодинаміки непридатний, оскільки для таких систем всі стани рівноімовірні.

ТЕСТОВІ ЗАВДАННЯ З РОЗДІЛУ “ОСНОВи МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ”

Дата добавления: 2014-11-07