Шешімді іздеу баптамасы

Поиск решения(Шешімін табу) – оптимизациялау есептерін шешуге арналған Excel қондырмасы. Егер Сервис менюінде Поиск решения командасы болмаса, онда оны жүктеу қажет. Ол үшін Сервис→Надстройки командасын ашып, Поиск решения қондырмасын белсенді ету керек. Егер Поиск решения Надстройки сұхбат терезенде болмаса, Windows-ң басқару панеліндегі Установка и удаление программ пиктограммасына шертіп, Excel (немесе Office) орнату программасының көмегімен Поиск решения қондырмасын орнату керек.

Поиск решения 5.1 суреттегі сұхбат терезесінің элементтерін қарастырайық.

Установить целевую ячейку(Мақсатты ұяшықты орнату) өрісіне максимумы, минимумы немесе берілген мән табылатын функция ұяшығына сілтеме жасалады. Шешім мен мақсатты ұяшық арасындағы өзара байланыстың типі Равной(Тең болатын) тобындағы ауыстырғыштарға белгі қою арқылы орнатылады. Мысалы, мақсатты функцияның максимумын немесе минимумын табу үшін ауыстырғыш Максимальному значению немесе Минимальному значению жағдайына сәйкесінше қойылады. Мақсатты функцияның берілген мәнін табу үшін Равной тобындағы Значению жағдайы таңдалады.

Изменяя ячейки(өзгеретін ұяшықтар) өрісіне есептің шешімін табу барысында өзгеруі қажет ұяшықтар адресі, яғни айнымалыларға бөлінген ұяшықтар көрсетіледі.

5.1-сурет – Поиск решения терезесі

Есептің айнымалыларына қойылатын шарттар Ограничения(Шектеулер) өрісінде бейнеленеді. Шешімін табу құралы теңдік, теңсіздік, сонымен қатар айнымалылардың бүтін сан болу шарты түріндегі шектеулерді енгізуге мүмкіндік береді. Шектеулер біртіндеп енгізіледі. Шектеулерді енгізу үшін Поиск решения сұхбат терезесіндегі Добавить батырмасына басу қажет және ашылған Добавление ограничения (Шектеулерді енгізу) 5.2 с уретте көрсетілген сұхбат терезесінің өрістерін толтыру керек.

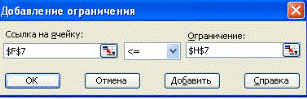
5.2-сурет – Шектеулерді енгізу терезесі

Ссылка на ячейкус(Ұяшыққа сілтеме) өрісіне шектеудің (шарттың) сол жағы, Ограничение(Шектеулер) өрісіне оң жағы енгізіледі. Ашылатын мына тізім арқылы шектеудің сол жағы мен оң жағының арақатысы таңдалады. Келесі шектеулерді енгізу үшін Добавление ограничения сұхбат терезесіндегі Добавить батырмасына басу қажет. Барлық шектеулер енгізілгеннен кейін ОК батыршамасы шертіледі.

Поиск решения сұхбат терезесінің Параметры батырмасы шешімді табу үшін қандай параметрлер берілгендігін текеру мақсатына қолданылады.

Параметры поиска решения сұхбат терезесінде зерттелетін мәселенің шешімін табудың варианттары мен шарттарын өзгертуге, сондай-ақ тиімді модельді жүктеуге және сақтауға болады. Үнсіз келісім бойынша қолданылатын басқару элементтерінің жағдайлары мен мәндері көптеген есептердің шешімі үшін жарайды.

Параметры поиска решения сұхбат терезесінің элементтерін арастырайық:

- Максимальное время өрісі есептің шешімін табуға кететін уақытты шектеу үшін арналған.

- Предельное число итераций өрісі аралық есептеулер санын шектеу үшін қажет.

- Относительная погрешность және Допустимое отклонение өрістері шешімнің қандай дәлдікпен табылатындығын анықтау үшін арналған. Үнсіз келісім бойынша берілген параметрлер арқылы табылған шешімді үлкен дәлдікпен және аз ауытқумен қайта тауып, сосын бастапқы шешіммен салыстырған орынды.

Мұндай тексеруді айнымалыларына бүтін сандық шарты қойылған есептерге жүргізу ұсынылады.

- Линейная модель жалаушасы сызықтық оптимизациялау есептерінің шешімін табу немесе сызықтық емес септердің сызықтық аппроксимациясы үшін қызмет етеді. Сызықтық емес есептер жағдайында бұл жалауша алынып тасталуы, ал сызықтық есеп жағдайында салынуы қажет, себебі кері жағдайда бұрыс шешім алынуы мүмкін.

- Показывать результаты итераций жалаушасы шешім табуды тоқтата тұруға және жекелеген итерациялардың нәтижелерін қарау үшін арналған.

- Автоматическое масштабирование жалаушасы өлшемі бойынша сапалық тұрғыда ерекшеленетін кіріс және шығыс мәндерді автоматты түрде нормализациялау үшін арналған, мысалы миллион теңгемен есептелетін салымдарға қатысты пайда пайызын максимизациялау жағдайында.

- Оценка тобы экстрополяция әдісін таңдау үшін қызмет етеді.

- Производные тобы сандық дифференциациялау әдісін таңдау үшін арналған.

- Метод тобы оптимизациялау алгоритмін таңдау үшін арналған.

Есептің шешімінің нәтижелері туралы есеп беруді дайындау үшін Результаты поиска решения сұхбат терезесінде қажетті есеп беру типін таңдау қажет: Результаты, Устойчивость, Пределы.

5.2 Тақырып бойынша тапсырмалар

1-тапсырма. Бояу өндірісін жоспарлау

Келесі өндірісті жоспарлауесебін қарастырайық. Кіші фабрика 2 түрлі: ішкі (І) және сыртқы (Е) жұмыстар үшін бояу шығарысымен айналысады.

Екі түрлі өнім көтерме саудаға түседі. Бояларды өндіру үшін екі бастапқы өнімдер А және В пайдаланылады. Тәуліктік максималды қоры 6 және 8 тонна құрайды. А және В өнімдерінің сәйкесінше бояулардың бір тоннаға шығындары 5.1 кестеге келтірілген.

5.1-кесте– Бояу өндірісін жоспарлау есебінің бастапқы мәндері

Бастапқы өнім	Бір тонна бояуға бастапқы өнім шығыны, т	Максималды мүмкін қор, т
Е бояуы	I бояуы
А
B

Өткізу нарығын зерттеуі І бояуының тәуліктік сұранысы Е бояуынан ешқашан 1 тоннаға артық болмағанын көрсетті. Осыған қоса, І бояуына деген сұраныс күніне 2 тоннадан артық емес екенін көрсетті. Бояулардың көтерме сауда бағалары: Е бояуы үшін 3000 тенге және І бояуы үшін 2000 тенге. Өнімді ақшаға айналдырудың табысы максималды болуы үшін фабрика әр бояудың қандай мөлшерін өндіру керек?

Осы есепті шығару үшін математикалық моделін құру керек. Моделді құру процессін бастау үшін келесі үш сұраққа жауап беру керек:

– модел қандай шамаларды анықтауға құрылады (яғни айнымалы моделдер);

– мүмкін болатын айнымалы шамалардың көбінен тиімдіні таңдау мақсаты неден құрылады;

– белгісіздер қандай шектерден аспауы керек.

Біздің жағдайымызда табысты барынша көп алу үшін фабрика дұрыс өндіріс көлемін жоспарлау керек. Осыған сәйкес айнымалылар: х_І І бояуының тәуліктік өндіріс көлемі және х_Е Е бояуының тәуліктік өдіріс көлемі.

Тәуліктік табыс жиынтығы z І бояуының өндірістік х_І және Е бояуының х₂ z=3000х₁+2000х_Е тең болады. Мүмкін болатын х_Е және х_І шамалардың ішінен фабрика мақсаты табыс жиынтығын максималданатын, яғни мақсатты z функциясын анықтау.

Енді х₁ және х_Е қойылатын шектерге көшейік. Бояларды өндіру көлемі теріс бола алмайды, яғни х₁, х_Е >= 0

Бояулардың екі түрін өндіруге қажетті бастапқы өнім шығыны мүмкін болатын бұл бастапқы өнім қорынан артық бола алмайды. Яғни,

,

.

Осыған қоса, бояуға деген сұраныс шамасының шегі:

,

.

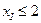Осылай, бұл есептің математикалық моделі келесі түрге ие:

Төменгі шек арқылы z=3000х₁+2000х_Е максималдау:

,

,

,

,

.

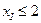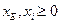Мұндағы модель сызықтық екенін ұмытпау керек, себебі мақсатты функция және шектер айнымалылардан сызықты байланыста тұр.

Бұл есепті Сервис, Шешім іздеу (Поиск решения) командасы арқылы шешейік. Шешім іздеу құралы Excel қондырғысының біреуі болып табылады. Егер Сервис менюінде Шешім іздеу командасы жоқ болса, онда оны құру үшін Сервис, Надстройки, Шешім іздеу командасын орындау қажет.

5.3 суретте көрсетілгендей A3 және ВЗ ұяшықтарын мен айнымалылар шамасына бөлейік.

5.3-сурет – Айнымалыларға, мақсатты функцияға және шектерге бөлінген диапазондар.

С4 ұяшығына мақсатты функцияны енгізейік

=3000*АЗ+2000*ВЗ.

А7:А10 ұяшықтарына сол жақ шектерді енгізейік

=АЗ+2*ВЗ;

=2*АЗ+ВЗ;

=ВЗ-АЗ;

=ВЗ,

В7:В10 ұяшықтарыдна – шектеулердің оң бөліктері.

Содан кейін Сервис, Шешім іздеу командасын таңдап, 5.4 суретте көрсетілген ашылған Шешім іздеу терезесін толтырамыз.

5.4-сурет – Бояу өндірісін жоспарлау есебінің Шешім іздеу терезесі.

5.5 суретте көрсетілген Орындау батырмасын басқаннан кейін Шешім іздеу нәтижелері атты терезе ашылады да, шешім табылды деген ақпаратты береді.

5.5-сурет– Шешім іздеу нәтижесінің терезесі.

Бұл есептің нәтиже санаулары (өндірістің тиімді жоспары мен оған сәйкес табыс) 5.6 суретте көрсетілген. Ең тиімді болып күніне Е бояуының 3,33 т және І бояуының 1,33 т өндірісі табылады..Бұл өндіріс көлемі фабрикаға 12,67 мың. тенге табыс әкеледі.

5.6-сурет– Бояу өндірісін жоспарлау есебінің шешім іздеу құралы көмегімен есептелген нәтиже санаулары.

2-тапсырма. Қорытпалардың құрамын анықтау

Есепті қарап шығайық: А және В қорытпалар алу үшін І, ІІ, ІІІ және ІV металлдар қолданылады. Олардың А және В қорытпалардың құрамында болу талаптары 5.2 кестеде келтірілген.

І, ІІ, ІІІ және ІV металлдарын өндіруге қажетті кендер қорлары мен олардың мінездемелері 5.3 кестеде көрсетілген.

5.2-кесте – Қорытпа құрамын анықтау есебіндегі металлдардың қорытпа құрамында болу талаптары.

Қорытпа	Металл құрамына қойылатын талаптар
А	I металлының 80 %-нен артық емес
II металлының 30 %-нен артық емес
В	II металының 40 %-нен 60 %-не дейін
III металлының 30 %-нен кем емес
IV металлының 70 %-нен артық емес

5.3 Кесте– Қорытпа құрамын анықтау есебіндегі кендер мінездемесі мен қоры

Кен	Максималды қор, т	Құрамы, %	Баға, доллар
I	II	III	IV	басқа компоненттер

А қорытпасының 1 т бағасы 200 долларов болсын, ал В қорытпасының 1 т – 210 доллар. А және В қорытпаларын сатқаннан келген пайданы максималдау қажет..

А және В қорытпаларын алуға қажетті І, ІІ, ІІІ және ІV металлдарының санын сәйкесінше 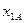, , 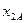, и 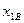, , 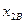, 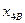белгілейік. Қолданылған -нші кен санын деп белгілейік.

Осылай, бұл есептің математикалық моделі келесі түрге ие:

максималдау:

Қорытпа құрамына шек бойынша (2 кесте мәліметтері негізінде):

,

,

,

,

,

,

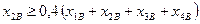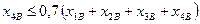Кен құрамы мен мінездеме бойынша (3 кесте мәліметтері негізінде):

,

,

,

,

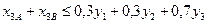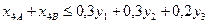Сонымен қатар, айнымалыларды пайдалану диапазоны бойынша:

,

,

,

,

5.7 суретте көрсетілгендей, C3:D6 ұяшықтар диапазонын айнымалыларға бөлейік, ал F3:F5 ұяшықтар диапазонын 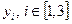айнымалырға бөлейік.

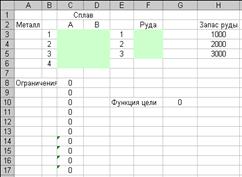
5.7-сурет – Қорытпа құрамын анықтау есебінің бастапқы мәліметтер.

G9 ұяшығына мақсатты функциян енгізейік

=200*СУММ(СЗ:С6)+210*СУММ(D3:D6)-30*F3-40*F4-50*F5

С8:С17 ұяшықтар диапазонына сол жақ шектерді енгізейік және оларды барлық айнымалылар сол жақта болатындай, ал тең емес белгілері – кем немесе тең болатындай түрге келтірейік:

=СЗ-0,8*СУММ(СЗ:С6),

=С4-0,3*СУММ(СЗ:С6),

=D4-0,6*СУММ(D3:D6),

=0,4*СУММ(D3:D6)-D4,

=0,3*СУММ(D3:D6)-D5,

=D6-0,7*СУММ(D3:D6),

=СУММ(СЗ:D3)-0,2*$F$3-0,1*$F$4-0,05*$F$5,

=СУММ(С4:D4)-0,1*$F$3-0,2*$F$4-0,05*$F$5,

=СУММ(С5:D5)-0,3*$F$3-0,3*$F$4-0,7*$F$5,

=СУММ(С6:D6)-0,3*$F$3-0,3*$F$4-0,2*$F$5.

НЗ:Н5 ұяшықтар диапазонына қорды бар кен санын енгізейік. 5.8 суретте көрсетілгендей Сервис, Шешім іздеу командаларын таңдап, Шешім іздеу терезесін толтырайық.

Қажетті ұяшықтарды және шектерді толтырғаннан кейін Орындау батырмасын басыңыз.

5.8-сурет – қорытпа құрамын анықтау есебіндегі Шешім іздеу терезесі

3-тапсырма. Кəсіпорын төрт түрлі өнім шығарады: Ө1, Ө2, Ө3, Ө4. Оны өндіруде үш ресурс қолданылады: еңбек, шикізат жəне құрал-жабдық. Əр ресур бойынша шығын төмендегі 5.4 кестеде берілген:

5.4-кесте – Өнімді шығаруға жұмсалатын ресурстар нормасы

Ресурс	Өнім түрі	Ресурс көлемі
Ө1	Ө2	Ө3	Ө4
Еңбек
Шикізат
Құрал-жабдықтар

Өнімді сатқаннан түсетін пайда: Ө1 – 60, Ө2 – 70, Ө3 – 120, Ө4 – 130.

Кəсіпорынның пайдасын максималдау үшін əр өнім бойынша өндірудің тиімді жоспарын құрыңыз.

6 Транспорттық есеп (не трогать)

6.1 Транспорттық есептің математикалық моделі

Жалпы түрде транспорттық есепті былай түсіндіруге болады: m пунктте: A1, …, Am біртекті жүк бар. Жүктің көлемі сəйкесінше a1, …, am. Бұл жүкті тұтынушыларға (B1, …, Bn) жеткізу керек. Олардың сұранысы – b1, …, bn. Тасымалдау құны i-ші (i=1,m) пункттен j-ші (j=1,n) пунктке дейін cij. Тұтынушылардың сұраныстарын толық қанағаттандыратын жəне транспорттық шығындар минималды болатын жоспар құрыңыз.

Есепті математикалық жазу түрінде былай беруге болады:

(1)

(2)

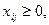
(3)

Сонымен, берілгені: сызықтық функция (1), шарттар (3), шектеулер жүйесі (2). Шешімдер жиынынан (2) сызықтық функцияның (1) минимумы болатын теріс емес шешімін тау керек.

Егер жүк жеткізушідегі жүктің жиынтық көлемі тұтынушыға керек жүктің жиынтық көлеміне тең болса, онда транспорттық есеп жабық (балансталған) деп аталады: яғни, төмендегі теңдік орындалса:

Егер төмендегі шарттардың бірі орындалса, онда транспорттық есеп ашық (балансталмаған) деп аталады:

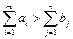
Транспорттық есептің шешімі болу үшін ашық модельді жабық модельге айналдыру керек.

- Егер шарты орындалса, онда фиктивті (n+1)-ші пунктті

Bn+1 кіргіземіз, яғни есепке қосымша баған кіргізіледі. Бұл тұтынушының сұранысы мынаған тең болады:

Тасымалданатын жүктің құны нөлге тең болады, яғни, .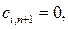

Егер шарты орындалса, онда фиктивті (m+1)-ші жеткізушіні Am+1 кіргіземіз, яғни, есепке қосымша жол кіргізіледі. Бұл жеткізушідегі жүк мынаған тең деп алынады:

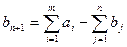
Тасымалданатын жүктің құны нөлге тең болады, яғни, .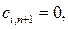

Ашық модельді жабық модельге айналдырғанда мақсаттық функция өзгермейді, өйткені қосымша жүк тасымалына сəйкес келетін қосылғыштар нөлге тең.

6.2 Тақырып бойынша тапсырмалар

1-тапсырма. Транспорттық есеп

Шешім іздеу құралы қолданылатын тағы бір мысалды қарастырайық. Төрт фабрика және оның өнімдерін өткізу бес орталықтарға ие фирма бар деп шамалайық. Күніне 200, 150, 225 және 175 өндіріс мүмкіншіліктерге ие фирма фабрикалары Денвер, Бостон, Новый Орлеан және Даллас қалаларында орналасқан. Күніне 100, 200, 50, 250 және 150 қажеттіліктерге ие фирма өнімдерін өткізу орталықтары сәйкесінше Лос-Анджелес, Даллас, Сент-Луис, Вашингтон және Атланта сында орналасқан. Өткізу орталығына жіберілмеген фабрикада өнім бірліктерді сақтау күніне 0,75 доллар қымбатқа түседі, ал тұтынушының өткізу орталығында тапсырыс берілген, бірақ мерзімі өткен өнім бірлігі үшін күніне 2,5 доллар қымбатқа түседі. Фабрикадан өткізу орталықтарға шейін өнім бірлігін тасымалдау құны 6.1 кестеде көрсетілген.

6.1-кесте– Транспорттық шығындар

Қалалар	Лос-Анджелес	Даллас	Сент-Луис	Вашингтон	Атланта
Денвер	1,5		1,75	2,25	2,25
Бостон	2,5		1,75		1,5
Новый Орлеан		1,5	1,5	1,75	1,75
Даллас		0,5	1,75	1,75	1,75

Көліктік шығындарды минималдандыру үшін тасымалдауларды дұрыс жоспарлау қажет.

Бұл модель балансталғандықтан (өдірілген өнім көлемінің сомасы оның ішіндегі қажеттіліктер көлемінің сомасына тең бөлінген), өнім жеткізбеушілік және қоймалауға байланысты шығындарды санамауға болады. Басқа жағдайда келесі мәліметтерді енгізу керек:

- артық өндіру жағдайында – жалған өткізу орталығын, қоймалау құны кіретін өнім бірлігінің бірдей тасымалдау құнын, ал тасымалдау көлеміне – өнім артықтарының қоймалау көлемдерін;

- тапшылық жағдайында – жалған фабриканы, өнімді жеткізбеу айып пұлдары кіретін өнім бірлігінің бірдей тасымалдау құнын, ал тасымалдау көлеміне – өткізу орталықтарына жеткізілмеген өнім көлемін.

Бұл есепті шығару үшін оның математикалық моделін құрастырайық. Осындағы белгісіздер тасымалдау көлемі болып табылады. 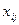– i-нші фабрикадан j-нші өткізу орталыққа тасымалдау көлемі. Мақсатты функция – көліктік шығындардың сомасы, яғни:

,

мұндағы 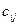– i-нші фабрикадан j-нші өткізу орталыққа өнім бірлігінің тасымалдау құны.

Белгісіздер келесі шектеулерді қанағаттандыру керек:

- тасымалдау көлемі теріс бола алмайды.

- модель балансталғандықтан, бүкіл өнім фабрикадан шығарылу керек, ал бүкіл өткізу орталықтардың қажеттіліктері толығымен қанағаттандырылу керек.

Нәтижесінде келесі модель пайда болады: минималдандыру келесі шектеулерде:

,

,

.

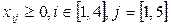мұндағы 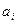– i-нші фабриканың өндіріс көлемі; – j-нші өткізу орталығының сұранысы.

6.1 суретте көрсетілгендей бұл есепті шешу үшін шешім іздеу құралы көмегімен бастапқы мәліметтерді енгізейік.

А1:Е4 ұяшықтарына тасымалдау құнын енгіземіз. А6:Е9 ұяшықтары белгісіздер (тасымалдау көлемі) үшін бөлінген. G6:G9 ұяшықтарына фабрикадағы өндіріс көлемі енгізілген, ал А11:Е11 ұяшықтарына өткізу орталықтарының қажеттіліктері енгізілген.

F10 ұяшығына мақсатты функция енгізілген.

=СУММПРОИЗВ(А1:Е4;А6;Е9)

6.1-сурет– Транспорттық есептің бастапқы мәліметтері

А10:Е10 ұяшықтарына өткізу орталықтарына әкелінетін өнім көлемін анықтайтын келесі формулалар енгізілген

=СУММ(А6:А9),

=СУММ(В6:В9),

=СУММ(С6:С9),

=СУММ(D6:D9),

=СУММ(Е6:Е9),

F6:F9 ұяшықтарына фабрикадан шығарылатын өнім көлемін анықтайтын формулалар енгізілген.

=СУММ(А6:Е6),

=СУММ(А7:Е7),

=СУММ(А8:Е8),

=СУММ(А9:Е9),

6.2 суретте көрсетілгендей Сервис, Шешім іздеу командасын таңдап, ашылған Шешім іздеу терезесін толтырамыз.

6.2-сурет– Транспорттық есеп үшін Шешім іздеусұхбат терезесі

Іздеу параметрлері терезесінде Сызықтық модель тұсында жалау қоюды ұмытпаңыз. 6.3 суретте көрсетілгендей Орындау батырмасын басқаннан кейін шешім іздеу құралы өнім жеткізудің ең тиімді жолын және оған тиісті көліктік шығындарды анықтайды.

6.3-сурет – Транспорттық есептің тиімді шешімі

2-тапсырма. Тағайындаулар туралы есептер

Тағайындаулар туралы есептерді шешудің мысалын қарастырайық. Төрт жұмысшы жұмыстың төрт түрін орындай алады. j-й жұмысының i-м жұмысшымен орындауының бағасы 6.4 суретте A1:D4 диапазонының ұяшықтарында келтірілген.

6.4-сурет - Тағайындаулар туралы есебіндегі жұмыстардың бағалары

Бұл кестеде жолдар жұмысшыларға сәйкес келеді, ал баған – жұмыстарға. Барлық жұмыстар орындалғандай етіп, әрбір жұмысшы тек бір жұмыста ғана болатындай етіп, ал барлық жұмыстардың орындалуының жиынтық бағасы минималды болатындай етіп жұмыс орындау жоспарын құру керек. Берілген есеп теңгерілген, яғни жұмыс саны жұмысшылар санына тең екенін атап көрсету керек. Егерде есеп теңгерілмеген болса, онда оны шешудің алдында есепті теңгеру керек, ол үшін жұмыстың жоғары құндары бар жетпейтін жолдардың немесе бағандардың санын енгізу керек.

Берілген есепті шешу үшін оның математикалық моделін құрайық. Егер i жұмысшымен j жұмысы орындалса, онда 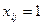, егерде i жұмысшымен j жұмысы орындалмаса, онда . Онда модель келесі түрге ие: минимизациялау келесі шектеулерде:

,

,

.

Шешімді іздеу құралдарының көмегімен бұл есепті шығару үшін белгісіздерге F2:I5 ұяшықтарының диапазонын бөлейік. J1ұяшығына жұмыстардың бағасын есептейтін мақсаттық функцияны енгіземіз:

=СУММПРОИЗВ(F2:I5;A1:D4),

6.5 суретте көрсетілгендей шектеулердің сол жақтарына сәйкес келетін формулаларды енгіземіз.

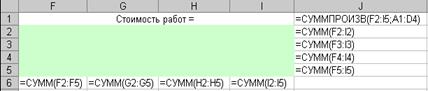
6.5-сурет - Тағайындаулар туралы есептегі шектеулердің сол жақтары

Бұдан кейін Сервис, Поиск решения командасын таңдаймыз және ашылған Поиск решения сұхбат терезесін 6.6 суретте көрсетілгендей толтырамыз.

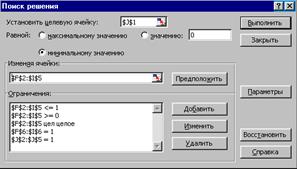
6.6-сурет – Тағайындаулар туралы есебінің Поиск решения сұхбат терезсі

Параметры поиска решения сұхбат терезесінде Линейная модель флажогын орнатуды ұмытпаңыз. Выполнить батырмасын басқаннан кейін шешімді іздеу құралы 6.7 суретте келтірілген тиімді ешімді табады.

6.7-сурет– Тағайындаулар туралы есебіндегі жұмыстардың тиімді жоспары

Дата добавления: 2014-11-07