
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Булевая алгебра
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Тема 1. Булевая алгебра. Системы счисления.
Содержание отчета:
1. Тема работы.
2. Условие и решение задания.
1.1. Основные понятия и определения
Алгебра логики – раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Высказывание – повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Основы алгебры логики заложил в середине XIX века английский логик Джордж Буль в работе «Математический анализ логики». Он перенес на логику законы и правила алгебраических действий, ввел логические операции, предложил способ записи высказываний в виде логических формул. Например, высказывание «Если идет дождь и прогулка отменяется, то я останусь дома» можно записать в виде формулы: 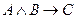 .
.
Высказывания могут быть простыми или сложными. Простым называется высказывание, которое не содержит в себе других высказываний. Простые высказывания в алгебре логики обозначают прописными буквами латинского алфавита. Например: А ={Число 25 кратно 5}. Сложные высказывания на естественном языке образуются объединением простых высказываний с помощью логических связок, которые в алгебре логики заменяются на логические операции.
В алгебре логики не интересуются содержанием высказывания, а определяют его истинность или ложность. Значение истинности простого высказывания определяется по договоренности, а сложного высказывания – по таблице истинности.
Логическое выражение (логическая формула) – это выражение, содержащее логические переменные и знаки логических операций. Результатом вычисления логического выражения является истина или ложь (1 или 0).
Логическая функция – это функция, определенная на множестве истинностных значений (истина, ложь) и принимающая значение из того же множества. Например: 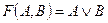 - логическая функция двух переменных – А и В.
- логическая функция двух переменных – А и В.
Если высказывание истинно при всех значениях входящих в него переменных, то такое высказывание называется тождественно истинным или тавтологией (обозначается константой 1). Например, высказывание «Дождь будет или дождя не будет» всегда истинно. Математическая запись данного высказывания: 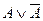 .
.
Если высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется тождественно ложным (обозначается константой 0). Например, высказывание «Компьютер работает, и компьютер не работает» является тождественно ложным. Математическая запись этого высказывания: 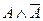 .
.
1.2. Логические операции
Логическое отрицание (инверсия) образуется из высказывания с помощью логических связок «не» или «неверно, что …».
Обозначение инверсии: НЕ А, NOT A, Ø А, 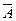 .
.
Пример. Высказывание «7£5» является отрицанием высказывания «7>5».
Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью логической связки «и».
Обозначение конъюнкции: А И В, А AND B, A × B, A & B, А Ù В.
Пример. A Ù B = {Число 128 четное и трехзначное}.
Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью логической связки «или».
Обозначение нестрогой дизъюнкции: А ИЛИ В, A OR B, A + B, А Ú В.
Пример. A Ú B = {Студент едет в автобусе или читает книгу}.
Обозначение строгой дизъюнкции: A XOR B, 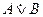 .
.
Пример. 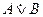 = {Завтра дождь будет или не будет}.
= {Завтра дождь будет или не будет}.
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью логической связки «если …, то …».
Обозначение импликации: 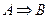 ,
, 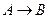 .
.
А называют посылкой, В – заключением.
Пример. А ® В = {Если на улице дождь, то асфальт мокрый}.
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью логической связки «… тогда и только тогда, когда …».
Обозначение эквивалентности: А ~ B, 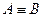 ,
, 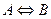 ,
, 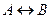 .
.
Пример. 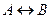 = {Две прямые параллельны тогда и только тогда, когда они не пересекаются}.
= {Две прямые параллельны тогда и только тогда, когда они не пересекаются}.
Таблица истинности:
| A | B | 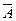
| 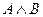
| 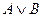
| 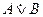
| 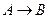
| 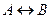
|
Количество строк в таблице истинности равно 2n, где n – число логических переменных, входящих в логическое выражение.
При вычислении значения логического выражения (формулы) логические операции выполняются в определенном порядке, согласно их приоритету:
1) инверсия 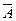 ;
;
2) конъюнкция 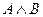 ;
;
3) дизъюнкция 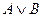 ;
;
4) импликация 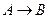 ;
;
5) эквивалентность 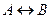 .
.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример. Дана формула 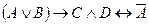 .
.
Порядок вычисления:
1) 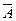 - инверсия;
- инверсия;
2) 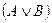 - дизъюнкция в скобках;
- дизъюнкция в скобках;
3) 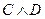 - конъюнкция;
- конъюнкция;
4) 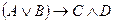 - импликация;
- импликация;
5) 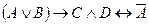 - эквивалентность.
- эквивалентность.
1.3. Логические законы и правила преобразования логических выражений
1.3.1. Законы однопарных элементов:
а) универсального множества:
А Ú 1 = 1; А Ù 1 = А;
б) нулевого множества:
А Ú 0 = А; А Ù 0 = 0.
1.3.2. Законы отрицания:
а) двойного отрицания:
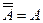 ;
;
б) дополнительности:
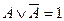 ;
; 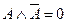 ;
;
в) двойственности (де Моргана):
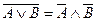 ;
; 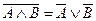 .
.
1.3.3. Комбинационные законы:
а) тавтологии:
А Ú А = А; А Ù А = А;
б) коммутативные:
А Ú В = В Ú А; А Ù В = В Ù А;
в) ассоциативные (сочетательные):
А Ú (В Ú С) = (А Ú В) Ú С; А Ù (В Ù С) = (А Ù В) Ù С;
г) дистрибутивные (распределительные):
А Ù (В Ú С) = (А Ù В) Ú (А Ù С);
А Ú (В Ù С) = (А Ú В) Ù (А Ú С);
д) закон абсорбции (поглощения):
А Ú (А Ù В) = А; А Ù (А Ú В) = А;
е) склеивания:
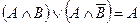 ;
; 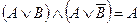 .
.
1.3.4. Правила замены операции импликации:
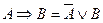 ;
; 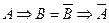 .
.
1.3.5. Правила замены операции эквивалентности:
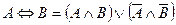 ;
;
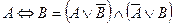 ;
;
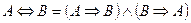 .
.
Пример. Упростить выражение: 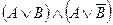 . Согласно закону дистрибутивности:
. Согласно закону дистрибутивности: 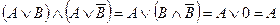 .
.
1.4. Логические элементы
Логический элемент – преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдает значение логического отрицания, логического сложения или логического умножения этих высказываний.
Цифровой сигнал – это сигнал, который может принимать только одно из двух установленных значений.
Логический элемент «НЕ» (инвертор) реализует операцию отрицания. Если на вход поступит сигнал 1, то на его выходе будет 0 и наоборот.
Условное обозначение инвертора:
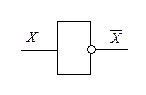
Логический элемент «И» (конъюнктор) реализует конъюнкцию двух или более логических значений.
Условное обозначение конъюнктора:
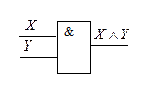
Логический элемент «ИЛИ» (дизъюнктор) реализует дизъюнкцию двух или более логических значений.
Условное обозначение дизъюнктора:
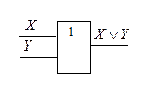
Логический элемент «И – НЕ» реализует отрицание конъюнкции.
Условное обозначение «И – НЕ»:
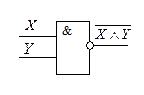
Логический элемент «ИЛИ – НЕ» реализует отрицание дизъюнкции.
Условное обозначение «ИЛИ – НЕ»:
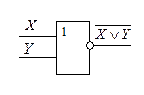
|
|
Дата добавления: 2014-11-07; Просмотров: 605; Нарушение авторских прав?; Мы поможем в написании вашей работы!