Момент инерции

При изучении вращения твердых тел будем пользоваться понятием момента инерции. Моментом терции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстояний до рассматриваемой оси:

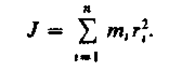
В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. Величина rв этом случае есть функция положения точки с координатами х, у, z.

Рис. 23

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 23). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины drсвнутренним радиусом rи внешним r+dr.Момент инерции каждого полого цилиндра dJ = r²dm(так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно г), где dm — масса всего элементарного цилиндра; его объем 2prhdr. Если r— плотность материала, то dm = 2prhrdr и dJ = 2phrr³dr. Тогда момент инерции сплошного цилиндра

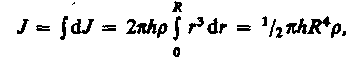
но так как pR²h— объем цилиндра, то его масса m = pR²hr, а момент инерции

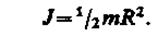
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

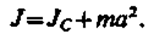(16.1)

В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).

Таблица 1

Тело	Положение оси	Момент инерции
Полый тонкостенный цилиндр радиусом R Сплошной цилиндр или диск радиусом R Прямой тонкий стержень длиной l Прямой тонкий стержень длиной l Шар радиусом R	Ось симметрии   Тоже   Ось перпендикулярна стержню и проходит через его середину Ось перпендикулярна стержню и проходит через его конец Ось проходит через центр шара	тR^2   1/2 тR^2   1/12 ml^2 1/3 ml^2   2/5 тR^2

Дата добавления: 2014-11-07