Вращательного движения твердого тела

Момент силы. Уравнение динамики

Моментом силы F относительно неподвижной точки Оназывается физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):

М = [rF].

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F.

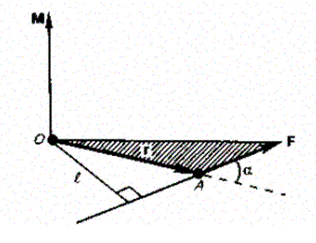
Рис. 25.

Модуль момента силы

где a — угол между г и F; r×sina = l — кратчайшее расстояние между линией действия силы и точкой О— плечо силы.

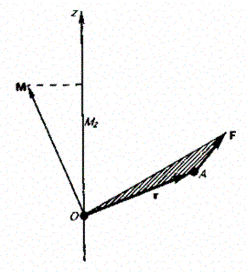
Рис. 26

Моментом силы относительно неподвижной оси z называется скалярная величина М_z, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М_г не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

M_z = [rF]_z.

Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложена в точке В, находящейся от оси z на расстоянии г, a — угол между направлением силы и радиусом-вектором г. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dj точка приложения В проходит путь ds=rdj и работа равна произведению проекции силы на направление смещения на величину смещения:

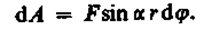
Рис. 27

Учитывая (18.1), можем записать

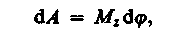
где 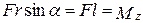— момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA = dT, но 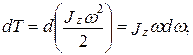поэтому 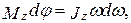или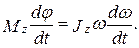

Учитывая, что , получаем

(18.3)

Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Можно показать, что если ось z совпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство

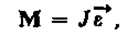(18.4)

где J — главный момент инерции тела (момент инерции относительно главной оси).

Дата добавления: 2014-11-07