Математическая модель поставленной задачи

Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии и график полученной экспериментальной зависимости.

Вычислить коэффициенты функциональной зависимости, соответствующей варианту задания. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку. Вычислить индекс корреляции.

Рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.

Ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.

Рекомендации к выполнению курсовой работы

Постановка задачи

Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы.

x i	x 1	x 2	x 3	x 4	x 5	x 6	x 7	…	xn
y i	y 1	y 2	y 3	y4	y5	y 6	y 7	…	yn

Необходимо провести регрессионный анализ экспериментальных данных и построить аналитическую зависимость вида

Y = f (x, a ₀ a ₁,..., a_k)

ВАРИАНТЫ ЗАДАНИЙ

Вариант №1. P(s)=As³+Bs²+Сs+D

S	0,00	1,00	1,50	2,00	2,50	3,00	3,50	4,00	4,50	5,00
P	10,00	50,10	39,58	15,40	23,68	33,60	57,78	100,90	149,50	256,00

Вариант № 2. G(s)=Ae^bs

s	0,5	1,5		2,5		3,5		4,5
G	3,99	5,65	6,41	7,71	11,215	17,611	27,83	38,19	39,3

Вариант № 3. K(s)=As^b

s	0,5		1,5		2,5		3,5
K	1,65	2,1		2,1	2,3	2,4	2,22	2,59

Вариант № 4. V(s)=As^bе^Cs

s	0,2	0,7	1,2	1,7	2,2	2,7	3,2
V	2,3198	2,9569	2,3999	6,4357	6,5781	6,9459	14,6621

Вариант № 5. W(s)= 1 /(As+B)

s
W	0,529	0,298	0,267	0,171	0,156	0,124	0,1	0,078	0,075

Вариант № 6. Q(s)=As²+Bs+C

s		1,25	1,5	1,75		2,25	2,5	2,75
Q	5,21	4,196	3,759	3,672	4,592	4,621	5,758	7,173	9,269

Вариант № 7. Y=x/(Ax+B)

x		3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9
Y	0,61	0,6	0,592	0,58	0,585	0,583	0,582	0,57	0,572	0,571

Вариант № 8. V=1/(A+Be^-U)

U		2,5		3,5		4,5		5,5
V	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

Вариант № 9. R=At^B-14,5

t
R	2,11	5,2	5,15	19,27	18,2	30,37			30,22	31,2

Вариант № 10. Z=At⁴+Bt³+Ct²+Dt+K

t	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Вариант № 11. Y=Ax³+Cx+D

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 12. R=Ch²+K

h		1,5		2,5		3,5		4,5
R	7,5	14,25	23,7	25,86	50,7	68,25	88,5	111,5

Вариант № 13. Z=At⁴+Ct²+K

t		1,5		2,5		3,5		4,5
Z	2,2	10,6	35,6		191,1	359,2	618,7	997,9	1598,5

Вариант № 14. Z=At⁴+Bt³+Dt+K

t		1,5		2,5		3,5		4,5
Z	2,21	9,83	30,5	74,5	155,2	288,86	494,5	794,69	1214,6

Вариант № 15. Z=At⁴+Bt³+Ct²+K

t		1,5		2,5		3,5		4,5
Z	5,25	13,4	31,29	64,64	121,23	209,94	341,23	527,14

Вариант № 16. Z=At⁴+Dt+K

t	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Z	0,5	1,35	2,37	3,8	5,8	8,65	12,57	18,05	0,86

Вариант № 17. Y=Ax³+D

x		0,2	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Y	3,6	3,59	3,65	3,96	4,12	4,86	5,67	6,85	8,42	10,47

Вариант № 18. V=A+Be^U

U		0,5		1,5		2,5		3,5
V	3,597	4,597	5,5984	7,5987	11,269		26,5096	42,1599

Вариант № 19. G=D/L+K

L		1,13	1,25	1,38	1,5	1,63	1,75	1,88
G	3,8	3,2	2,6	2,2	1,8	1,6	1,4	1,3	1,1

Вариант № 20. Z=At⁵+Bt⁴+Ct³+Dt²+Kt+L

t	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Вариант № 21. R= At⁵+Bt⁴+Ct³+Dt²+L

t
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант № 22. G= At⁵+Bt⁴+Dt²+Kt+L

t		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 23. Y= At⁵+Ct³+Dt²+Kt+L

t		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 24. Y= At⁵+Bt⁴+Ct³+Kt+L

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 25. R= At⁵+Ct³+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 26. R= At⁵+Dt²+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 27. W= At⁵+Dt²+L

t		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 28. V= At⁵+L

t		1,1	1,2	1,3	1,4	1,5	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5

Вариант № 29. R=Ch²+Dh+K

h
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант № 30. G=DL+K

L		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 31. Y=Ax³+Bx²+Cx+D

x		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 32. R=At^B

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 33. W(s)=1/(Bs+C)

s		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 34. V(s)=s^bе^Cs

s		1,1	1,2	1,3	1,4	1,5	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5

Вариант № 35. Y=x/(Ax+B)

x		1,5		2,5		3,5		4,5
Y	0,214	0,221	0,2237	0,2258	0,2262	0,2268	0,2275	0,2283	0,2288

Вариант № 36. V(s)=Asе^Cs

s
V	43,75	32,25	17,83	8,76		1,77	0,76	0,32

Вариант № 37. V(s)=As^bе^s

s		1,5		2,5		3,5		4,5
V	6,5	8,71	12,67	18,6	27,63	42,61	65,6	101,86

Вариант № 38. V(s)=As^B

s		2,3	2,9	4,1	5,2	5,9	6,8	8,1	9,2
V	2,4		58,5	165,5	337,5		754,5

Вариант № 39. K(s)=Ae^Sb

s		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
K	2,2	3,73	6,25	10,49	17,61	29,65	49,84	140,9	237,1

Вариант № 40. K(h) =1/(A+Be^-h)

h		2,5		3,5		4,5		5,5
K	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

С помощью электронной таблицы MS Excel выполнить следующие действия.

Метод наименьших квадратов используется при обработке реальных количественных данных, полученных в результате всевозможных научных опытов, технических испытаний, астрономических, геодезических и т.п. наблюдений.

Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы:

x i	x 1	x 2	x 3	x 4	x 5	x 6	x 7	…	xn
y i	y 1	y 2	y 3	y4	y5	y 6	y 7	…	yn

Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.

Идея метода наименьших квадратов заключается в том, что функцию

Y = f (x, a ₀ a ₁,..., a_k)

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений y _i от расчетных Y_i была наименьшей (рис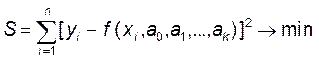. 1):

(1)

Задача сводится к определению коэффициентов a_i из условия (1). Для ее решения необходимо составить систему уравнений

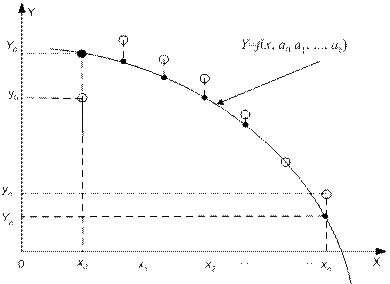
Рис. 1. Геометрическая интерпретация метода наименьших квадратов

Если параметры a_i входят в зависимость Y = f (x, a ₀ a ₁,..., a_k) линейно, то получим систему из k -линейных уравнений с k неизвестными:

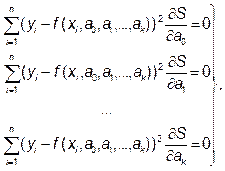(2)

Зная коэффициенты a_i, являющиеся решением системы (2), можно составить искомую функцию Y = f (x, a ₀, a ₁,..., a_k).

3.1 Подбор параметров линейной функции

Пусть необходимо определить параметры функции :Y = a ₀ + a ₁ x.

Составим многочлен (1) для заданной функции:

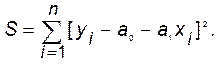
Сформируем систему линейных уравнений (2) решив которую, определим коэффициенты функции Y = a ₀ + a ₁ x:

,

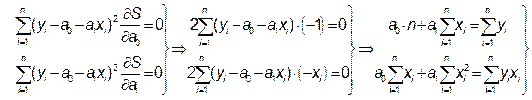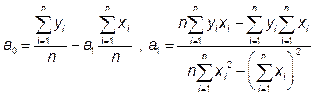. (3)

Дата добавления: 2014-11-07