Надежность систем с облегченным резервом

Как отмечалось в предыдущих лекциях, ненагруженный резерв более эффективен, чем нагруженный, и количественно показатели эффективности зависят от законов распределения наработки до отказа отдельных элементов резервированной системы.

Основным моментом, который может сказаться на оценке надежности является то, что предположение = const является довольно условным, поскольку, особенно при отсутствии технического обслуживания, очередной работающий элемент эксплуатируется до полного износа (физически должна возрастать). Поэтому принятое экспоненциальное распределение наработки элементов, переходящих из резервных в рабочие, использовалось только с целью упрощения расчетов.

Ненагруженный резерв в рамках принятых допущений не всегда осуществим. Например, в авиа- и судовых системах как основные, так и резервные элементы подвержены вибрации, ударам, повторно-статическим нагрузкам, перепадам температур и т. п. Поэтому не включенные в работу резервные элементы будут иметь некоторую 0, то есть они также изнашиваются, но менее интенсивно.

Поэтому, в ряде практических случаев, уместно применять облегченный резерв:

(подключение резервных элементов (РЭ) к цепям питания для прогрева и удержания требуемых значений параметров;

(внешние нагрузки и воздействия, приводящие к изменению свойств материалов, рабочих параметров и т. п.

При этом, РЭ будут иметь некоторую интенсивность отказов _р 0.

Рассмотрим систему, состоящую из равнонадежных основного (ОЭ) и резервного (РЭ) элементов. Элементы невосстанавливаемые.

События, обеспечивающие безотказную работу (БР) системы за наработку (0, t):

A = {БР системы за наработку (0, t)};

A₁ = {БР ОЭ за наработку (0, t)};

A₂ = {отказ ОЭ в момент < t, включение РЭ и БР его на интервале (t - )}.

Событие A представляет сумму событий A₁ и A₂

A = A₁ 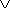A₂

ВБР системы за наработку (0, t), т.е. к наработке t равна сумме вероятностей событий A₁ и A₂:

P(A) = P(A₁ ) + P(A₂),

где P(A) = P_с(t) – ВБР системы к наработке t;

P(A) = P₀ (t) – ВБР ОЭ к наработке t (за интервал (0, t));

P(A) = P_р (t) – ВБР РЭ к наработке t, при условии, что ОЭ отказал.

При известном законе распределения наработки ОЭ вычисление P₀ (t) не составляет труда, подробнее рассмотрено определение Pр (t).

Для этого событие A₂ раскладывается на составляющие:

A₂₁ = {отказ ОЭ при наработке < t };

A₂₂ = {БР РЭ до наработки – момент включения его в работу};

A₂₃ = {БР РЭ от до t, т.е. за интервал (t - )}.

Очевидно, событие A₂ выполнится при одновременном выполнении всех событий:

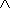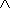A₂ = A₂₁ A₂₂ A₂₃;

События A₂₁, A₂₂, A₂₃ являются зависимыми, но поскольку они представляют ВБР или ВО элементов, наработки до отказа которых описываются своими законами распределения, то вероятность события A₂ равна произведению вероятностей событий:

P(A₂ ) = P(A₂₁ ) · P(A₂₂ ) · P(A₂₃).

Соответствующие вероятности определяются:

Выделяется бесконечно малый интервал [, + d ] и определяется вероятность отказа ОЭ в интервале [, + d ]:

f₀ () = - dP₀ () / d – ПРО ОЭ.

ВБР РЭ до момента отказа ОЭ

Pр () = P(A₂₂ )

ВБР РЭ от момента включения в работу до t

Pр (t - ) = P(A₂₃).

Тогда ВБР ОЭ в течение наработки [, + d ] при условии, что ОЭ отказал, равна:

Pр () · Pр (t - ) · f₀ () d.

Полученное выражение не равно P(A₂ ), поскольку выражает ВБР за выделенный бесконечно малый интервал наработки вблизи .

Поскольку < t, то из полученного выражения искомая вероятность P_р (t) = P(A₂ ), получена интегрированием выражения по всем от 0 до t.

Окончательно:

Тогда ВБР резервируемой системы с облегченным резервом:

Аналогично, ВБР системы, состоящей из n равнонадежных элементов:

где индекс (n-1)с означает, что ВБР и ПРО относятся к системе, при отказе которой включается рассматриваемый n –й элемент.

При экспоненциальном распределении наработки до отказа элементов составляющие расчетного выражения принимают вид:

P_р () = exp(- _p );

P_р (t - ) = exp { - _раб (t - )};

f₀ () = _раб exp (- _раб · );

P₀ (t) = exp (- _раб · t),

где _раб – ИО элементов в рабочем режиме; _p – ИО элементов в режиме резерва.

При наличии одного ОЭ и одного РЭ (n = 2), ВБР определяется:

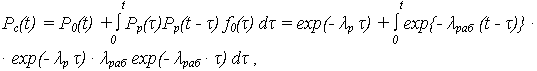
окончательно:

P_с (t) = exp (- _раб · t) [ 1 + _раб {1 - exp (- _pt)} / _p ].

Для системы из n элементов с экспоненциальной наработкой до отказа

где

Расчеты для систем с облегченным резервом имеют объективные трудности, поскольку очень трудно учесть как влияет нагрузка, внешние воздействия на характеристики надежности.

Средняя наработка до отказа системы из n элементов:

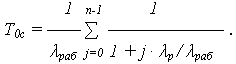
Для практических расчетов систем с облегченным резервированием в случае, если ОЭ имеет распределением наработки P₀ (t) = exp (- _раб · t) и идентичные резервные элементы (РЭ)

Pр (t) = exp (- _pt) – для(n - 1) резервных элементов,

ВБР системы может быть приближенно определена по выражению:

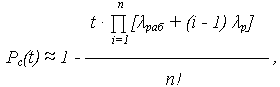
где n – общее число элементов системы.

Например, при n = 2 (k = 1, m = 1)

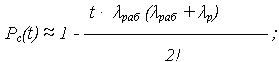
при n = 3 (k = 2, m = 1)

Дата добавления: 2014-10-15