
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы с резервированием. Общие понятия
|
|
|
|
Работоспособность систем без резервирования требует работоспособности всех элементов системы. В сложных технических устройствах без резервирования никогда не удается достичь высокой надежности даже, если использовать элементы с высокими показателями безотказности.
Система с резервированием – это система с избыточностью элементов, т. е. с резервными составляющими, избыточными по отношению к минимально необходимой (основной) структуре и выполняющими те же функции, что и основные элементы.
В системах с резервированием работоспособность обеспечивается до тех пор, пока для замены отказавших основных элементов имеются в наличии резервные.
Структурное резервирование может быть:
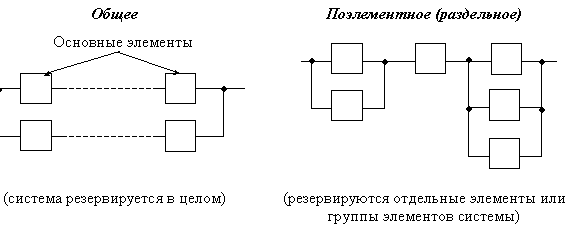
По виду резервирование подразделяют на:
· пассивное (нагруженное) – резервные элементы функционируют наравне с основными (постоянно включены в работу);
· активное (ненагруженное) – резервные элементы вводятся в работу только после отказа основных элементов (резервирование замещением).
При нагруженном резервировании резервные элементы расходуют свой ресурс, имеют одинаковое распределение наработок до отказа и интенсивность отказов основных  о и резервных
о и резервных  н элементов одинакова (
н элементов одинакова ( о =
о =  н).
н).
При нагруженном резервировании различие между основными и резервными элементами часто условное. Для обеспечения нормальной работы (сохранения работоспособности) необходимо, чтобы число работоспособных элементов не становилось меньше минимально необходимого.
Разновидностью нагруженного резервирования является резервирование с облегченным резервом, т. е. резервные элементы также находятся под нагрузкой, но меньшей, чем основные. Интенсивность отказов резервных элементов  об ниже, чем у основных
об ниже, чем у основных  о, т. е.
о, т. е.  о >
о >  об.
об.
При нагруженном резервировании резервные элементы не подвергаются нагрузке, их показатели надежности не изменяются и они не могут отказать за время нахождения в резерве, т. е. интенсивность отказов резервных элементов  х = 0.
х = 0.
Примеры ненагруженного резервирования:
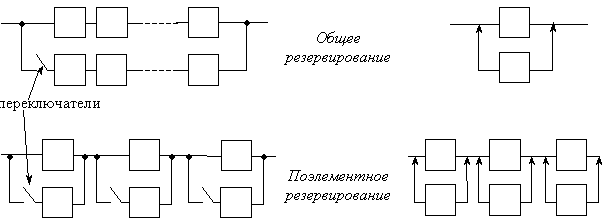
Резервные элементы включаются в работу только после отказа основных элементов. Переключение производится вручную или автоматически (автоматически – включение резервных машин и элементов в энергетике, в бортовых сетях судов и самолетов и т. д.; вручную – замена инструмента или оснастки при производстве, включение эскалаторов в метро в часы «пик» и т. д.).
Разновидностью ненагруженного резервирования является скользящее резервирование, когда один и тот же резервный элемент может быть использован для замены любого из элементов основной системы.
Если рассмотреть два характерных вида резервирования:
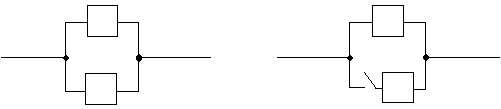
то очевидно, что при равенстве числа основных и резервных элементов ненагруженный резерв обеспечивает большую надежность. Но это справедливо только тогда, когда перевод резервного элемента в работу происходит абсолютно надежно (т. е. ВБР переключателя должна быть равна 1,0). Выполнение этого условия связано со значительными техническими трудностями или является иногда нецелесообразным по экономическим или техническим причинам.
Обозначим:
n – число однотипных элементов в системе;
r – число элементов, необходимых для функционирования системы.
Кратность резервирования – это соотношение между общим числом однотипных элементов и элементов, необходимых для работы системы:
k = (n - r)/r.
Кратность резервирования может быть целой, если r = 1, или дробной, если r > 1.
Например:
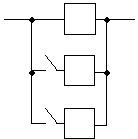
| r = 1, k = (3 - 1)/1 = 2. |
Контрольные вопросы:
1. Основные цели и задачи расчета показателей надежности систем?
2. Определите состав рассчитываемых показателей безотказности системы?
3. Перечислите и поясните основные этапы расчета надежности систем?
4. Что такое структура надежности?
5. Что такое математическая модель расчета надежности?
6. Какие виды резервирования существуют. В чем отличие нагруженного и ненагруженного резервирования?
7. Что такое кратность резервирования и в чем отличие целой и дробной кратности?
Глава 9. НАДЕЖНОСТЬ ОСНОВНОЙ СИСТЕМЫ
Основные системы (ОС) являются простейшими техническими системами, в которых отказ одного элемента приводит к отказу всей системы.
Работоспособность основной системы обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии.
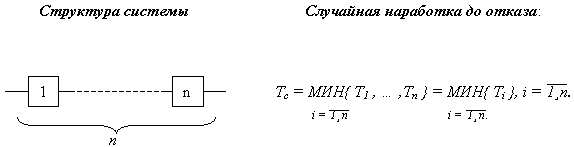
Поскольку события, заключающиеся в работоспособности элементов системы, являются независимыми, то
| вероятность безотказной работы (ВБР) ОС: | 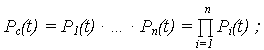
|
| вероятность отказа (ВО) ОС: | 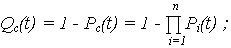
|
При идентичных элементах ОС P1(t) = … = Pn(t) = P(t):
| ВБР: | Pс(t) = P n(t); | ВО: | Qс(t) = 1 - P n(t). |
Поскольку на участке нормальной эксплуатации наработку до отказа можно описать экспоненциальным распределением каждого элемента
Pi(t) = exp(- i · t),
i · t),
где  i = const, то
i = const, то
| ВБР ОС: | 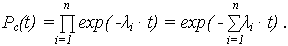
|
Используя уравнение связи показателей безотказности, выражающее ВБР любого объекта, в том числе и системы
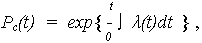
и полагая
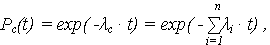
получаем, что интенсивность отказов (ИО) ОС равна сумме ИО элементов:
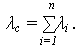
В общем случае, для любого распределения наработки ИО системы равна:

Для n идентичных элементов  1(t) = … =
1(t) = … =  n(t) =
n(t) =  (t):
(t):
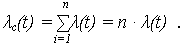
При экспоненциальном распределении наработки до отказа каждого из n элементов ОС Pi(t) = exp(- i · t), где
i · t), где  i = const показатели безотказности ОС определяются:
i = const показатели безотказности ОС определяются:
Неидентичные элементы
 1 = … = 1 = … =  n = n = 
| Идентичные элементы
 1 = … = 1 = … =  n = n = 
| |
| ВБР: | 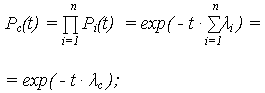
| 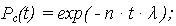
|
| ВО: | 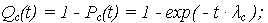
| 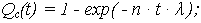
|
| ИО: | 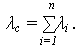
| 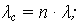
|
| МО наработки до отказа: | 
| 
|
Выражения для МО наработки до отказа получены из формулы:
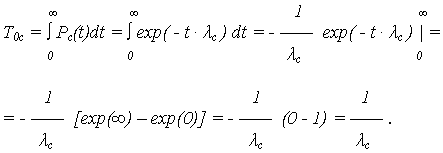
| ПРО: | fс(t) = - d Pс(t)/ dt =  с exp(- t · с exp(- t ·  с); с);
| fс(t) = n ·  · exp(- n · t · · exp(- n · t ·  ) )
|
Таким образом, при экспоненциальной наработке до отказа каждого из n элементов, распределение наработки до отказа ОС также подчиняется экспоненциальному распределению.
Для ОС надежность меньше надежности каждого из элементов. С увеличением числа элементов надежность ОС уменьшается.
Например, при n = 1000, Pi(t) = 0,99, Pс(t) < 10 - 4 и средняя наработка до отказа системы в 1000 раз меньше средней наработки каждого из элементов.
Распределение норм надежности основной системы по элементам.
Рассмотренные модели позволяют определить показатели безотказности ОС по известным показателям надежности элементов – так решается задача при завершении технического проекта, после испытаний опытных образцов системы и составляющих элементов.
Иначе: значения Pi(t) i –х элементов хорошо известны и лишь уточняется значение Pс(t) и сравнивается с заданным в ТЗ на проект. При этом, если Pс(t) получается меньшей, чем в ТЗ, то принимаются меры по ее повышению (резервирование, использование более надежных элементов и т. п.).
На начальной стадии проектирования в ТЗ указывается лишь ВБР проектируемой системы. При проектировании используются как элементы с известной надежностью, так и элементы, о надежности которых можно судить лишь по их аналогам (прототипам). При этом необходима предварительная оценка надежности элементов, которая, в дальнейшем, уточняется в ходе испытания опытных образцов системы и элементов.
Существуют различные способы распределения норм надежности:
· по принципу равнонадежности элементов;
· с учетом данных об аналогах элементов;
· с учетом перспектив совершенствования элементов.
Выбор того или иного способа зависит от имеющейся информации о проектируемой системе.
1. Распределение надежности по принципу равнонадежности элементов:
Задано: по техническому заданию Pс(t); n – число элементов системы.
Распределение наработки до отказа элементов – экспоненциальное.
При идентичных (равнонадежных) элементах ( 1 = … =
1 = … =  i = … =
i = … =  n=
n=  ):
):
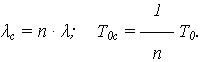
интенсивность отказа i –го элемента: ln Pс(t) = - n ·  · t.
· t.
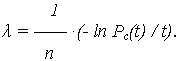
2. Распределение надежности с учетом данных о надежности аналогов.
Задано: по техническому заданию ТЗ Pс(t); n – число элементов системы;
интенсивности отказов аналогов –  аi,
аi, .
.
Определяется доля отказов системы из-за отказов i –го элемента:
ki =  аi /
аi /  ас,
ас,
где 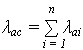 – ИО системы по данным об аналогах.
– ИО системы по данным об аналогах.
Определяется ИО проектируемой системы: Pс(t) = exp(-  с · t)
с · t)
 с = - ln Pс(t) / t (
с = - ln Pс(t) / t ( с > 0; ln P(t) < 0),
с > 0; ln P(t) < 0),
и ИО составляющих элементов:
 i = ki ·
i = ki ·  с.
с.
3. Распределение надежности с учетом перспектив совершенствования элементов.
Задано: по техническому заданию ТЗ Pс(t); n – число элементов системы;
Изменение ИО аналогов за временной период [19XY по 200Z] годы, аппроксимировано выражением  аi =
аi = 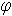 (
(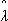 аi, 19 XY),
аi, 19 XY),
где  аi – ИО i –го аналога в 19XY году.
аi – ИО i –го аналога в 19XY году.
По выражению  аi =
аi = 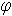 (
(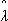 аi, 19 XY) экстраполируется ИО элементов – аналогов к нынешнему году (году проектирования системы), получаются:
аi, 19 XY) экстраполируется ИО элементов – аналогов к нынешнему году (году проектирования системы), получаются:  а1(94),…,
а1(94),…,  аi(94), ….
аi(94), ….
Определяется доля отказов системы из-за отказов i –го элемента:

и ИО элементов системы:
 i = ki ·
i = ki ·  с = ki ·(- ln Pс(t) / t).
с = ki ·(- ln Pс(t) / t).
Принципы распределения показателей надежности по 2 и 3 способам отличаются лишь экстраполяцией значений на год проектирования.
Контрольные вопросы и задачи:
1. Что такое основная система и в чем состоит условие ее безотказной работы?
2. Как определяются показатели безотказности основной системы: ВБР и ИО?
3. Как определяются показатели безотказности основной системы: ПРО и МО наработки до отказа?
4. Какой закон распределения наработки до отказа будет иметь основная система, если законы распределения наработки до отказа элементов являются экспоненциальными (привести доказательство)?
5. В чем заключается необходимость распределения норм надежности между элементами основной системы?
6. Какие существуют способы распределения норм надежности между элементами основной системы, и чем они отличаются?
7. Структура проектируемой системы представляется основной системой, состоящей из 10 элементов «A», 15 элементов «B», 32 элементов «D» и 8 элементов «F». Интенсивности отказов элементов известны и равны:  A = 2 · 10 -6 час -1,
A = 2 · 10 -6 час -1,  B = 4 · 10 -6 час -1,
B = 4 · 10 -6 час -1,  D = 2.5 · 10 -6 час -1,
D = 2.5 · 10 -6 час -1,  F = 5 · 10 -6 час -1. Определить среднюю наработку до отказа T0с и ВБР системы за наработки t1 = 100 час, t2 = 1000 час и в интервале указанных наработок? Определить плотность распределения отказов системы при наработке t2 = 1000 час?
F = 5 · 10 -6 час -1. Определить среднюю наработку до отказа T0с и ВБР системы за наработки t1 = 100 час, t2 = 1000 час и в интервале указанных наработок? Определить плотность распределения отказов системы при наработке t2 = 1000 час?
Ответ: T0с = 5 · 10 3 час, P(t1 ) = 0.98, P(t2 ) = 0.819, Pс(t1, t2 ) = 0.836, f(t2 ) = 1.64 · 10 - 4 час -1.
Глава 10.НАДЕЖНОСТЬ СИСТЕМ С НАГРУЖЕННЫМ РЕЗЕРВИРОВАНИЕМ
Рассматривается система, состоящая из одного основного и (n - 1) резервных элементов.
При условии, что отказы элементов независимы, отказ системы происходит только при отказе всех n элементов.
Структура системы
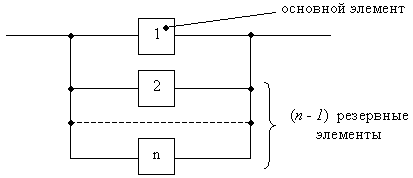
Случайная наработка до отказа:
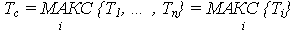
(система работоспособна до тех пор, пока работоспособен хотя бы один элемент).
Поскольку отказ системы есть событие, которое заключается в одновременном появлении событий – отказах всех элементов, то
· вероятность отказа (ВО):
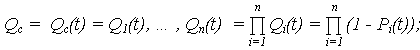
· вероятность безотказной работы (ВБР):
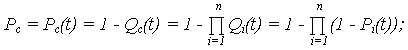
· математическое ожидание (МО) наработки до отказа:
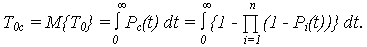
При идентичных элементах системы, т. е. P1(t) = … = Pn(t)
· ВБР:
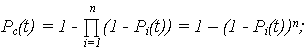
· ВО:
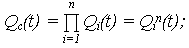
· МО наработки до отказа:
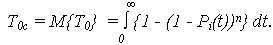
Для системы с экспоненциальной наработкой до отказа каждого из n элементов:
Pi(t) = exp(-  i t),
i t),
где  i = const показатели безотказности:
i = const показатели безотказности:
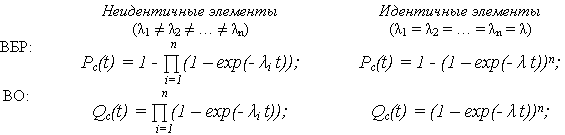
Таким образом, при нагруженном резервировании экспоненциальное распределение наработки до отказа не сохраняется.
При идентичных n элементах системы МО наработки до отказа:
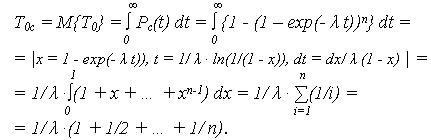
При большом n (n 
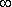 ), T0с
), T0с 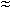 1/
1/  ·(ln n + c), где c = 0.577….
·(ln n + c), где c = 0.577….
При неидентичных элементах:
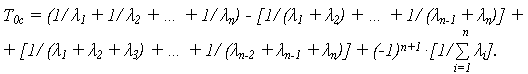
Для системы с n идентичными элементами P1(t) = … = Pn(t) решаются задачи оптимизации (в различных постановках).
1. Определение числа n элементов системы, при котором вероятность отказа (ВО) системы Qс(t) не будет превосходить заданной Qс.
Поскольку Qс(t) = Qin(t), то условие задачи
Qin(t) 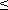 Qс(t).
Qс(t).
Из приведенного неравенства определяется минимально необходимое число элементов:
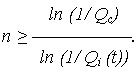
2. Определение надежности n элементов системы из условия, чтобы ВО не превышала заданную Qс.
Из условия Qin(t) 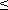 Qс(t), находим ВО I и ВБР Pi(t)
Qс(t), находим ВО I и ВБР Pi(t)  1 - Qi(t).
1 - Qi(t).
Надежность систем с ограничением по нагрузке
Для некоторых систем условия работы таковы, что для работоспособности системы необходимо, чтобы по меньшей мере r элементов из n были работоспособны.
Т. е. число необходимых рабочих элементов – r, резервных – (n - r).
Отказ системы наступает при условии отказа (n – r + 1) элементов.
Если при изменении числа находящихся в работе элементов не наблюдается перегрузки, влияющей на возможность возникновения отказа, то отказы можно считать независимыми.
ВБР такой системы определяется с помощью биномиального распределения.
Для системы, сохраняющей работоспособность при функционировании r из n элементов, ВБР определяется как сумма r, (r + 1), …, (n – r) элементов:
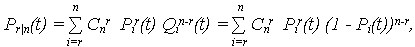
где 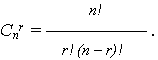
Для идентичных элементов с экспоненциальной наработкой Pi(t) = exp(-  i t),
i t),  i = const (
i = const ( 1 = … =
1 = … =  i = … =
i = … =  n) ВБР:
n) ВБР:
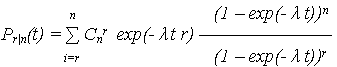
Зависимость надежности системы от кратности резервирования
При целой кратности k (r = 1, n = k + 1) для системы с идентичными элементами и экспоненциальной наработкой до отказа:
· ВБР системы:
Pс(t) = 1 – (1 - exp(-  t))k+1;
t))k+1;
· ПРО системы:
fс(t) = - dPс(t)/ dt = (k + 1)  (1 - exp(-
(1 - exp(-  t))k exp(-
t))k exp(-  t);
t);
· ИО системы:
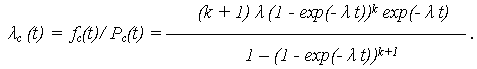
Полагая элементы системы высоконадежными, т. е.  t << 1 (P(t)
t << 1 (P(t) 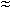 1 -
1 -  t), получены упрощенные выражения:
t), получены упрощенные выражения:
· ВБР системы:
Pс(t) 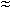 1 – (
1 – ( t))k+1;
t))k+1;
· ПРО системы:
fс(t) 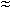 (k + 1)
(k + 1)  k+1 tk;
k+1 tk;
· ИО системы:
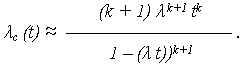
но поскольку  t << 1, то (
t << 1, то ( t)k+1
t)k+1 0, поэтому ИО системы:
0, поэтому ИО системы:
 с (t)
с (t) 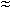 (k + 1)
(k + 1)  k+1 tk = n ·
k+1 tk = n ·  n · tn-1,
n · tn-1,
где n = k + 1.
Полученное выражение  с (t) свидетельствует о том, что при
с (t) свидетельствует о том, что при  = const элементов, ИО системы зависит от наработки, т. е. распределение наработки до отказа системы не подчиняется экспоненциальному распределению.
= const элементов, ИО системы зависит от наработки, т. е. распределение наработки до отказа системы не подчиняется экспоненциальному распределению.
На рис. 1 приведены зависимости изменения Pс( t) и
t) и  с /
с /  (
( t) из которых следует, что:
t) из которых следует, что:
· увеличение кратности резервирования k повышает надежность (Pс возрастает,  с /
с / 
 0);
0);
· резервирование наиболее эффективно на начальном участке работы системы (при t 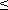 T0), т. е.
T0), т. е.
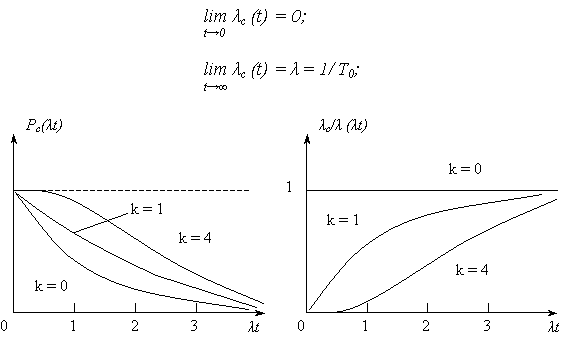
Рис. 10.1
Из графика  с /
с /  (
( t) видно, что при t = (3
t) видно, что при t = (3 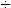 4)T0 = (3
4)T0 = (3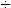 4) 1/
4) 1/  ,
,  с приближается к
с приближается к  .
.
Поскольку средняя наработка до отказа системы при идентичных элементах ( = const):
= const):
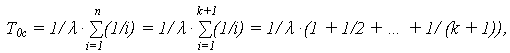
то выигрыш в средней наработке T0с снижается по мере увеличения кратности резервирования.
Например,
при k = 1
T0с = T0 ·(1 + 1/2) = 3/2T0
(увеличение T0с на 50%);
при k = 2
T0с= T0 ·(1 + 1/2 + 1/3) = 11/6T0
(увеличение T0с на 83%);
при k = 3
T0с= 25/12T0
(увеличение T0сна 108%).
Таким образом, динамика роста T0с составляет: 50, 33 и 25%, т. е. уменьшается.
Контрольные вопросы:
1. Чем отличаются системы с нагруженным резервированием с целой и дробной кратностью? Привести расчетные выражения показателей безотказности?
2. Какой закон распределения наработки до отказа будет у системы с нагруженным резервированием, если законы распределения наработки до отказа составляющих ее элементов – экспоненциальные?
3. Какие задачи оптимизации решаются и в чем они состоят для систем с нагруженным резервом?
4. Как определяется вероятность безотказной работы системы с нагруженным резервированием и дробной кратностью?
5. При каких условиях наиболее эффективно применение нагруженного резервирования?
Глава 11.НАДЕЖНОСТЬ СИСТЕМЫ С НЕНАГРУЖЕННЫМ РЕЗЕРВИРОВАНИЕМ
Общий анализ надежности приведен для системы, состоящей из одного основного (рабочего) и (n - 1) резервных элементов.
Допущения:
1. Время замены отказавшего элемента резервным равно 0 (t3  0).
0).
2. Переключающее устройство подключения резервного элемента вместо отказавшего основного – абсолютно надежно.
При ненагруженном резервировании резервный элемент не может отказать, находясь в отключенном состоянии, и его показатели надежности не изменяются.
Исходные данные для расчета надежности:
· вероятность безотказной работы (ВБР) i -го элемента Pi(t).
· интенсивность отказов (ИО) i -го элемента  i(t).
i(t).
· математическое ожидание (МО) наработки до отказа i -го элемента T0i.
Анализ случайной наработки до отказа системы с ненагруженным резервом (рис. 1):
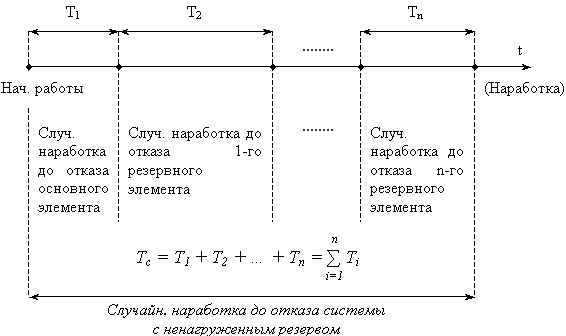
Рис. 11.1
МО наработки до отказа системы:
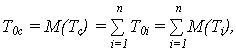
где T0i = M(Ti ) – МО наработки до отказа i -го элемента системы.
Рассмотрим систему, состоящую из основного элемента (ОЭ) и одного резервного (РЭ). ОЭ и РЭ являются невосстанавливаемыми объектами.
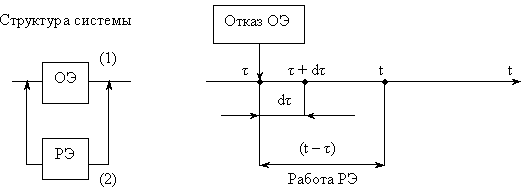
Рис.11.2
События, соответствующие работоспособности системы за наработку (0, t):
A = {безотказная работа (БР) системы за наработку (0, t)};
A1 = {БР ОЭ за наработку (0, t)};
A2 = {отказ ОЭ в момент t > , включение (t3 = 0) РЭ и БР РЭ на интервале (t –
, включение (t3 = 0) РЭ и БР РЭ на интервале (t –  )}.
)}.
Событие A = A1 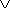 A2, поэтому ВБР системы к наработке t (за наработку (0, t)), определяется:
A2, поэтому ВБР системы к наработке t (за наработку (0, t)), определяется:
P(A) = P(A1 ) + P(A2 ),
где P(A) = Pс(t);
P(A1 ) – ВБР ОЭ к наработке t, P(A1) = P1 (t);
P(A2) = Pр (t) – вероятность отказа ОЭ и БР РЭ после отказа ОЭ.
При известном законе распределения наработка до отказа ОЭ вычисление P1 (t) не представляет сложности.
Событие A2 является «сложным» событием, включающим в себя простые:
A21 = {отказ ОЭ при  < t (вблизи рассматриваемого момента
< t (вблизи рассматриваемого момента  )};
)};
A22 = {БР РЭ с момента  до t, т. е. в интервале (t -
до t, т. е. в интервале (t -  )}.
)}.
Событие A2 осуществляется при одновременном выполнении событий A21 и A22:
A2 = A21 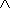 A22.
A22.
События A21 и A22 являются зависимыми, поэтому вероятность события A2
P(A2) = P(A21) · P(A22| A21 ).
Соответствующие вероятности:
1) P(A22| A21 ) = P2 (t -  ) – ВБР РЭ в интервале (t -
) – ВБР РЭ в интервале (t -  ),
),
где P2 (t) – ВБР РЭ к наработке t.
2) для определения P(A21 ) рассмотрен малый интервал ( ,
,  + d
+ d  ), для которого вероятность отказа ОЭ равна:
), для которого вероятность отказа ОЭ равна:
f1( ) d
) d 
Для получения ВО ОЭ к моменту  интегрируем полученное выражение по
интегрируем полученное выражение по  от 0 до t.
от 0 до t.
Поскольку ВО, как функция распределения случайной наработки до отказа,
равна то
то

где 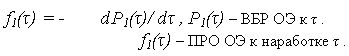
Вероятность события A2:
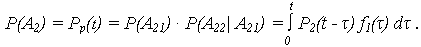
Тогда ВБР рассмотренной системы с ненагруженным резервом равна:

| (1) |
Аналогично, для системы с одним ОЭ и (n -1) РЭ, получается рекуррентное выражение:

| (2) |
где индекс (n - 1) означает, что соответствующие характеристики (ВБР и ПРО) относятся к системе, в которой включается в работу последний n -й элемент.
Выражение (2) приведено для состояния, когда к моменту  отказал предпоследний (n -1) элемент системы и остался лишь один (последний) работоспособный элемент.
отказал предпоследний (n -1) элемент системы и остался лишь один (последний) работоспособный элемент.
Принимая для рассмотриваемой системы, что наработки до отказа ОЭ и РЭ подчиняются экспоненциальному распределению с параметрами  1 и
1 и  2:
2:
P1 (t) = exp (- 1 t); 1 t);
| P2 (t) = exp (- 2 t), 2 t),
|
выражение (1) после интегрирования имеет вид:
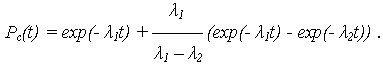
| (3) |
Плотность распределения наработки до отказа системы, равна:
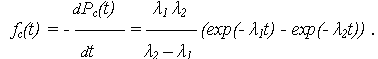
| (4) |
При кратностях резервирования k > 5 распределение наработки до отказа системы с ненагруженным резервом становится близким к нормальному независимо от законов распределения наработки, составляющих систему элементов.
При идентичных ОЭ и (n -1) РЭ и экспоненциальном распределении наработки элементов для ВБР системы с ненагруженным резервом и целой кратностью резервирования k = (n - m)/m, где m = 1:
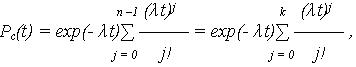
| (5) |
где n – число элементов системы;
k = (n - 1)/1 = (n - 1) – кратность резервирования, при m = 1.
ВО системы:
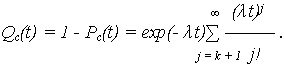
| (6) |
ПРО системы:
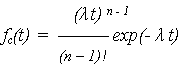
ИО системы:
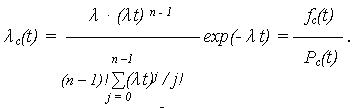
Таким образом, распределение наработки до отказа таких систем подчиняется распределению Эрланга (гамма-распределение при целых n).
Согласно, выражению (5) проанализируем, как изменяется ВБР системы при различной кратности резервирования: 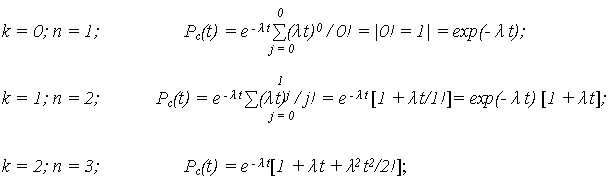
Сравнение ненагруженного и нагруженного резервирований проведено по графику Pс( t) для системы с идентичными элементами (
t) для системы с идентичными элементами ( ) и кратностью резервирования k = 2.
) и кратностью резервирования k = 2.
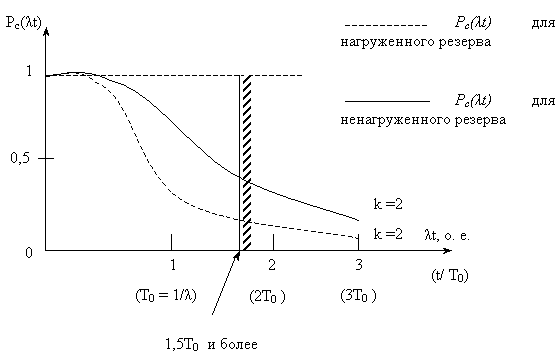
Наибольшая эффективность от использования системы с ненагруженным резервом будет при продолжительности работы РЭ не менее 1.5 T0.
При ненагруженном резерве с дробной кратностью (при m > 1) и экспоненциальном распределении наработки до отказа идентичных элементов (ИО  ) расчетное выражение для Pс(t):
) расчетное выражение для Pс(t):
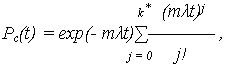
где k* = n – m.
Ниже рассмотрены показатели безотказности системы с ненагруженным резервированием, когда случайная наработка до отказа элементов системы подчиняется нормальному распределению с ПРО
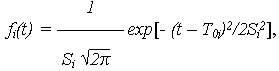
где  - число элементов системы.
- число элементов системы.
Поскольку случайная наработка до отказа системы
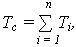
а Ti являются независимыми случайными величинами наработки, то сумма (композиция) независимых случайных величин, каждая из которых распределена нормально, также имеет нормальное распределение с параметрами:
- математическое ожидание наработки до отказа
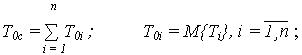
- дисперсия наработки до отказа
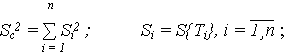
Среднее квадратичное отклонение наработки до отказа системы, определяется:
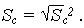
Плотность распределения случайной наработки до отказа системы при целой кратности резервирования
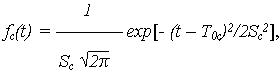
Показатели безотказности определяются с использованием функций f(x) и 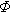 (x) для
(x) для
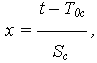
и имеют вид:
Pс(t) = 0,5 - 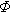 (x); Qс(t) = 0,5 +
(x); Qс(t) = 0,5 + 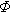 (x).
(x).
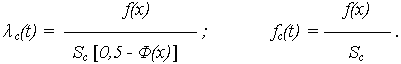
Для системы с элементами наработка на отказ которых подчиняется экспоненциальному распределению Pi (t) = exp(- i t), можно принять Pi(t)
i t), можно принять Pi(t) 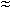 1 -
1 - i t, поэтому выражения ВО и ВБР:
i t, поэтому выражения ВО и ВБР:
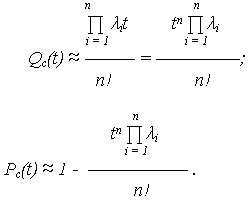
При ненагруженном резерве ВО системы в n! раз меньше, чем при нагруженном.
Контрольные вопросы:
1. Что представляет собой ненагруженное резервирование и как случайная наработка до отказа системы связана со случайными наработками составляющих систему элементов?
2. Основные допущения, принятые при расчете системы с ненагруженным резервированием?
3. К какому закону распределения стремится наработка до отказа системы при больших значениях кратности резервирования?
4. Проанализируйте, как изменяется вероятность безотказной работы системы с увеличением кратности резервирования?
5. При каких условиях ненагруженное резервирование становится значительно эффективнее нагруженного?
6. Какой закон распределения наработки до отказа будет у системы с ненагруженным резервированием, если законы распределения наработки до отказа элементов являются нормальными?
7. Приведите расчетные формулы показателей безотказности для системы с нормальным распределением наработки элементов?
Глава 12. НАДЕЖНОСТЬ СИСТЕМ С ОБЛЕГЧЕННЫМ И СО СКОЛЬЗЯЩИМ РЕЗЕРВОМ
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 7195; Нарушение авторских прав?; Мы поможем в написании вашей работы!