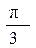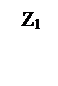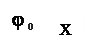КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И тригонометрической формах
|
|
|
|
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ
Комплексные числа считаются равными, если равны соответственно их действительные и мнимые части. У равных комплексных чисел модули равны, а аргументы совпадают с точностью до слагаемого 2pк. Понятия «больше» и «меньше» для комплексных чисел смысла не имеют.
Сложение и вычитание комплексных чисел Z1 = a 1 + i b 1 и Z2 = a 2+ i b 2
(т. е. в алгебраической форме) производится следующим образом:
Z1 ± Z2 = (a 1 + i b 1) ± (a 2 + i b 2) = (a 1 ± a 2) + i (b 1 ± b 2).
Пример 1.
a) (4 + i 2) + (1 + i5) = (4 + 1) + i (2 + 5) = 5 + i 7.
b) (3 + i 5) – (6 + i З) = (3 – 6) + i (5 – 3) = – 3 + i 2.
Важно отметить, что результатом сложения комплексно-сопряжённых чисел оказывается действительное число, а результатом вычитания – мнимое.
Векторная трактовка геометрического смысла комплексных чисел позволяет особенно наглядно пояснить приведённые выше положения о сравнении комплексных чисел и правилах их сложения и вычитания. Так, например, сумма двух комплексных чисел Z1 = 4 + i 2 и Z2 = 1 + i 5 представляется суммой векторов, изображающих отдельные слагаемые
(см. рис. 4).

|
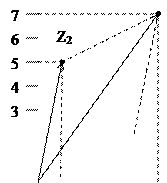 |



|







 |
| |||
Разность двух комплексных чисел Z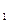 = 3 + i5 и Z
= 3 + i5 и Z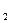 = 6 + iЗ представ
= 6 + iЗ представ
ляется разностью векторов, изображающих отдельные слагаемые (как показано на рис. 5).
|
|
|




|

 |
|
|
|











|
Рис. 5
Перемножив комплексные числа Z1 = a 1 + i b 1 и Z2 = a 2 + i b 2 по правилу перемножения многочленов (с учётом i2 = – 1), получим:
(а 1 + i b 1)  (а 2+ i b 2) = а 1 а 2 + а 1 i b 2 + i b 1 а 2 + i b 1 i b 2 =
(а 2+ i b 2) = а 1 а 2 + а 1 i b 2 + i b 1 а 2 + i b 1 i b 2 =
= (а 1 а 2 – b 1 b 2) + i (а 1 b 2 + b 1 а 2)
Пример 2.
(3 + i)(5 - i2) = [3  5 – 1
5 – 1 (– 2)] + i [3(–2) + 1
(– 2)] + i [3(–2) + 1 5] = 17 – i.
5] = 17 – i.
Важно отметить, что произведение комплексно-сопряжённых чисел
Z = а + i b и 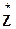 = а – i b даёт сумму квадратов их действительной и мнимой частей:
= а – i b даёт сумму квадратов их действительной и мнимой частей:
(а + i b)(а – i b) = а 2 + b 2 (21)
Деление комплексных чисел осуществляется следующим образом:
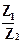 =
= 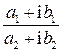 =
= 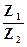 ∙
∙ 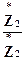 =
= 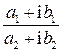 ∙
∙ 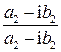 =
=
= 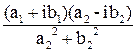 =
= 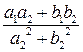 + i
+ i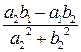 . (22) Пример 3.
. (22) Пример 3.
Разделить число (3 – i 2) на число (– 4 + i).
Решение:
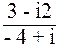 =
= 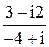 ∙
∙ 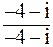 =
=
= 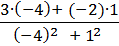 + i
+ i 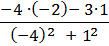 = –
= – 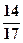 + i
+ i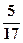 .
.
Производить умножение и деление комплексных чисел в тригонометрической форме удобнее, чем в алгебраической.
Пусть Z1 = | Z1 | (cos φ1+ i sin φ1 ), Z2 = | Z2 | (cos φ2+ i sin φ2 ).
Тогда Z1 ∙ Z2 = | Z1 |∙| Z2 | [(cos φ1 ∙ cos φ2 - sin φ1 ∙ sin φ2) +
+ i (sin φ1 ∙ cos φ2 + cos φ1 ∙ sin φ2)] =
= | Z1 || Z2 | [cos (φ1 + φ2) + i sin (φ1 + φ2 )]. (23)
Эта формула легко обобщается на случай умножения n комплексных чисел
Z1 · Z2 ·... · Zn =
= | Z1 |·| Z2 | …·| Zn |[(cos (φ1 + φ2 +...+ φn) + i sin (φ1 + φ2 +...+ φn)]. (24)
| Отсюда: |
| Z1 · Z2 ·...· Zn| = | Z1 |·| Z2 |·... ·| Zn |. (25)
arg (Z1 · Z2 ·...· Zn) = arg Z1 + arg Z2 +... + arg Zn. (26)
Таким образом, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Пример 4. [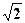 (cos
(cos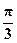 + i sin
+ i sin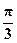 )][
)][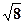 (cos
(cos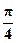 – i sin
– i sin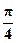 )] =
)] =
= 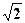 [ cos
[ cos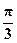 + i sin
+ i sin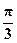 ]
]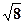 [ cos (–
[ cos (–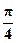 ) + i sin (–
) + i sin (–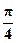 )] =
)] =
=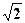
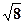 [cos(
[cos(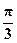 –
–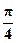 ) + i sin(
) + i sin(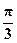 –
–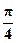 )] = 4(cos
)] = 4(cos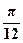 +i sin
+i sin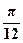 ).
).
Рассмотрим операцию умножения комплексных чисел с геометрической точки зрения. Сложение и вычитание комплексных чисел геометрически иллюстрируется как сложение и вычитание соответствующих векторов. Для
умножения и деления такой простой геометрической иллюстрации (с помощью соответствующих векторов) не получается. Зато можно легко дать геометрическую иллюстрацию умножения и деления комплексных чисел в тригонометрической форме.
При умножении чисел Z1 = | Z1 | (cos φ+ i sin φ) и Z2 = 3(cos 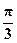 + i sin
+ i sin 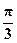 )
)
модуль вектора, соответствующего произведению Z1·Z2, получается из модуля вектора, соответствующего числу Z1, растяжением последнего в три раза и поворотом на угол 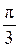 (рис. 6).
(рис. 6).
|
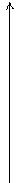
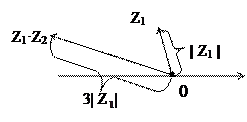 |
X
Рис. 6
Растяжение и поворот вектора при умножении обладают перемести-тельным свойством.
Чтобы комплексное число, заданное в тригонометрической форме, возвести в целую степень, достаточно модуль числа возвести в эту степень, а аргумент умножить на показатель степени:
Zn = | Z |n [cos(nφ)+ i sin(nφ)], (27)
т. е.
| Zn | = | Z |n и arg Zn = n·arg Z
(–1 + i)6 = [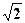 (cos 135° + i sin 135°)]6 =
(cos 135° + i sin 135°)]6 =
= (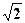 )6 (cos 810°+ i sin 810°) = 8[cos(90° + 360°·2)+
)6 (cos 810°+ i sin 810°) = 8[cos(90° + 360°·2)+
+ i sin(90° + 360° · 2)] = 8[cos 90° + i sin 90°] =
= 8(0 + 1i) = 8i.
В частном случае при | Z | = 1 (cos φ + i sin φ)n =cos (n φ) + i sin (n φ) (28)
Равенство (28) называется формулой Муавра[13]. Используя формулу Муавра (28), формулу бинома Ньютона (1) и условие равенства комплексных чисел, можно получать формулы для косинуса и синуса кратных углов. Например, по формуле бинома Ньютона:
(cos φ + i sin φ)3 = cos3 φ + 3 cos2 φ i sin φ – 3 cos φ sin2 φ –
– i sin3 φ = (cos3 φ – 3cos φ sin2 φ) + i(3cos2 φ sin φ – sin3 φ),
а по формуле Муавра:
(cos φ + i sin φ)3 = cos (3φ) + i sin(3φ).
Сравнивая результаты двух предыдущих вычислений, получим
cos Зφ + i sin 3φ = (cos3φ – 3cos φ sin2 φ) + i(3 cos2 φ sin φ – sin3 φ).
По условию равенства комплексных чисел находим формулы тройных углов для косинуса и синуса: cos 3φ = cos3 φ – 3cos φ sin2φ
sin 3φ = 3 cos2 φ sin φ – sin3 φ.
Деление комплексных чисел в тригонометрической форме осуществляется следующим образом:
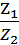 =
= 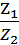
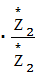 =
= 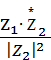 =
=
= 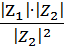
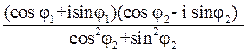 =
=
= 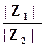 [cos(φ1 – φ2) + i sin(φ1– φ2)]. (29)
[cos(φ1 – φ2) + i sin(φ1– φ2)]. (29)
Т. е. модуль результата деления равен 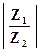 =
= 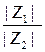 (30),
(30),
а аргумент Arg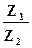 = Arg Z1 – Arg Z2 = arg Z1– arg Z2 + 2pk, (31).
= Arg Z1 – Arg Z2 = arg Z1– arg Z2 + 2pk, (31).
Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, модуль делимого делится на модуль делителя, и из аргумента делимого вычитается аргумент делителя.
Делению комплексных чисел можно дать геометрическую интерпретацию, аналогичную интерпретации действия умножения, а именно: при делении одного комплексного числа на другое комплексное число, модуль вектора, соответствующий делимому, сжимается в число раз, равное модулю делителя, а сам вектор поворачивается в отрицательном направлении на угол, равный аргументу делителя.
Действие извлечения корня n-й степени из комплексного числа
Z = | Z |(cos θ + i sin θ)
адекватно возведению этого комплексного числа в степень 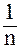 :
:
w = 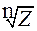 = | Z |
= | Z |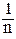 (cos
(cos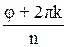 + i sin
+ i sin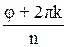 ). (32)
). (32)
Полагая в формуле (32) k = 0,1, 2,..., (n – 1). Получим n различных значений φ0, φ1,...., φ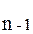
 аргумента w. Все остальные возможные значения аргумен-та будут отличаться от перечисленных на числа, кратные 2p.
аргумента w. Все остальные возможные значения аргумен-та будут отличаться от перечисленных на числа, кратные 2p.
Важные замечания:
1. Если во всех предыдущих примерах с действиями над комплексными числами запись аргументов в виде θ или φ была несущественной, то при извлечении корня из комплексного числа его аргумент следует обязательно писать в форме θ = φ + 2pk.
2. При извлечении корня из модуля впереди ставится знак «+», т.к. корень любой степени из модуля – всегда величина неотрицательная.
3. Если 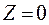 , значение Arg Z не определено, а при
, значение Arg Z не определено, а при 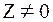 оно определено с точностью до величины, кратной
оно определено с точностью до величины, кратной 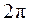 .
.
Пример 6.
Найти комплексное число w = 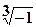 .
.
Решение:
Т. к. – 1 = cos p + i sin p, то
w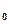 =
= 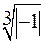 (cos
(cos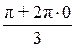 + i sin
+ i sin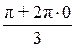 ) =
) = 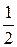 + i
+ i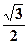 .
.
w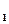 =
= 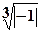 (cos
(cos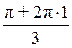 + i sin
+ i sin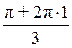 ) = cos p + i sin p = –1.
) = cos p + i sin p = –1.
w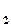 =
= 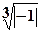 (cos
(cos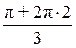 + i sin
+ i sin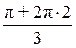 ) = cos
) = cos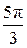 + i sin
+ i sin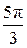 =
= 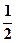 – i
– i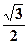 .
.
Равенство (28) показывает, что модули всех корней одинаковы, а главные значения аргументов отличаются на числа, кратные 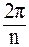 . Отсюда виден способ геометрического решения задачи извлечения корня из комплексного числа. Для этого надо найти точки w
. Отсюда виден способ геометрического решения задачи извлечения корня из комплексного числа. Для этого надо найти точки w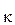 (k = 0,1,..., n – 1), расположенные в вершинах правильного n-угольника, вписанного в окружность радиуса
(k = 0,1,..., n – 1), расположенные в вершинах правильного n-угольника, вписанного в окружность радиуса 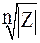 . Для построения w0 достаточно найти на этой окружности точку, для которой arg w0 =
. Для построения w0 достаточно найти на этой окружности точку, для которой arg w0 = 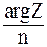 = φ0. Полярные углы всех остальных точек можно получить последовательными поворотами полярного радиуса 0w0 на угол
= φ0. Полярные углы всех остальных точек можно получить последовательными поворотами полярного радиуса 0w0 на угол 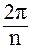 .
.

|
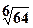 .
.
 |
Рис. 7.
§ 4. ПРИМЕР РЕШЕНИЯ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ ВИДА Zn+ а = 0
Найдём все корни уравнения
Z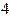 + a = 0, где a =
+ a = 0, где a = 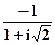 .
.
Перепишем исходное уравнение в виде
Z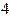 =
= 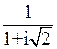 .
.
В правой части осуществим деление комплексных чисел (1 + i 0) и (1 + i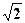 ) в алгебраической форме по формуле (22):
) в алгебраической форме по формуле (22):
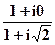 =
=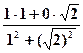 + i
+ i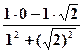 =
=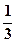 – i
– i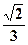 .
.
Перейдём к тригонометрической форме по формулам (11) – (13):
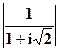 =
= 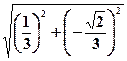 =
= 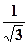 =
= 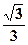 ,
,
cos φ =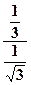 =
= 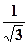 ; sin φ = –
; sin φ = –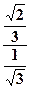 = –
= –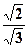 = –
= –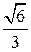 ,
,
т. к. cos φ > 0 и sin φ < 0, то φ – угол четвёртой четверти.
Зададимся точностью конечного результата в 0,01, это значит, что в промежуточных расчётах необходимо иметь три знака после запятой.
Arg Z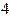 = arccos
= arccos 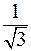 + 2pk» 0, 955 + 2pk,
+ 2pk» 0, 955 + 2pk,
Z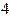 =
= 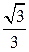 [cos(– 0,955 + 2pk) + i sin(– 0,955 + 2pk)],
[cos(– 0,955 + 2pk) + i sin(– 0,955 + 2pk)],
Z = 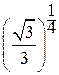 (cos
(cos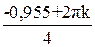 + i sin
+ i sin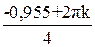 ) =
) =
= 0,872[cos(– 0,239 + 1, 571·k) + i sin(– 0,239 + 1,571·k)]
Z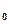 = 0,872[cos(– 0,239) + i sin(– 0,239)] = 0, 872[0,972 + i (– 0,237)] =
= 0,872[cos(– 0,239) + i sin(– 0,239)] = 0, 872[0,972 + i (– 0,237)] =
= 0,848 – i 0,207» 0,85 – i 0,21
Здесь целесообразно напомнить, что аргументы синуса и косинуса измерялись в радианной мере. Чтобы вычислить значение аргумента φ0 в градусной мере, необходимо воспользоваться соотношением
φ0 = 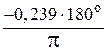 » –13, 7
» –13, 7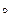 .
.
Итак, модуль каждого из четырёх корней уравнения равен 0,87, а разница ∆φ между аргументами корней составляет
∆ φ = 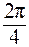 = 90
= 90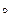 .
.
Геометрическое решение имеет вид, представленный на рис. 8
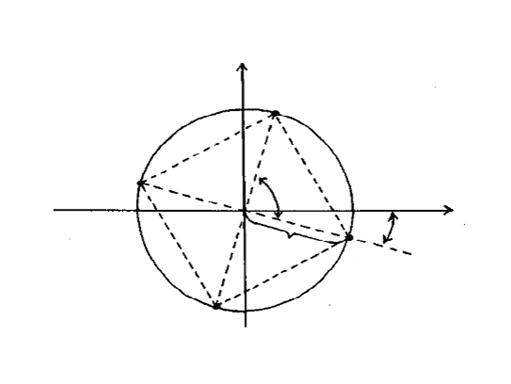 |
Рис. 8
Геометрическое решение даёт наглядную картину распределения корней на комплексной плоскости, но не является точным, поэтому требуется аналитическое решение поставленной задачи:
Z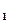 = 0,872[cos(– 0,239 + 1,571·1) + i sin(– 0,239 + 1,571·1)] =
= 0,872[cos(– 0,239 + 1,571·1) + i sin(– 0,239 + 1,571·1)] =
= 0,965[cos 1,332 + i sin1,332] = 0,872(0,237 + i 0,972) = 0,207 + i 0,848»
» 0,21 + i 0,85.
Z2= 0, 872[cos(– 0,239 + 1,571·2) + i sin(– 0,239 + 1,571·2)] =
= 0, 872[cos 2,903 + i sin 2,903] = 0, 872(– 0,972 + i 0,236)»
» – 0,848 + i 0,206» – 0,85 + i 0,21.
Z3 = 0, 872[cos(– 0,239 + 1,571· 3) + i sin(– 0,239 + 1,571· 3)] =
= 0, 872[cos4, 474 + i sin4,474] = 0,872[– 0,236 + i (- 0,972)] =
= – 0,206 – i 0,848» – 0,21 – i 0,85.
Итак,
Z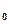 » 0,85 – i 0,21
» 0,85 – i 0,21
Z1» 0, 21 + i 0,85.
Z2» – 0, 85 + i 0,21.
Z3» – 0, 21 – i 0,85.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 624; Нарушение авторских прав?; Мы поможем в написании вашей работы!