
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показательная форма комплексного числа
|
|
|
|
Рассмотрим некоторые свойства экспоненциальной функции
f (x) = e а х.
Пусть f(x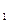 ) = е a x
) = е a x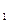 и f(x2) = е а х
и f(x2) = е а х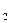 .
.
Тогда
f(x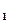 ) f(x
) f(x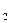 ) = e a x
) = e a x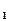 ·е а х
·е а х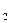 = e
= e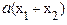 . (33)
. (33)
Известно, что
(е а х)´ = а ·е а х, (34)
т. е. экспоненциальная функция обладает следующими двумя свойствами:
f(x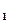 )·f(x
)·f(x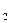 ) = f(x
) = f(x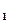 + x
+ x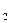 ), (35)
), (35)
f´(x) = а ·е а х = a ·f x).
Теперь рассмотрим функцию:
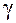 (φ) = cos φ + i sin φ (36)
(φ) = cos φ + i sin φ (36)
Убедимся, что она обладает теми же свойствами:
(cos φ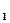 + i sin φ
+ i sin φ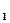 ) (cos φ 2 + i sin φ 2) =
) (cos φ 2 + i sin φ 2) =
= cos φ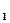 · cos φ 2 + cos φ
· cos φ 2 + cos φ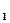 · i sin φ 2 + i sin φ
· i sin φ 2 + i sin φ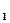 ·cos φ 2 + i sin φ
·cos φ 2 + i sin φ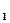 · i sin φ 2 =
· i sin φ 2 =
= cos(φ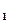 + φ 2) + i sin(φ
+ φ 2) + i sin(φ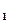 + φ 2). (37)
+ φ 2). (37)
(cos φ + i sin φ)´ = – sin φ + i cos φ =
= 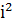 sin φ + icos φ = i (cos φ + i sin φ). (38)
sin φ + icos φ = i (cos φ + i sin φ). (38)
Полагая а = i, можем считать, что функции eiφ и 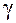 (φ) ведут себя одинаково, т. е. можно считать:
(φ) ведут себя одинаково, т. е. можно считать:
eiφ = cos φ + i sin φ (39)
Это равенство называется формулой Эйлера[14].
Пользуясь формулой Эйлера, можно представить комплексное число
в тригонометрической форме
Z = а + i b = |Z| (cos φ + i sin φ)
и в показательной форме:
Z = |Z| ei argZ = ρeiφ (40)
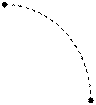
Чтобы по выражению (40) найти на комплексной плоскости точку, соответствующую числу Z, достаточно отложить от начала координат на действительной оси отрезок величиной |Z| и повернуть его вокруг центра координат на угол φ в положительном направлении (рис.9)
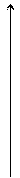
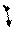

 Y
Y
|
 0 X
0 X
|Z|
Рис. 9
Поэтому множитель eiφ иногда называют оператором поворота.
В частности,
1 = е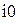 ; i = е
; i = е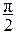 ; – 1 = e
; – 1 = e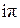 ; – i = e
; – i = e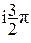
Аргумент комплексного числа является естественным обобщением знака действительного числа. В самом деле, аргументы положительных и отрицательных чисел равны соответственно 0 и p.
Рассмотрим примеры умножения и деления комплексных чисел в показательной форме.
Пример 1.
(7e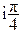 )(0,5e
)(0,5e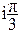 ) = 7· 0,5
) = 7· 0,5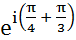 = 3,5
= 3,5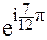
Здесь сразу видны полярные координаты (3,5; 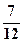 p) результата перемно-жения.
p) результата перемно-жения.
Пример 2.
(6e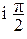 ): (2e
): (2e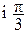 ) =
) = 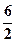 e
e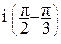 = 3e
= 3e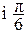 .
.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 904; Нарушение авторских прав?; Мы поможем в написании вашей работы!