Понятие о числе Рейнольдса

Формула Пуазейля. Ламинарное и турбулентное течение жидкости.

Течение вязкой жидкости по цилиндрическим трубам.

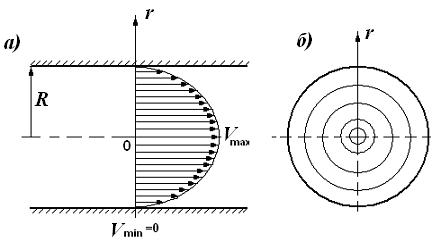Жидкость, протекающую по цилиндрической трубе радиуса R, можно представить разделенной на концентрические слои (рис.10).

Рис.10

В каждом таком слое скорость течения постоянна, но от слоя к слою изменяется. Слой, прилипший к стенкам трубы, имеет скорость, равную нулю, V _min=0. Слой, текущий вдоль оси трубы, имеет максимальную скорость V _max. Профиль скорости в этом случае является параболой (рис.10, а). Вдоль радиуса трубы (ось r) скорость изменяется, и это изменение характеризуется величиной .

Задача о течении вязкой жидкости по цилиндрическим трубам имеет исключительно важное значение для физиологии, так как кровеносная система является системой из многократно разветвляющихся цилиндрических сосудов различных диаметров.

Важнейшую закономерность течения вязкой жидкости по цилиндрическим трубам представляет формула Пуазейля, позволяющая рассчитать объем жидкости, протекающий через поперечное сечение трубы за одну секунду:

,

где - объем жидкости, протекающей через поперечное сечение трубы 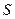за время. Используя формулу (1), можно записать

,

где - средняя скорость течения жидкости в трубе. Тогда, учитывая, что S=запишем Q =.

Для вычисления выделим в объеме текущей жидкости малый цилиндр произвольного радиуса r длиной l (рис.11). Обозначим давление в жидкости слева от выбранного цилиндра через Р ₁, а справа - через Р ₂. На малый цилиндр в потоке действуют две силы: _1, обусловленная разностью давлений - Р ₂, сообщающая цилиндру ускорение, и сила - сила трения (вязкости), которую испытывает этот цилиндр, перемещаясь в потоке жидкости.

Рис.11

Для силы F ₁ запишем

F ₁=

где S₁= - площадь поперечного сечения малого цилиндра.

Используя формулу Ньютона, для силы F ₂ получим:

F ₂ =,

где S ₂ = 2боковая поверхность малого цилиндра (поверхность соприкосновения этого цилиндра с остальным объемом жидкости).

Чтобы цилиндр двигался с постоянной скоростью, надо чтобы силы и уравновешивали друг друга, т.е. должно выполняться условие

. (15)

Условие (15) через модули сил запишем в виде F ₁=- F ₂ или, подставив значение сил, получим

(Р ₁- Р ₂)= - . (16)

Произведем сокращения и выразим из этого уравнения :

_.

Проинтегрируем полученное уравнение, подставив предел интегрирования:

,

или _. (17)

На осевой линии трубы r =0, а скорость , тогда (17) можно переписать в виде 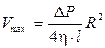. (18)

Формула (18) была получена французским физиком и физиологом Пуазейлем в 1841 году. Из (18) видно, что максимальная скорость течения жидкости по трубе прямо пропорциональна перепаду давления квадрату радиуса трубы R и обратно пропорциональна коэффициенту вязкости 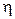жидкости и длине цилиндра l. Подставляя (18) в (14),получим Q =, или в окончательном виде

  (19)

Q =.

Полученное выражение носит название формулы Гагена - Пуазейля, или формулы Пуазейля.

Таким образом, объем жидкости Q, ежесекундно протекающей через поперечное сечение трубы, прямо пропорционален четвертой степени радиуса трубы R (Q~R ⁴), разности давлений и обратно пропорционален коэффициенту вязкости и длине трубы .

Часто проводят аналогию между формулой Пуазейля и законом Ома для однородного участка цепи (сила тока прямо пропорциональна разности потенциалов на участке цепи и обратно пропорциональна сопротивлению R этого участка.) Формулу (19) представим в виде

Q =.

Величину С =называют гидравлическим сопротивлением. Оно тем больше, чем больше вязкость жидкости 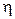и длина трубы l, и зависит обратно пропорционально от четвёртой степени радиуса трубы R.

Таким образом, объём жидкости, ежесекундно протекающей через поперечное сечение трубы, прямо пропорционален разности давлений и обратно пропорционален гидравлическому сопротивлению С.

Аналогия между сопротивлением в электрической цепи и гидравлическим сопротивлением позволяет использовать правила для расчета сопротивления при последовательном и параллельном соединении труб с различными сопротивлениями.

Общее гидравлическое сопротивление труб, соединённых последовательно, рассчитывается по формуле

С=С₁+С₂+С₃+…,

а соединённых параллельно - по формуле

.

Формула Пуазейля справедлива не для любого течения вязкой жидкости, а только для ламинарного течения.

В гидродинамике различают два вида течения жидкости – ламинарное и турбулентное.

Рис.12

Ламинарным называют слоистое течение, при котором слои не перемешиваются друг с другом. Для цилиндрического профиля трубы профиль скорости такого течения дан на рис.10,а.

Турбулентным называют течение, при котором происходит интенсивное перемешивание слоёв, образуются завихрения жидкости.

Турбулентность увеличивает гидравлическое сопротивление. Профиль скорости такого движения в цилиндрической трубе показан на рис.12.Вблизи стенок трубы наблюдается большой перепад скорости, скорость быстро нарастает от 0 до V – некоторого среднего значения скорости частиц, что позволяет считать такое течение в среднем однородным.

Характер течения жидкости (ламинарное или турбулентное) определяется целым рядом факторов: вязкостью жидкости, сечением трубы, скоростью течения и плотностью жидкости.

Как уже рассматривалось выше, на любой малый объём жидкости в потоке действуют ускоряющая сила и сила вязкого трения . Характер течения будет определяться отношением 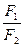. Чем больше это отношение, тем больше вероятность возникновения вихрей, а следовательно, и турбулентного течения. Английский физик и инженер Рейнольдс рассчитал безразмерное отношение F ₁/ F ₂. Это отношение получило название числа Рейнольдса Re. Очевидно, число Re есть величина безразмерная:

=, (20)

где плотность жидкости, l –характерный линейный размер сечения трубы (диаметр или радиус для цилиндрического сечения трубы, высота – для треугольного, сторона – для квадратного), скорость потока, коэффициент вязкости.

Так как число Рейнольдса зависит от двух характеристик жидкости – вязкости 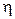и плотности , то целесообразно ввести в это число величину называемую кинематической вязкостью. Тогда (20) принимает вид

.

Переход от ламинарного течения к турбулентному определяется критическим числом Рейнольдса.

При числах течение носит ламинарный характер, при > течение становится турбулентным. Критические значения числа Рейнольдса определяются только экспериментально. Для гладких цилиндрических труб 1000, если за принять радиус трубы. Число Рейнольдса играет большую роль во многих количественных исследованиях течения жидкости и газа. Оно является критерием подобия при создании моделей гидро- и аэродинамических систем и, в частности, кровеносной системы. Важно, чтобы модель имела то же число Рейнольдса, что и сама система. Это достигается соответствующим подбором скорости, вязкости и линейного размера сечения модели. Из (20) видно, что увеличение размеров сечения можно скомпенсировать уменьшением скорости течения или подбором жидкости с соответствующими значениями вязкости 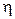и плотности .

Течение крови в сосудах носит в норме ламинарный характер, небольшая турбулентность наблюдается вблизи клапанов сердца. При патологии число Re может превысить критическое значение и течение станет турбулентным, что можно обнаружить по характерным шумам и использовать в диагностике заболеваний.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Дата добавления: 2014-10-15